電験一種 R6年 電力・管理 問4
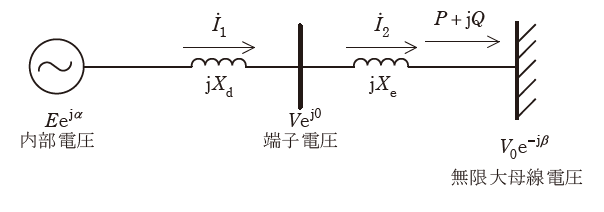
図に示す1機無限大母線系統において、発電所から無限大母線へと送電することを考える。発電機の内部電圧と端子電圧をそれぞれ\(E e^{j\alpha}\)及び\(V e^{j0}\)、無限大母線の電圧を\(V_0 e^{-j\beta}\)、発電機の同期リアクタンスを\(X_d\)、送電線のリアクタンスを\(X_e\)とする(ただし、\(\alpha > 0\)、\(\beta > 0\)とする)。無限大母線での受電電力を\(P + jQ\)とする(ただし\(P > 0\)、\(Q\)は遅れを正とする)。送電線の抵抗や静電容量は無視して良い。全ての変数は共通の基準値による単位法表現とし、以下の問に答えよ。なお、同期化力が0以上である場合には小じょう乱同期安定性(定態安定度)の観点から安定な送電は可能とする。
(1) 無限大母線の受電電力\(P\)及び\(Q\)を、それぞれ\(E\)、\(V_0\)、\(\alpha\)、\(\beta\)、\(X_d\)、\(X_e\)を用いて表せ。
(2) 同期化力により定まる小じょう乱同期安定性の観点から、安定な送電のために\(\alpha + \beta\)が満たすべき条件を示せ。
(3) 図の\(jX_d\)を流れる電流\(\dot{I_1}\)を、\(E\)、\(V\)、\(\alpha\)、\(X_d\)を用いて表せ。同様に、\(jX_e\)を流れる電流\(\dot{I_2}\)を、\(V\)、\(V_0\)、\(\beta\)、\(X_e\)を用いて表せ。
(4) 小問(2)で示した小じょう乱同期安定限界において\(V = V_0\)であるとき、発電機の内部電圧\(E\)を\(V_0\)、\(X_d\)、\(X_e\)を用いて表せ。ここで、\(\dot{I_1} = \dot{I_2}\)であり、かつ複素数\(a + jb = c\)(\(a\), \(b\), \(c\)は実数)について\(a^2 + b^2 = c^2\)が成立することを用いよ。
(5) \(V = V_0\)かつ\(X_e = \dfrac{1}{2} X_d\)のとき、安定に送電できる有効電力の最大値を\(V_0\)と\(X_d\)を用いて表せ。ただし、小じょう乱同期安定性以外の制約条件は無視せよ。
出典:令和6年度第一種電気主任技術者電力・管理科目問4
解説
計算に時間を要するため、他の問題を解いた後に残った時間でどこまで解けるかという問題じゃないかなと思います。
この手の問題は時間は要するものの、過去問と似たような問題ではあるので計算重視でいくのであれば選択すべきであると考えます。
標準解答と補足
(1) 無限大母線に向かう電流\(\dot{I}_2\)は、内部電圧と無限大母線の間の電位差を、直列インピーダンス\(j(X_d + X_e)\)で除することで次式により表される。
\(\dot{I}_2 = \dfrac{E e^{j\alpha} - V_0 e^{-j\beta}}{j(X_d + X_e)}\)
無限大母線の受電電力は、\(P + jQ = V_0 e^{-j\beta} \bar{\dot{I_2}}\)より以下のとおり表せる。
\begin{eqnarray} \left\{ \begin{array}{l} P = \dfrac{EV_0}{X_d + X_e} \sin(\alpha + \beta) \\ Q = \dfrac{EV_0}{X_d + X_e} \cos(\alpha + \beta) - \dfrac{V_0^2}{X_d + X_e} \end{array} \right. \quad \cdots (\text{答}) \end{eqnarray}
補足
\(P+jQ\)の計算過程を示します。
\begin{aligned} P + jQ &= V_0 e^{-j\beta} \bar{\dot{I_2}} \\ &= (V_0 e^{-j\beta}) \left\{ \frac{Ee^{-j\alpha} - V_0e^{j\beta}}{-j(X_d + X_e)} \right\} \\ &= \frac{V_0 e^{-j\beta} (V_0e^{j\beta} - Ee^{-j\alpha})}{j(X_d + X_e)} \\ &= \frac{V_0^2 e^{-j\beta}e^{j\beta} - V_0 E e^{-j\beta}e^{-j\alpha}}{j(X_d + X_e)} \\ &= \frac{V_0^2 - V_0 E e^{-j(\alpha + \beta)}}{j(X_d + X_e)} \\ &= \frac{V_0^2 - V_0 E \left\{ \cos(\alpha + \beta) - j\sin(\alpha + \beta)\right\} }{j(X_d + X_e)} \\ &= \frac{-jV_0^2 + jV_0 E \cos(\alpha + \beta) + V_0 E \sin(\alpha + \beta)}{(X_d + X_e)} \\ &= \frac{ E V_0}{X_d + X_e} \sin(\alpha + \beta) + j \left\{ \frac{ E V_0 }{X_d + X_e} \cos(\alpha + \beta) - \frac{ V_0^2 }{X_d + X_e} \right\} \\ \end{aligned}
(2) \(\alpha + \beta = \delta\)とおくと、同期発電機の有効電力出力(損失が無いので小問(1)で導出した\(P\)と同じ)を\(\delta\)で微分することで、同期化力を次式の通り導出できる。
\(\dfrac{dP}{d\delta} = \dfrac{EV_0}{X_d + X_e} \cos(\alpha + \beta)\)
小じょう乱同期安定性の観点からは、同期化力が正の値若しくは0であることが必要なので、\(\alpha + \beta\)が満たすべき条件は次式となる。
\(0 < \alpha + \beta \leqq \dfrac{\pi}{2}\) ・・・(答)
補足
損失が無いのは送電線の抵抗を無視していることから有効電力の消費がないためです。
\(0 < \alpha + \beta\)となっているのは、題意より\(\alpha > 0 \)、\( \beta > 0 \)であるためです。
おそらくここは\(0 \leqq \alpha + \beta\)としても大きな減点はない気がします。
(3) \(\dot{I}_1\)及び\(\dot{I}_2\)は、それぞれリアクタンス両端の電位差をインピーダンスで除して、次式の通り表せる。
\begin{eqnarray} \left\{ \begin{array}{l} \dot{I}_1 = \dfrac{E e^{j\alpha} - V}{jX_d} \\ \dot{I}_2 = \dfrac{V - V_0 e^{-j\beta}}{jX_e} \\ \end{array} \right. \quad \cdots (\text{答}) \end{eqnarray}
三角関数を用いた場合は次式の通り(\(e\)を用いた表現といずれも可)。
\begin{eqnarray} \left\{ \begin{array}{l} \dot{I}_1 = \dfrac{E \cos \alpha - V + j E \sin \alpha}{jX_d} \\ \dot{I}_2 = \dfrac{V - V_0 \cos \beta + j V_0 \sin \beta}{jX_e} \\ \end{array} \right. \end{eqnarray}
補足
試験では他の問題の解答状況にもよりますがここまでできれば及第点かと思います。
(4) 小じょう乱同期安定限界では、小問(2)より次式が成立する。
\(\alpha + \beta = \dfrac{\pi}{2}\)
ここで題意より\(V = V_0\)とすると、発電機の同期リアクタンスと送電線のリアクタンスを流れる電流\(\dot{I}_1\)と\(\dot{I}_2\)は、それぞれ次式の通り表せる。
\begin{eqnarray} \left\{ \begin{array}{l} \dot{I}_1 = \dfrac{E e^{j\alpha} - V_0}{jX_d} \\ \dot{I}_2 = \dfrac{V_0 - V_0 e^{-j\beta}}{jX_e} \\ \end{array} \right. \end{eqnarray}
この両者が等しい条件から次式が成立する。
\begin{aligned} \dfrac{E e^{j\alpha} - V_0}{jX_d} = \dfrac{V_0 - V_0 e^{-j\beta}}{jX_e} \\ \end{aligned}
上式を整理して次式を得る。
\((X_e E \cos \alpha + X_d V_0 \cos \beta) + j (X_e E \sin \alpha - X_d V_0 \sin \beta) = (X_e + X_d) V_0\)
ここで、\(\alpha + \beta = \dfrac{\pi}{2}\)より\(\cos \beta = \sin \alpha\)及び\(\sin \beta = \cos \alpha\)が成立するため、以下のとおり展開できる。
\begin{aligned} (X_e E \cos \alpha + X_d V_0 \sin \alpha ) + j (X_e E \sin \alpha - X_d V_0 \cos \alpha) &= (X_e + X_d) V_0\\ (X_e E \cos \alpha + X_d V_0 \sin \alpha ) ^2+ (X_e E \sin \alpha - X_d V_0 \cos \alpha)^2 &= (X_e + X_d)^2 V_0^2\\ X_e^2 E^2 + X_d^2 V_0^2 &= (X_e + X_d)^2 V_0^2\ \end{aligned}
以上より、\(E = \sqrt{1 + \dfrac{2 X_d}{X_e}} V_0\) ・・・(答)
補足
\(\cos \beta = \sin \alpha\)について
\begin{aligned} \cos \beta &= \cos \left( \frac{\pi}{2} - \alpha \right) \\ &= \cos \frac{\pi}{2} \cos \alpha + \sin \frac{\pi}{2} \sin \alpha \\ &= \sin \alpha \\ \end{aligned}
念のため。
(5) 発電機出力は小問(1)より次式で表される。
\(P = \dfrac{E V_0}{X_d + X_e} \sin (\alpha + \beta)\)
ここで、小じょう乱同期安定限界では\(\alpha + \beta = \dfrac{\pi}{2}\)が成立し、かつ\(V = V_0\)では小問(4)より\(E = \sqrt{1 + \dfrac{2 X_d}{X_e}} V_0\)であるため、題意より\(X_e = \dfrac{1}{2} X_d\)とすると、発電機出力は次式のとおり表すことができる。
\(P = \dfrac{\sqrt{1 + \dfrac{2 X_d}{\dfrac{1}{2} X_d}} V_0 \cdot V_0}{X_d + \dfrac{1}{2} X_d} = \dfrac{2 \sqrt{5} }{3} \dfrac{V_0^2}{X_d} \quad \cdots (\text{答}) \)