電験一種 R7年 電力 問2
次の文章は,中距離送電線の四端子定数に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
こう長が50~100kmの中距離送電線は,図のような\(\pi\)形等価回路として模擬することができる。すなわち,送電線路上の直列インピーダンス及び並列アドミタンスを(1)定数として取り扱うことが可能である。
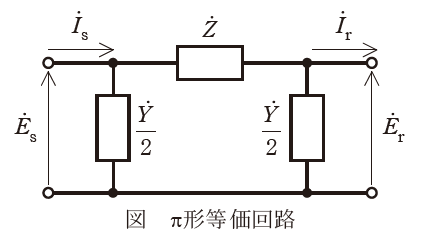
送電端の相電圧\(\dot{E}_{s}\),電流\( \dot{I}_{s}\)と受電端の相電圧\( \dot{E_{r}}\),電流\( \dot{I}_{r}\)の関係は,送電線の四端子定数\(\dot{A}\),\(\dot{B}\),\(\dot{C}\),\(\dot{D}\)を用いて,以下のとおり表すことができる。
\begin{aligned} \begin{bmatrix}\dot{E}_{s}\\ \dot{I}_{s}\end{bmatrix}=\begin{bmatrix}\dot{A}&\dot{B}\\ \dot{C}&\dot{D}\end{bmatrix}\begin{bmatrix}\dot{E}_{r}\\ \dot{I}_{r}\end{bmatrix} \end{aligned}
ここで四端子定数\(\dot{A}\),\(\dot{B}\),\(\dot{C}\),\(\dot{D}\)は,直列インピーダンス\(\dot{Z}\)及び並列アドミタンス\(\dot{Y}\)を用いて以下のとおり表すことができる。
\(\dot{A}=\dot{D}=\)(2)
\(\dot{B}=\)(3)
\(\dot{C}=\)(4)
公称電圧\(275\)kVの三相交流中距離送電線において,\(\dot{Z}=j20~\Omega\),\(\dot{Y}=j0.001~S\),送電端の相電圧\(\dot{E}_{s}=\dfrac{275}{\sqrt{3}}\)kVのとき,受電端を無負荷とした場合の受電端の相電圧\(\dot{E}_{r}\)は(5)kVとなる。
| (イ) | \(1+\displaystyle \frac{\dot{Z}\dot{Y}}{4}\) | (ロ) | \(\dot{Y}\left(1+\displaystyle \frac{\dot{Z}\dot{Y}}{2}\right)\) | (ハ) | \(\dot{Y}\) |
| (ニ) | 分布 | (ホ) | 162 | (ヘ)(1) | 集中 |
| (ト) | \(\dot{Y}(1+\dot{Z}\dot{Y})\) | (チ) | 伝搬 | (リ)(3) | \(\dot{Z}\) |
| (ヌ) | 164 | (ル) | \(1+\dot{Z}\dot{Y}\) | (ヲ)(5) | 160 |
| (ワ)(4) | \(\dot{Y}\left(1+\displaystyle \frac{\dot{Z}\dot{Y}}{4}\right)\) | (カ) | 1 | (ヨ)(2) | \(1+\displaystyle \frac{\dot{Z}\dot{Y}}{2}\) |
出典:令和7年度第一種電気主任技術者電力科目A問題問2
解説
基本的な問題です。電力・管理の二次試験ではこれを難しくしたような問題が出るので理解は必須です。
\(\pi\)形等価回路の四端子定数は以下のようになります。導出方法を理解し過去問を繰り返すことで本番で時間を要せず解けるようにしたいところです。
\begin{aligned} \begin{bmatrix} \dot{A} & \dot{B} \\ \dot{C} & \dot{D} \end{bmatrix} = \begin{bmatrix} 1 + \dfrac{\dot{Z}\dot{Y}}{2} & \dot{Z} \\ \dot{Y} \left(1 + \dfrac{\dot{Z}\dot{Y}}{4}\right) & 1 + \dfrac{\dot{Z}\dot{Y}}{2} \end{bmatrix} \end{aligned}
送電線路上の直列インピーダンス及び並列アドミタンスをどのように扱えるか
分布定数回路: インピーダンスやアドミタンスが線路全体に均一に分布していると考える回路。長距離送電線に適用。
集中定数回路: 短距離送電線や中距離送電線の等価回路のように、回路要素が特定の点に集中していると考える回路。
問題は集中定数回路にあたります。
四端子定数\(\dot{A}\),\(\dot{B}\),\(\dot{C}\),\(\dot{D}\)
結論としては最初に書いた通りです。以下、導出方法です。
なお、全体の受電端開放時と受電端短絡時で求める方法は一般的でありどこにでも解説があるので、別のやり方でやります。
この方法を使用することは二次試験の問題ではあるので、覚えておいた方が得です。
並列アドミタンス\( \dfrac{\dot{Y}}{2}\)、直列インピーダンス\(\dot{Z}\)、並列アドミタンス\( \dfrac{\dot{Y}}{2}\)それぞれの四端子定数を求め、それらを掛け合わせます。
まず並列アドミタンス\( \dfrac{\dot{Y}}{2}\)単独の四端子定数を求めます。
並列アドミタンスの場合、開放時は並列アドミタンスに全ての電圧がかかりますので\(\dot{E}_{s}= \dot{E}_{r}\)です。
また、短絡時は全ての電流が短絡部分に流れるため、\(\dot{I}_{s}= \dot{I}_{r}\)です。よって\(\dot{A} = \dot{D} = 1\)です。
短絡時、電圧がかかるものがないため\(\dot{B} = 0\)です、
解放時、\(\dot{I}_{s}\)は\( \dot{E}_{r}\)と並列アドミタンス\( \dfrac{\dot{Y}}{2}\)の積で決まるので、\(\dot{C} = \dfrac{\dot{Y}}{2}\)です。
これらを\(\dot{A_Y}\),\(\dot{B_Y}\),\(\dot{C_Y}\),\(\dot{D_Y}\)としてまとめると、
\begin{aligned} \begin{bmatrix} \dot{A_Y} & \dot{B_Y} \\ \dot{C_Y} & \dot{D_Y} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ \dfrac{\dot{Y}}{2} & 1 \end{bmatrix} \end{aligned}
となります。
次に直列インピーダンス\(\dot{Z}\)単独の四端子定数を求めます。
直列インピーダンスの場合でも開放時は\(\dot{E}_{s}= \dot{E}_{r}\)です。
また、短絡時は全ての電流が短絡部分に流れるため、\(\dot{I}_{s}= \dot{I}_{r}\)です。よって\(\dot{A} = \dot{D} = 1\)です。
ここまでは並列アドミタンスと直列インピーダンスで同じです。
短絡時、\(\dot{E}_{s}= \dot{Z} \dot{I}_{s}\)なので\(\dot{B} = \dot{Z}\)です。
また、開放時は電流\( \dot{I}_{s}\)は0ですから、\(\dot{C} = 0\)です。
これらを\(\dot{A_Z}\),\(\dot{B_Z}\),\(\dot{C_Z}\),\(\dot{D_Z}\)としてまとめると、
\begin{aligned} \begin{bmatrix} \dot{A_Z} & \dot{B_Z} \\ \dot{C_Z} & \dot{D_Z} \end{bmatrix} = \begin{bmatrix} 1 & Z \\ 0 & 1 \end{bmatrix} \end{aligned}
となります。
全体の四端子定数はこれらを掛けあわせたものとなります。
\begin{aligned} \begin{bmatrix} \dot{A} & \dot{B} \\ \dot{C} & \dot{D} \end{bmatrix} &= \begin{bmatrix} \dot{A_Y} & \dot{B_Y} \\ \dot{C_Y} & \dot{D_Y} \end{bmatrix} \begin{bmatrix} \dot{A_Z} & \dot{B_Z} \\ \dot{C_Z} & \dot{D_Z} \end{bmatrix} \begin{bmatrix} \dot{A_Y} & \dot{B_Y} \\ \dot{C_Y} & \dot{D_Y} \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 \\ \dfrac{\dot{Y}}{2} & 1 \end{bmatrix} \begin{bmatrix} 1 & Z \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ \dfrac{\dot{Y}}{2} & 1 \end{bmatrix} \\ &= \begin{bmatrix} 1 & \dot{Z} \\ \dfrac{\dot{Y}}{2} & 1 + \dfrac{\dot{Z}\dot{Y}}{2} \end{bmatrix} \begin{bmatrix} 1 & 0 \\ \dfrac{\dot{Y}}{2} & 1 \end{bmatrix} \\ &= \begin{bmatrix} 1 + \dfrac{\dot{Z}\dot{Y}}{2} & \dot{Z} \\ \dot{Y} \left(1 + \dfrac{\dot{Z}\dot{Y}}{4}\right) & 1 + \dfrac{\dot{Z}\dot{Y}}{2} \end{bmatrix} \end{aligned}
\(\pi\)形等価回路の四端子定数が導けました。
よって答えは
(2)ヨ \(1+\displaystyle \frac{\dot{Z}\dot{Y}}{2}\)
(3)リ \(\dot{Z}\)
(4)ワ \(\dot{Y}\left(1+\displaystyle \frac{\dot{Z}\dot{Y}}{4}\right)\)
です。
受電端を無負荷とした場合の受電端の相電圧\(\dot{E}_{r}\)
無負荷であることから受電端の電流\( \dot{I}_{r} = 0\)です。
よって以下が成り立ちます。
\begin{aligned} \dot{E}_{s} &= \dot{A} \dot{E}_{r} \\ \end{aligned}
後は\(\dot{A}\)を用いて\(\dot{E}_{r}\)を求めます。
\begin{aligned} \dot{E}_{r} &= \dfrac{\dot{E}_{s} }{\dot{A}}\\ &= \dfrac{\dot{E}_{s} }{1 + \dfrac{\dot{Z}\dot{Y}}{2}} \\ &= \dfrac{\dfrac{275}{\sqrt{3}}}{1 + \dfrac{(j20)(j0.001)}{2}} \\ &= \frac{275}{0.99\sqrt{3}} \\ &\fallingdotseq 160.39 \\ \end{aligned}
よって答えは(ヲ)の160です。
- (1)ヘ 集中
- (2)ヨ \(1+\displaystyle \frac{\dot{Z}\dot{Y}}{2}\)
- (3)リ \(\dot{Z}\)
- (4)ワ \(\dot{Y}\left(1+\displaystyle \frac{\dot{Z}\dot{Y}}{4}\right)\)
- (5)ヲ 160