電験一種 R7年 理論 問7
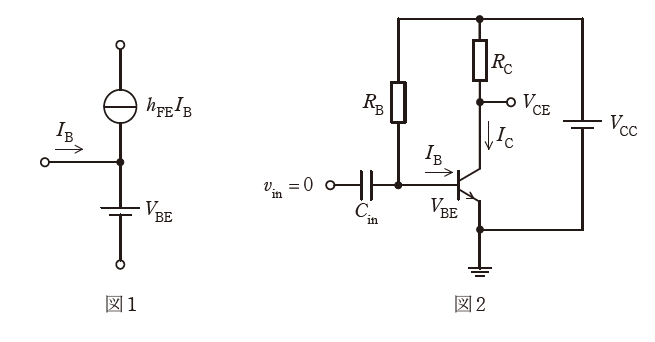
次の文章は,エミッタ接地増幅回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。ただし,npn トランジスタの直流等価回路は図1で表せるとする。図2及び図3に示すエミッタ接地増幅回路はいずれも入力電圧を加えない状態( \(v_{in}=0\) )とし,そのバイアス電流及び電圧について考える。
図2の回路において,トランジスタのベース・エミッタ間電圧 \(V_{BE}\) を用いてベース電流を求め,トランジスタの直流における電流増幅率 \(h_{FE}\) を用いてコレクタ電流を求めると(1)が得られる。このため,図2のコレクタ・エミッタ間電圧 \(V_{CE}\) は(2)となる。
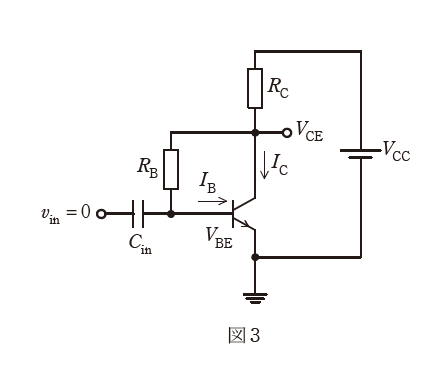
一方,図3のベース電流はコレクタ・エミッタ間電圧 \(V_{CE}\) を用いて(3)と表せる。 \(I_B \ll I_C\) のとき \(R_C\) を流れる電流は \(I_C\) と近似できることを用いて,図3のコレクタ・エミッタ間電圧 \(V_{CE}\) を求めると(4)となる。
以上の結果を用いて,\(V_{CC}=20\) V,\(V_{BE}=0.6\) V,\(R_C=1\) kΩ,\(h_{FE}=200\)であるとき図2及び図3において \(V_{CE}=10\) Vとなるように \(R_B\) を定める。図 2の\(R_B\) は 388 kΩとなり,図3の \(R_B\) は(5)kΩとなる。この状態でそれぞれの回路の \(h_{FE}\) が 200 から 220 に変化したとき,図2の \(V_{CE}\) は9.0Vとなるのに対して,図3の \(V_{CE}\) はおおよそ(6)V となるため,図3の方が \(h_{FE}\) の変動がバイアス電位に与える影響を抑えることができる構成といえる。
| (イ) | 9.24 | (ロ)(6) | 9.54 | (ハ) | 9.84 |
| (ニ) | 88 | (ホ)(5) | 188 | (ヘ) | 288 |
| (ト) | \(\displaystyle \frac{V_{CE}}{R_C}\) | (チ) | \(\displaystyle R_C \frac{h_{FE}(V_{CC}-V_{BE})}{R_B+h_{FE}R_C}\) | (リ) | \(\displaystyle V_{CC}-h_{FE}\dfrac{R_C}{R_B} V_{BE}\) |
| (ヌ)(3) | \(\displaystyle \frac{V_{CE}-V_{BE}}{R_B}\) | (ル) | \(\displaystyle \frac{V_{CC}-V_{BE}}{R_B}\) | (ヲ) | \(\displaystyle \frac{V_{BE}-V_{CE}}{R_B}\) |
| (ワ)(1) | \(\displaystyle h_{FE}\frac{V_{CC}-V_{BE}}{R_B}\) | (カ) | \(\displaystyle h_{FE} \frac{R_C}{R_B}(V_{CC}-V_{BE})\) | (ヨ) | \(\displaystyle h_{FE}\frac{V_{CE}-V_{BE}}{R_B}\) |
| (タ)(4) | \(\displaystyle V_{CC}-R_C\frac{h_{FE}(V_{CC}-V_{BE})}{R_B+h_{FE}R_C}\) | ||||
| (レ)(2) | \(\displaystyle V_{CC}-h_{FE}\frac{R_C}{R_B}(V_{CC}-V_{BE})\) | ||||
| (ソ) | \(\displaystyle V_{CC}-R_C\frac{h_{FE}V_{BE}}{R_B+h_{FE}R_C}\) | ||||
出典:令和7年度第一種電気主任技術者理論科目B問題問7
解説
(4)の式変形が面倒かもしれませんが順を追って考えれば特につまずく点もなく解ける問題かと思います。
トランジスタの直流における電流増幅率 \(h_{FE}\) を用いてコレクタ電流を求める
キルヒホッフの電圧則より、ベース・エミッタ間には\(v_{in}=0\)であり、またコンデンサに直流電流は流れないため以下の式が成り立ちます。
\begin{aligned} V_{CC} = R_B I_B + V_{BE} \end{aligned}
よってベース電流 \(I_B\) は以下のように求められます。
\begin{aligned} I_B = \frac{V_{CC} - V_{BE}}{R_B} \end{aligned}
これに電流増幅率をかけたものがコレクタ電流なので、
\begin{aligned} I_C &= h_{FE} I_B \\ &= h_{FE} \frac{V_{CC} - V_{BE}}{R_B}\\ \end{aligned}
となります。答えは(ワ)の\(\displaystyle h_{FE}\frac{V_{CC}-V_{BE}}{R_B}\)です。
コレクタ・エミッタ間電圧 \(V_{CE}\)
図2の回路の出力側に注目します。コレクタ抵抗\(R_C\)を流れる電流は、問7(1)で求めたコレクタ電流\(I_C\)です。電源電圧 \(V_{CC}\)は、コレクタ抵抗\(R_C\)にかかる電圧と、コレクタ・エミッタ間電圧\(V_{CE}\)の和に等しくなります。
キルヒホッフの電圧則より、以下の式が成り立ちます。
\begin{aligned} V_{CC} &= R_C I_C + V_{CE} \\ &= V_{CC} - R_C I_C \\ \end{aligned}
ここに、(1)で求めた\(I_C\)を代入すると、
\begin{aligned} V_{CE} &= V_{CC} - R_C \left( h_{FE} \frac{V_{CC} - V_{BE}}{R_B} \right) \\ V_{CE} &= V_{CC} - h_{FE} \frac{R_C}{R_B} (V_{CC} - V_{BE}) \\ \end{aligned}
となります。よって答えは(レ)の\(\displaystyle V_{CC}-h_{FE}\frac{R_C}{R_B}(V_{CC}-V_{BE})\)です。
図3のベース電流をコレクタ・エミッタ間電圧 \(V_{CE}\) を用いて表す
図3の回路は、ベース抵抗\(R_B\)がコレクタとベースの間に接続されている「自己バイアス回路」と呼ばれる構成です。
ベース抵抗\(R_B\)にかかる電圧は、コレクタ・エミッタ間電圧\(V_{CE}\)とベース・エミッタ間電圧\(V_{BE}\)の差で表されます。
よってベース電流は以下となります。
\begin{aligned} I_B &= \frac{V_{CE} - V_{BE}}{R_B} \\ \end{aligned}
答えは(ヌ)の\(\displaystyle \frac{V_{CE}-V_{BE}}{R_B}\)です。
図3のコレクタ・エミッタ間電圧 \(V_{CE}\) を求める
問題の条件より、\(R_C\)を流れる電流は\(I_B+I_C\)ですが\(I_C\)と近似できるとあります。
コレクタ電流 \(I_C\) は \(I_C = h_{FE} I_B\) なので、(3)で求めた\(I_B\)の式を代入します。
\begin{aligned} I_C &= h_{FE} \frac{V_{CE} - V_{BE}}{R_B} \\ \end{aligned}
次に、図3の出力側のループにキルヒホッフの電圧則を適用します。
\begin{aligned} V_{CC} &= R_C I_C + V_{CE} \\ &= R_C \left( h_{FE} \frac{V_{CE} - V_{BE}}{R_B} \right) + V_{CE} \\ \end{aligned}
この式を\(V_{CE}\)について整理します。
\begin{aligned} V_{CC} &= \frac{h_{FE} R_C}{R_B} (V_{CE} - V_{BE}) + V_{CE} \\ &= \frac{h_{FE} R_C}{R_B} V_{CE} - \frac{h_{FE} R_C}{R_B} V_{BE} + V_{CE} \\ \end{aligned}
\begin{aligned} V_{CC} + \frac{h_{FE} R_C V_{BE}}{R_B} &= V_{CE} \left( \frac{h_{FE} R_C}{R_B} + 1 \right) \\ V_{CC} + \frac{h_{FE} R_C V_{BE}}{R_B} &= V_{CE} \left( \frac{h_{FE} R_C + R_B}{R_B} \right) \\ \end{aligned}
\begin{aligned} V_{CE} &= \dfrac{V_{CC} + \dfrac{h_{FE} R_C V_{BE}}{R_B}}{\dfrac{h_{FE} R_C + R_B}{R_B}} \\ &= \frac{R_B V_{CC} + h_{FE} R_C V_{BE}}{R_B + h_{FE} R_C} \\ &= \frac{R_B V_{CC} + h_{FE} R_C V_{CC} - h_{FE} R_C V_{CC} + h_{FE} R_C V_{BE}}{R_B + h_{FE} R_C} \\ &= \frac{R_B V_{CC} + h_{FE} R_C V_{CC}}{R_B + h_{FE} R_C} - \frac{ h_{FE} R_C V_{CC} - h_{FE} R_C V_{BE}}{R_B + h_{FE} R_C} \\ &= V_{CC}-R_C\frac{h_{FE}(V_{CC}-V_{BE})}{R_B+h_{FE}R_C} \\ \end{aligned}
よって答えは(タ)の\(\displaystyle V_{CC}-R_C\frac{h_{FE}(V_{CC}-V_{BE})}{R_B+h_{FE}R_C}\)です。
図3の\(R_B\)
問題文にて与えられた数値を用い計算します。
\(V_{CC} = 20~\text{V},~ V_{BE} = 0.6~\text{V},~ R_C = 1~\text{k}\Omega = 1 \times 10^3~\Omega,~ h_{FE} = 200,~ V_{CE} = 10~\text{V} \)
\begin{aligned} 10 &= 20 - (1 \times 10^3) \cdot \frac{200(20 - 0.6)}{R_B + 200 \cdot (1 \times 10^3)} \\ 10 - 20 &= -1000 \cdot \frac{200(19.4)}{R_B + 200000} \\ -10 &= -1000 \cdot \frac{3880}{R_B + 200000} \\ 1 &= 100 \cdot \frac{3880}{R_B + 200000} \\ R_B + 200000 &= 100 \cdot 3880 \\ R_B &= 388000 - 200000 \\ R_B &= 188000 \\ \end{aligned}
単位はキロなので答えは(ホ)の188です。
\(h_{FE}\)が200から220に変化したときの図3の\(V_{CE}\)
(4)の式に\(h_{FE} = 220\)と\(R_B = 188 \times 10^3\)を代入して計算します。
\begin{aligned} V_{CE} &= 20 - (1 \times 10^3) \cdot \frac{220(20 - 0.6)}{(188 \times 10^3) + 220 \cdot (1 \times 10^3)} \\ &= 20 - 1000 \cdot \frac{220 \cdot 19.4}{188000 + 220000} \\ &= 20 - 1000 \cdot \frac{4268}{408000} \\ &= 20 - 10.46... \\ V_{CE} &\fallingdotseq 9.54~\text{V} \\ \end{aligned}
よって答えは(ロ)の9.54です。
- (1)ワ \(\displaystyle h_{FE}\frac{V_{CC}-V_{BE}}{R_B}\)
- (2)レ \(\displaystyle V_{CC}-h_{FE}\frac{R_C}{R_B}(V_{CC}-V_{BE})\)
- (3)ヌ \(\displaystyle \frac{V_{CE}-V_{BE}}{R_B}\)
- (4)タ \(\displaystyle V_{CC}-R_C\frac{h_{FE}(V_{CC}-V_{BE})}{R_B+h_{FE}R_C}\)
- (5)ホ 188
- (6)ロ 9.54