電験一種 R7年 理論 問6
次の文章は,電界効果トランジスタの原理に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
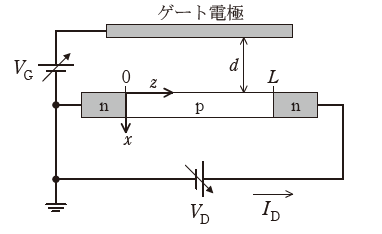
図のように,n形半導体とp形半導体を,左からn-p-nの順に接合させた構造に対して,距離\(d\)を隔てて平行に金属ゲート電極を配置する。n-p-n構造及びゲート電極の,紙面の奥行き方向の長さを\(W\)とする。p形半導体の長さを\(L\)とし,電極及びn形半導体中の抵抗は無視する。また,ゲート電極と半導体間の誘電率を\(\varepsilon\)とする。
図の回路において,\(V_D=0\)とし,\(V_G>0\)を印加した場合を考える。平行平板導体間の静電誘導によって,ゲート電極下面に正の面電荷密度\(+\sigma\)が,半導体側には負の面電荷密度\(-\sigma\)が誘起される。ただし,\(L\gg d\)かつ\(W\gg d\),と仮定し,端部効果は無視する。ゲート電極と半導体の間の電界の\(x\)方向成分を\(E_x\)と定義すると,\(\sigma\)は\(E_x\)と\(\varepsilon\)を用いて次のように表される。
\(\sigma=\)(1) …①
半導体側に誘起される負の電荷は電子の流入によって生じるが,p形半導体には多数の正孔が存在するため,流入した電子は正孔との再結合で消滅する。表面における正孔の面電荷密度を\(\dfrac{\varepsilon}{d}V_{th}\)と仮定すると,p形半導体表面に誘起される電子の面電荷密度の大きさ\(\sigma_e\)は,\(\sigma\)から正孔の面電荷密度を減じた大きさになる。すなわち,
\(\sigma_e=\sigma-\dfrac{\varepsilon}{d}V_{th}\) …②
ただし,\(V_{th}\)は,p形半導体表面の正孔を打ち消すのに必要な\(V_G\)に相当し,しきい値電圧と呼ばれる。
次に,\(V_G>0\),\(V_D>0\)の場合を考える。図に示す\(z\)座標を用いてp形半導体表面の電位を\(V_C(z)\)と定義する。位置\(z\)における\(E_x\)は,\(V_C(z)\),\(V_G\),\(d\)を用いて次のように表される。
\(E_x=\)(2) …③
②式に,①式,③式を代入すると,\(\sigma_e\)は次のように表される。
\(\sigma_e=\dfrac{\varepsilon}{d}\)((3)) …④
p形半導体表面に電子が誘起されている状況では,p形半導体表面がn形に反転していることから,構造全体としてn-n-n接合となり,\(V_D>0\)の印加により,電流が流れる。面電荷密度\(-\sigma_e\)の電子が電界により平均速度\(v\)でドリフト運動する場合の電流\(i_D\)は,奥行き長さ\(W\)を考慮し,+z方向を正として次のように表される。
\(i_D=-\sigma_e Wv\) …⑤
\(v\)は,電子の移動度\(\mu\)と,\(z\)方向の電界\(E_z\)を用いて次のように表される。ただし,\(\mu\)は場所によらず一定とする。
\(v=-\mu E_z\) …⑥
\(E_z\)は\(V_C(z)\)を用いて次のように表される。
\(E_z=-\dfrac{\partial V_C(z)}{\partial z}\) …⑦
⑤式に,④式,⑥式,⑦式を代入し,\(I_D=-i_D\)の関係を用いると,\(I_D\)は次のように表される。
\( I_D=\dfrac{\varepsilon \mu W}{d}\)((4)) \( \dfrac{\partial V_C(z)}{\partial z} \quad \cdots\cdots\cdots ⑧\)
定常状態では,電流の連続性から,\(I_D\)は位置\(z\)によらない定数となる。また,\(V_{th}\)も\(z\)によらない定数であると仮定して,⑧式の両辺を\(z=0\)から\(L\)まで\(z\)で積分すると,左辺の積分の値は(4)となる。右辺の積分も実行して,\(V_C(0)=0\)及び\(V_C(L)=V_D\)を適用すると,\(I_D\)は\(V_D\)の関数として\(I_D=\)(5)のように表される。
| (イ)(4) | \(I_DL\) | (ロ) | \(\displaystyle \frac{d}{V_G-V_C(z)}\) | (ハ)(1) | \(\varepsilon E_x\) | (ニ)(3) | \(V_G-V_{th}-V_C(z)\) |
| (ホ) | \(\displaystyle \frac{I_D}{L}\) | (ヘ) | \(\displaystyle \frac{\varepsilon E_x}{2}\) | (ト) | \(2\varepsilon E_x\) | (チ) | \(V_G+V_{th}-V_C(z)\) |
| (リ)(2) | \(\displaystyle \frac{V_G-V_C(z)}{d}\) | (ヌ) | \(\displaystyle \frac{I_D^2L}{2}\) | (ル) | \(\displaystyle \frac{V_G+V_C(z)}{d}\) | (ヲ) | \(V_G-V_{th}+V_C(z)\) |
| (ワ) | \(\displaystyle \frac{\varepsilon\mu WL}{2d}[2(V_G-V_{th})V_D-V_D^2]\) | (カ)(5) | \(\displaystyle \frac{\varepsilon\mu W}{2d L}[2(V_G-V_{th})V_D-V_D^2]\) | ||||
| (ヨ) | \(\displaystyle \frac{\varepsilon\mu W}{2d L}[2(V_G-V_{th})V_D+V_D^2]\) | ||||||
出典:令和7年度第一種電気主任技術者理論科目B問題問6
解説
この手の問題は一見難しいですが、電験一種ではよく読めば細かい知識がなくとも解けるようにはなっています。ただ、本番では慣れていないとそもそも読んでも何を問われているか分からないと思いますので結局過去問周回は重要です。
\(\sigma \)を\(E_x\)と\(\varepsilon\)を用いて表す
ゲート電極と半導体(p形半導体表面)は平行平板コンデンサとして考えることができます。
ゲート電極と半導体の間の電界の\(x\)方向成分は\(E_x\)ですから、面電荷密度はこれに\(\varepsilon\)をかけたものとなり、
\begin{aligned} \sigma &= \varepsilon E_x \\ \end{aligned}
となりますので、答えは(ハ)の\(\varepsilon E_x\)です。
位置\(z\)における\(E_x\)
(2)のとき、\(p\)型半導体の表面には電位\(V_C(z)\)が存在します。
ゲート電極とp形半導体間の電位差は、ゲート電極の電位\(V_G\)と半導体表面の電位\(V_C(z)\)の差です。
したがって、位置\(z\)における電位差は\(V_G - V_C(z)\)となります。
電界\(E_x\)は、この電位差をゲートと半導体間の距離dで割った値です。よって
\begin{aligned} E_x &= \frac{V_G - V_C(z)}{d} \\ \end{aligned}
となりますので、答えは(リ)の\(\displaystyle \frac{V_G-V_C(z)}{d}\)です。
②式に,①式,③式を代入して\(\sigma_e\)を表す
問題に記載の通り代入して式を整理します。
\begin{aligned} \sigma_e &= \sigma - \frac{\varepsilon}{d}V_{th}\\ &= \varepsilon E_x - \frac{\varepsilon}{d}V_{th}\\ &= \varepsilon \frac{V_G - V_C(z)}{d} - \frac{\varepsilon}{d}V_{th}\\ &= \frac{\varepsilon}{d}(V_G - V_{th} - V_C(z)) \\ \end{aligned}
よって答えは(ニ)の\(V_G-V_{th}-V_C(z)\)です。
\(I_D\)を\(z=0\)から\(x\)まで積分する
難しいことはなく、ただ\(I_D\)を積分するだけです。
\begin{aligned} I_D \int_{0}^{L} \mathrm{d}z &= I_D L \\ \end{aligned}
よって答えは(イ)の\(I_DL\)です。
右辺を積分して\(I_D\)を示す
ここは(4)が\(I_D L\)であることと、(3)が分かっていれば積分をしなくともつじつまが合うのが(カ)だけなので答えが分かります。
以下、右辺を積分します。※ここは数学的に誤りがあれば指摘もらえると助かります。
積分する式は以下です。
\begin{aligned} \int_{0}^{L} \frac{\varepsilon\mu W}{d}(V_G - V_{th} - V_C(z))\frac{\partial V_C(z)}{\partial z} \mathrm{d}z \end{aligned}
\(u=V_C(z)\)とおいて両辺を微分します。\(V_C(z)\)は\(z\)のみの関数なので\(\mathrm{d}\)でも\(\partial \)でも計算結果は同じです。
\begin{aligned} \dfrac{\mathrm{d}u}{\mathrm{d}z} &= \dfrac{\partial V_C(z) }{\partial z} \\ \mathrm{d}u &= \dfrac{\partial V_C(z) }{\partial z} \mathrm{d}z \end{aligned}
元の積分の式を置換します。ここで積分範囲は問題より\(z=0\)のとき\(V_C(0)=0\)、\(z=L\)のとき\(V_C(L)=V_D\)なので、\(0~V_D\)となります。
\begin{aligned} \frac{\varepsilon\mu W}{d} \int_{0}^{V_D} (V_{G}-V_{th}-u)du &= \int_{0}^{V_D} (V_{G}-V_{th}-u)du\\ &= \frac{\varepsilon\mu W}{d} \left[ (V_{G}-V_{th})u - \frac{1}{2}u^2 \right]_{0}^{V_D} \\ &=\frac{\varepsilon\mu W}{d} \left[ (V_{G}-V_{th})V_D - \frac{1}{2}V_D^2 \right] \\ &= \frac{\varepsilon\mu W}{2d }\left[2(V_G-V_{th})V_D-V_D^2\right] \\ \end{aligned}
これは(4)で積分した結果の右辺なので、以下が成り立ちます。
\begin{aligned} I_D L &= \frac{\varepsilon\mu W}{2d }\left[2(V_G-V_{th})V_D-V_D^2\right] \\ I_D &= \frac{\varepsilon\mu W}{2d L}\left[2(V_G-V_{th})V_D-V_D^2\right] \\ \end{aligned}
よって答えは(カ)の\(\displaystyle \frac{\varepsilon\mu W}{2d L}[2(V_G-V_{th})V_D-V_D^2]\)です。
- (1)ハ \(\varepsilon E_x\)
- (2)リ \(\displaystyle \frac{V_G-V_C(z)}{d}\)
- (3)ニ \(V_G-V_{th}-V_C(z)\)
- (4)イ \(I_DL\)
- (5)カ \(\displaystyle \frac{\varepsilon\mu W}{2d L}\left[2(V_G-V_{th})V_D-V_D^2\right]\)