電験一種 R7年 理論 問5
次の文章は,三相交流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
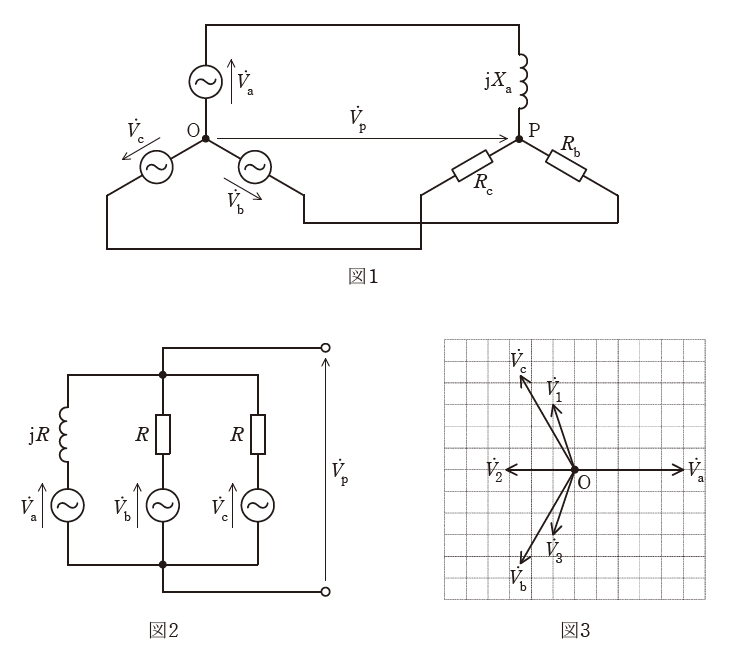
図1の回路は,Y結線の対称三相電源にY結線の不平衡三相負荷が接続された不平衡三相回路である。不平衡負荷は,一つの誘導性負荷及び二つの等しい純抵抗負荷(電灯)から構成されている。ただし,誘導性負荷のリアクタンスは\(X_a\),抵抗負荷の抵抗値は\(R_b\),\(R_c\)であり,\(X_a=R_b=R_c=R\)とする。
ここで,対称三相電源の相回転の順が\(\dot{V_a} \rightarrow \dot{V_b} \rightarrow \dot{V_c}\)であるとき,以下の手順に従って,対称三相電源の相回転の順(相順)と電灯の明暗の関係を考察する。
図1の不平衡三相回路は,図2に示す等価回路に変換できる。ミルマンの定理より,図2の等価回路における中性点\(O\)-\(P\)間の電圧\(\dot{V_p}\)は,
\( \dot{V_p}=\dfrac{\dfrac{\dot{V_a}}{jR}+\dfrac{\dot{V_b}}{R}+\dfrac{\dot{V_c}}{R}}{\dfrac{1}{jR}+\dfrac{1}{R}+\dfrac{1}{R}} = \)(1)\(\cdots \text{①}\)
となる。ここで対称三相電源であることから,\(\dot{V_b}+\dot{V_c}=-\dot{V_a}\)の関係が成り立つので,①式の\(\dot{V_p}\)は,\(\dot{V_a}\)を用いて,
\(\dot{V_p}=\)(2)\(\cdots \text{②}\)
と表すことができる。
図3は,相回転の順が\(\dot{V_a} \rightarrow \dot{V_b} \rightarrow \dot{V_c}\)である対称三相電源のベクトル図を示したものであり,②式の\(\dot{V_p}\)を表すベクトルは図3の(3)である。
ここで,\(X_a=R_b=R_c\)であることに注意すれば,二つの電灯に流れる電流の大きさは\(\left| \dot{V_b}-\dot{V_p} \right|\)と\(\left| \dot{V_c}-\dot{V_p}\right|\)に比例する。また,図3のベクトル図より,\(\left|\dot{V_b}-\dot{V_p}\right|\)と\(\left|\dot{V_c}-\dot{V_p}\right|\)の間には,(4)の関係が成立する。したがって,二つの電灯\(R_b\)と\(R_c\)の明るさの関係は,(5)。
| (イ) | \(\displaystyle \frac{j\dot{V}_a+\dot{V}_b+\dot{V}_c}{2-j}\) | (ロ) | \(|\dot{V}_b-\dot{V}_p| > |\dot{V}_c-\dot{V}_p|\) | (ハ) | \(\dot{V}_2\) |
| (ニ)(4) | \(|\dot{V}_b-\dot{V}_p| < |\dot{V}_c-\dot{V}_p|\) | (ホ)(1) | \(\displaystyle \frac{-j\dot{V}_a+\dot{V}_b+\dot{V}_c}{2-j}\) | (ヘ) | \(\displaystyle \frac{1-j3}{5}\dot{V}_a\) |
| (ト)(3) | \(\dot{V}_3\) | (チ)(2) | \(\displaystyle -\frac{1+j3}{5}\dot{V}_a\) | (リ) | \(|\dot{V}_b-\dot{V}_p|=|\dot{V}_c-\dot{V}_p|\) |
| (ヌ) | \(\displaystyle \frac{1+j3}{5}\dot{V}_a\) | (ル) | \(\displaystyle \frac{-j\dot{V}_a+\dot{V}_b+\dot{V}_c}{2+j}\) | (ヲ) | \(\dot{V}_1\) |
| (ワ) | 電灯\(R_b\)が電灯\(R_c\)よりも明るくなる | ||||
| (カ)(5) | 電灯\(R_b\)が電灯\(R_c\)よりも暗くなる | ||||
| (ヨ) | 電灯\(R_b\)と電灯\(R_c\)は同じ明るさになる | ||||
出典:令和7年度第一種電気主任技術者理論科目B問題問5
解説
基本的に誘導に従えば解ける問題なので難しくはないです。(4)と(5)は過去問にはない問われ方ですが、図を見ればすぐ分かる内容ではあります。(本番中にその発想ができるかは分かりませんが)
図2の等価回路における中性点\(O\)-\(P\)間の電圧\(\dot{V_p}\)
\(\dfrac{1}{j}=-j\)であることを利用すれば簡単です。
\begin{aligned} \dot{V_p} &=\dfrac{\dfrac{\dot{V_a}}{jR}+\dfrac{\dot{V_b}}{R}+\dfrac{\dot{V_c}}{R}}{\dfrac{1}{jR}+\dfrac{1}{R}+\dfrac{1}{R}} \\ &=\dfrac{-j\dot{V_a}+\dot{V_b}+\dot{V_c}}{-j+1+1} \\ &=\dfrac{-j\dot{V}_a+\dot{V}_b+\dot{V}_c}{2-j} \\ \end{aligned}
よって答えは(ホ)の\(\displaystyle \frac{-j\dot{V}_a+\dot{V}_b+\dot{V}_c}{2-j}\)です。
①式の\(\dot{V_p}\)を\(\dot{V_a}\)を用いて表す
(1)の答えに\(\dot{V_b}+\dot{V_c}=-\dot{V_a}\)を代入し、式を整理します。
\begin{aligned} \dot{V_p} &=\dfrac{-j\dot{V}_a+\dot{V}_b+\dot{V}_c}{2-j} \\ &= \frac{-j\dot{V_a} - \dot{V_a}}{2-j} \\ &= \frac{-(1+j)\dot{V_a}}{2-j} \\ &= \frac{-(1+j)\dot{V_a}}{(2-j)} \times \frac{(2+j)}{(2+j)} \\ &= \frac{-(2+j+2j+j^2)\dot{V_a}}{5} \\ &= -\frac{1+3j}{5}\dot{V_a} \\ \end{aligned}
よって答えは(チ)の\(\displaystyle -\frac{1+j3}{5}\dot{V}_a\)です。
②式の\(\dot{V_p}\)を表すベクトル
(2)より、\(\dot{V_p}\)は\(\displaystyle -\frac{1+j3}{5}\dot{V}_a\)なので、\(\dot{V}_a\)を基準に左下のベクトルであることが分かります。
これを示しているのは\(\dot{V}_3\)です。
よって答えは(ト)の\(\dot{V}_3\)です。
\(\left|\dot{V_b}-\dot{V_p}\right|\)と\(\left|\dot{V_c}-\dot{V_p}\right|\)に成立する関係
(3)より\(\dot{V_p} = \dot{V}_3\)なのでそれと\(\dot{V_b}\)と\(\dot{V_c}\)の関係を考えます。
図3より、\(\left|\dot{V_b}-\dot{V}_3\right|\)と\(\left|\dot{V_c}-\dot{V}_3\right|\)では明らかに\(\left|\dot{V_c}-\dot{V}_3\right|\)の方が長いです。
よって答えは(ニ)の\(|\dot{V}_b-\dot{V}_p| < |\dot{V}_c-\dot{V}_p|\)です。
二つの電灯\(R_b\)と\(R_c\)の明るさの関係
ここは当然電流が大きい方が明るくなるため、(4)より\(|\dot{V}_c-\dot{V}_p|\)の方が明るくなるといえます。
よって答えは(カ)の電灯\(R_b\)が電灯\(R_c\)よりも暗くなるです。
- (1)ホ \(\displaystyle \frac{-j\dot{V}_a+\dot{V}_b+\dot{V}_c}{2-j}\)
- (2)チ \(\displaystyle -\frac{1+j3}{5}\dot{V}_a\)
- (3)ト \(\dot{V}_3\)
- (4)ニ \(|\dot{V}_b-\dot{V}_p| < |\dot{V}_c-\dot{V}_p|\)
- (5)カ 電灯\(R_b\)が電灯\(R_c\)よりも暗くなる