電験一種 R7年 理論 問4
次の文章は,回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
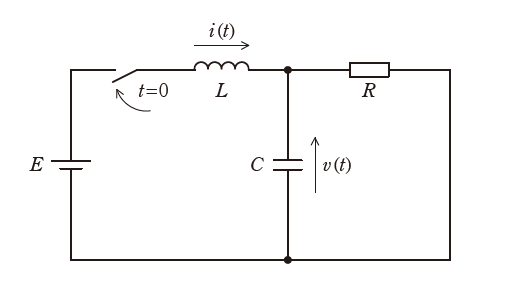
図に示す直流電圧源\(E\),インダクタンス\(L\)のコイル,静電容量\(C\)のコンデンサ,抵抗値\(R\)の抵抗,スイッチからなる回路を考える。時刻\(t \lt 0 \)でスイッチは開いており,コイルの磁束とコンデンサの電荷は零とする。\(t=0\)でスイッチを閉じた。
\(t \geqq 0\)でのコイルの電流を\(i(t)\),コンデンサの電圧を\(v(t)\)とすると,回路図より\(i(t)\)と\(v(t)\)との間には次の関係式が成立する。
\(L\dfrac{\mathrm{d}}{\mathrm{d}t}i(t)=\)(1) …①
\(C\dfrac{\mathrm{d}}{\mathrm{d}t}v(t)=\)(2) …②
回路の初期条件と②式から\(t=0\)では\(\dfrac{\mathrm{d}}{\mathrm{d}t}v(t)\mid_{t=0}=\)(3)である。
②式を微分した式に①式を代入すると\(v(t)\)の二階の微分方程式が得られる。\(v(t)\)の過渡解が減衰振動となるのは,その特性多項式の根が共役複素根となるときであり,条件(4)が成立するときである。
次に,\(t>0\)で\(v(t)\)が満たす不等式を導く。ここでは,詳細な導出は省略するが,①式と②式を利用して回路のエネルギー収支の式
\( \displaystyle \int_{0}^{t}Ei(\tau)\mathrm{d}\tau=\frac{1}{2}L[i(t)]^{2}+\frac{1}{2}C[v(t)]^{2}+\frac{1}{R}\int_{0}^{t}[v(\tau)]^{2}\mathrm{d}\tau \)
を変形してゆくと,以下の式が得られる。
\( \displaystyle C\left\{Ev(t)-\frac{1}{2}[v(t)]^{2}\right\}=\frac{1}{2}C^{2}L\left[\frac{\mathrm{d}}{\mathrm{d}t}v(t)\right]^{2}+\frac{CL}{R}\int_{0}^{t}\left[\frac{\mathrm{d}}{\mathrm{d}\tau}v(\tau)\right]^{2}\mathrm{d}\tau \quad \cdots\cdots\cdots ③ \)
③式の右辺の符号に注意すると,左辺のコンデンサの電圧\(v(t)\)は\(t>0\)で不等式(5)を満たすことが分かる。
| (イ) | \(\displaystyle \frac{1}{R^2}-\frac{4C}{L} \gt 0\) | (ロ) | \(E+v(t)\) | (ハ) | \(i(t)-\displaystyle \frac{2v(t)}{R}\) |
| (ニ)(5) | \(0\lt v(t)\lt 2E\) | (ホ)(3) | \(0\) | (ヘ) | \(\displaystyle \frac{E}{CR}\) |
| (ト)(2) | \(i(t)-\displaystyle \frac{v(t)}{R}\) | (チ) | \(\displaystyle -\frac{E}{CR}\) | (リ)(1) | \(E-v(t)\) |
| (ヌ) | \(\displaystyle 0\lt v(t)\lt \frac{1}{2}E\) | (ル) | \(i(t)+\displaystyle \frac{v(t)}{R}\) | (ヲ) | \(-E\lt v(t)\lt E\) |
| (ワ)(4) | \(\displaystyle \frac{1}{R^2}-\frac{4C}{L}\lt 0\) | (カ) | \(\displaystyle \frac{1}{R^2}-\frac{4C}{L}=0\) | (ヨ) | \(2E-v(t)\) |
出典:令和7年度第一種電気主任技術者理論科目A問題問4
解説
(5)はパッと見て答えが分からなければ時間を要するかもしれません。そのような時は時間を掛けず別の問題に行き余った時間でやるべきでしょう。
回路図により成立する\(L\dfrac{\mathrm{d}}{\mathrm{d}t}i(t)\)
\(L\)と\(C\)でキルヒホッフの電圧則を考えると以下が成立します。
\begin{aligned} E &= L\frac{\mathrm{d}i(t)}{\mathrm{d}t} + v(t) \\ \end{aligned}
これを整理すると
\begin{aligned} L\frac{\mathrm{d}i(t)}{\mathrm{d}t} &= E -v(t)\\ \end{aligned}
となりますので、答えは(リ)の\(E-v(t)\)です。
回路図により成立する\(C\dfrac{\mathrm{d}}{\mathrm{d}t}v(t)\)
\(C\dfrac{\mathrm{d}}{\mathrm{d}t}v(t)\)はコンデンサに流れる電流を示しています。
コンデンサに流れる電流は、\(i(t)\)から抵抗に流れる電流\(\dfrac{v(t)}{R}\)を引いたものに等しいので
\begin{aligned} C\dfrac{\mathrm{d}}{\mathrm{d}t}v(t) &= i(t)-\displaystyle \frac{v(t)}{R}\\ \end{aligned}
となります。答えは(ト)の\(i(t)-\displaystyle \frac{v(t)}{R}\)です。
回路の初期条件
問題に、時刻\(t\lt0\)ではスイッチは開いており、コイルの磁束とコンデンサの電荷は零とあります。
よってコンデンサに流れている電流は\(t=0\)においては0です。
答えは(ホ)の\(0\)です。
過渡解が減衰振動となる条件
式\(C\dfrac{\mathrm{d}}{\mathrm{d}t}v(t)=i(t)-\displaystyle \frac{v(t)}{R}\)を時間\(t\)で微分します。
\begin{aligned} C\frac{d^2v(t)}{dt^2} &= \frac{di(t)}{dt} - \frac{1}{R}\frac{dv(t)}{dt} \\ \end{aligned}
また、式\(L\dfrac{\mathrm{d}i(t)}{\mathrm{d}t} = E - v(t)\)を整理して\(\dfrac{\mathrm{d}i(t)}{\mathrm{d}t}\)の形にします。
\begin{aligned} \dfrac{\mathrm{d}i(t)}{\mathrm{d}t} = \frac{E - v(t)}{L} \\ \end{aligned}
これを代入して\(\dfrac{\mathrm{d}i(t)}{\mathrm{d}t}\)を消去します。
\begin{aligned} C\frac{d^2v(t)}{dt^2} &= \frac{E - v(t)}{L} - \frac{1}{R}\frac{dv(t)}{dt} \\ \end{aligned}
この式を整理して、二階の微分方程式の標準的な形にします。
\begin{aligned} C\frac{d^2v(t)}{dt^2} + \frac{1}{R}\frac{dv(t)}{dt} + \frac{1}{L}v(t) &= \frac{E}{L} \\ \end{aligned}
この微分方程式の解が減衰振動となる条件は、問題の記載の通り特性多項式の根が共役複素数となるときです。
特性多項式は、
\begin{aligned} Cs^2 + \frac{1}{R}s + \frac{1}{L} &= 0 \\ \end{aligned}
です。解の公式により\(s\)を求めます。
\begin{aligned} s &= \dfrac{-\dfrac{1}{R} \pm \sqrt{\left(\dfrac{1}{R}\right)^2 - 4C\left(\dfrac{1}{L}\right)}}{2C} \\ \end{aligned}
ここで、以下の条件の時根号内が負となり、答えが複素数となることが分かります。
\begin{aligned} \frac{1}{R^2} - \frac{4C}{L} < 0 \\ \end{aligned}
よって答えは(ワ)の\(\displaystyle \frac{1}{R^2}-\frac{4C}{L}\lt 0\)です。
コンデンサの電圧\(v(t)\)が満たす不等式
問題で与えられた式は以下です。
\begin{aligned} C\left\{Ev(t)-\frac{1}{2}[v(t)]^{2}\right\}=\frac{1}{2}C^{2}L\left[\frac{\mathrm{d}}{\mathrm{d}t}v(t)\right]^{2}+\frac{CL}{R}\int_{0}^{t}\left[\frac{\mathrm{d}}{\mathrm{d}\tau}v(\tau)\right]^{2}\mathrm{d}\tau \\ \end{aligned}
問題の記載のある「右辺の符号に注意する」とは、右辺は\(\left[\dfrac{\mathrm{d}}{\mathrm{d}t}v(t)\right]^{2}\)、\(\left[\dfrac{\mathrm{d}}{\mathrm{d}\tau}v(\tau)\right]^{2}\)が正の値になるので全体として常に正の値になるということです。
左辺が常に正の値であるためには、\(Ev(t)-\dfrac{1}{2}[v(t)]^{2} \gt 0\)でなければなりません。
この不等式を満たす\(v(t)\)の範囲を考えます。
\begin{aligned} v(t) \gt 0 \text{かつ} E - \frac{1}{2}v(t) \gt 0 \implies v(t) \lt 2E \\ v(t) \lt 0 \text{かつ} E - \frac{1}{2}v(t) \lt 0 \implies v(t) \gt 2E \\ \end{aligned}
上の場合は以下の不等式が成り立ちます。
\begin{aligned} 0 \lt v(t) \lt 2E \\ \end{aligned}
よって答えは(ニ)の\(0\lt v(t)\lt 2E\)です。
なお、下の場合は\(v(t) \lt 0 \)かつ\(v(t) \gt 2E\)を同時に満たせないので解にはなりません。
- (1)リ \(E-v(t)\)
- (2)ト \(i(t)-\displaystyle \frac{v(t)}{R}\)
- (3)ホ \(0\)
- (4)ワ \(\displaystyle \frac{1}{R^2}-\frac{4C}{L}\lt 0\)
- (5)ニ \(0\lt v(t)\lt 2E\)