電験一種 R7年 理論 問3
次の文章は,時分割形乗算器の動作原理に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
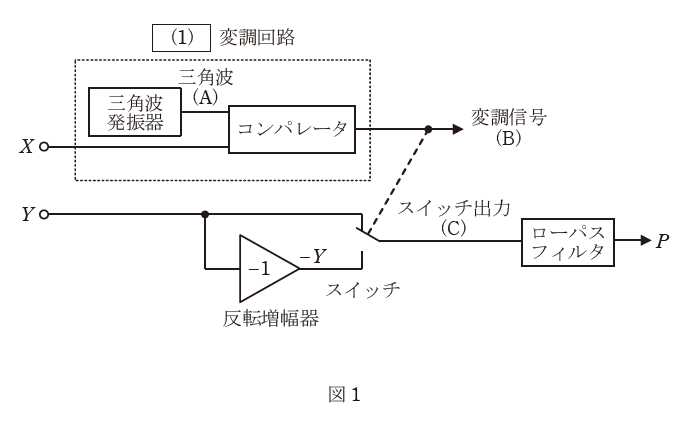
図1に示す回路は,直流電圧の\(X\)及び\(Y\)の積に比例した電圧\(P\)を出力する時分割形乗算器である。また,図2は回路内の各信号波形を表す。
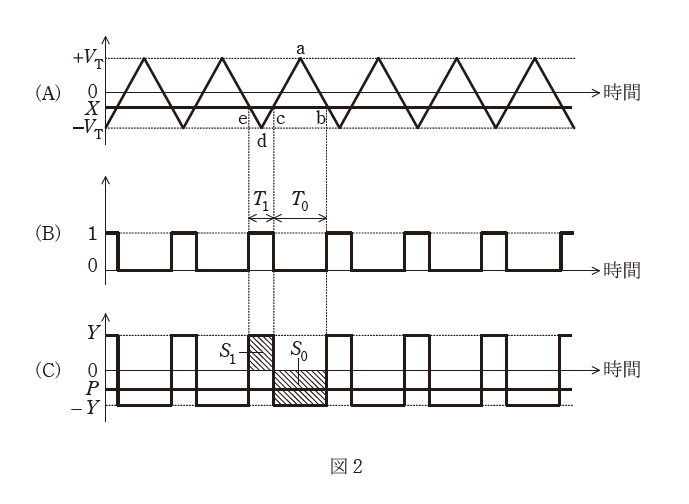
図1の破線枠内の回路は,一般に(1)変調回路と呼ばれる。(1)変調回路では,三角波発振器から図2 (A) に示す振幅が\(\pm V_T\)である三角波を出力し,コンパレータは,\(X\)と三角波の大小関係に応じて,図2(B)に示す論理値0又は1の変調信号を出力する。ただし,\(-V_T \lt X \lt +V_T\)とする。
ここで,図2(A)の\(\triangle abc\)と\(\triangle dec\)が相似であることを利用すれば,\(\dfrac{T_1}{T_0}=\)(2)となる。これを\(X\)について解けば,\(X=\)(3)が得られる。
スイッチは変調信号に応じて接点が切り替わり,その出力波形は図2(C)に示す矩形波で表される。ここで,ローパスフィルタが直流のみを通過させる特性であるなら,\(P\)はスイッチ出力の平均電圧になる。そこで,面積\(S_0\)と面積\(S_1\)に注目すれば,\(Y, T_0\)及び\(T_1\)を用いて,\(P=\)(4)が得られる。
さらに,(3)及び(4)から\(T_0\)及び\(T_1\)を消去すれば,\(P=\)(5)\(XY\)となるから,本回路は積\(XY\)に比例する\(P\)を出力する乗算器であることが分かる。
| (イ) | \((T_1+T_0)(T_1-T_0)V_T\) | (ロ)(5) | \(\displaystyle \frac{1}{V_T}\) | (ハ)(2) | \(\displaystyle \frac{V_T+X}{V_T-X}\) |
| (ニ) | \(\displaystyle \frac{V_T-X}{V_T+X}\) | (ホ) | \((V_T+X)(V_T-X)\) | (ヘ) | 振幅 |
| (ト) | \(V_T\) | (チ) | 周波数 | (リ)(3) | \(\displaystyle \frac{T_1-T_0}{T_1+T_0}V_T\) |
| (ヌ) | \(\displaystyle \frac{T_1+T_0}{T_1-T_0}V_T\) | (ル)(4) | \(\displaystyle \frac{T_1-T_0}{T_1+T_0}Y\) | (ヲ) | \((T_1+T_0)(T_1-T_0)Y\) |
| (ワ) | \(2V_T\) | (カ)(1) | パルス幅 | (ヨ) | \(\displaystyle \frac{T_1+T_0}{T_1-T_0}Y\) |
出典:令和7年度第一種電気主任技術者理論科目A問題問3
解説
難しくはありませんが、この手の問題が苦手な人はそこそこいそうな気がします。
図は何変調回路か
図を見ると、入力Xの大小を三角波と比較して、出力パルスの幅が変化しています。
そのためこれはパルス幅変調回路です。
よって答えは(カ)のパルス幅です。
\(\dfrac{T_1}{T_0}\)を\(\triangle abc\)と\(\triangle dec\)が相似であることを利用して求める
△abcと△decは相似なので、底辺の長さと高さの比は等しいです。よって、三角形の高さの比が分かれば\(\dfrac{T_1}{T_0}\)が分かります。
△abcの高さは\(V_T-X\)です。図を見ると、\(X\)が負の時に\(V_T\)より大きくならないといけないので、\(V_T+X\)ではないことに注意してください。
また、△decの高さは\(V_T+X\)です。
そのため\(\dfrac{T_1}{T_0}\)は
\begin{aligned} \dfrac{T_1}{T_0} &= \dfrac{V_T+X}{V_T-X} \\ \end{aligned}
で表されます。よって答えは(ハ)の\(\displaystyle \frac{V_T+X}{V_T-X}\)です。
(2)を\(X\)について解く
(2)が解けていればその\(X\)を求めるだけです。
\begin{aligned} \frac{T_1}{T_0} &= \frac{V_T + X}{V_T - X}\\ T_1(V_T - X) &= T_0(V_T + X) \\ T_1V_T - T_1X &= T_0V_T + T_0X \\ (T_1 + T_0)X &= (T_1 - T_0)V_T \\ X &= \frac{T_1 - T_0}{T_1 + T_0}V_T \end{aligned}
よって答えは(リ)の\(\displaystyle \frac{T_1-T_0}{T_1+T_0}V_T\)です。
\(Y\)、\(T_0\)、\(T_1\)を用いて\(P\)を表す
平均電圧は波形が作る面積をその時間\(T_1+T_0\)で割ることで求められます。
ここで注意しなければいけないのは、面積\(S_1\)は正、面積\(S_0\)は負として計算することです。(そうしなければ平均電圧は\(Y\)です)
面積\(S_1\)と\(S_0\)はそれぞれ以下で求められます。
\begin{aligned} S_1 &= T_1 Y\\ S_0 &= -T_0 Y\\ \end{aligned}
これの平均を求めればいいので
\begin{aligned} P &= \dfrac{S_1+S_0}{T_1+T_0} \\ &= \dfrac{T_1 Y-T_0 Y}{T_1+T_0} \\ &= \dfrac{T_1 - T_0}{T_1 + T_0}Y \\ \end{aligned}
となり、答えは(ル)の\(\displaystyle \frac{T_1-T_0}{T_1+T_0}Y\)です。
(3)(4)から\(T_0\)、\(T_1\)を消去する
(3)より、
\begin{aligned} \frac{T_1 - T_0}{T_1 + T_0} &= \dfrac{X}{V_T} \end{aligned}
です。これを(4)の答えに代入します。
\begin{aligned} P &= \dfrac{(T_1 - T_0)}{T_1 + T_0}Y \\ &= \dfrac{1}{V_T}XY \\ \end{aligned}
よって答えは(ロ)の\(\displaystyle \frac{1}{V_T}\)です。
- (1)カ パルス幅
- (2)ハ \(\displaystyle \frac{V_T+X}{V_T-X}\)
- (3)リ \(\displaystyle \frac{T_1-T_0}{T_1+T_0}V_T\)
- (4)ル \(\displaystyle \frac{T_1-T_0}{T_1+T_0}Y\)
- (5)ロ \(\displaystyle \frac{1}{V_T}\)