電験一種 R7年 理論 問2
次の文章は,誘導起電力によって正方形コイルに生じる誘導電流に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
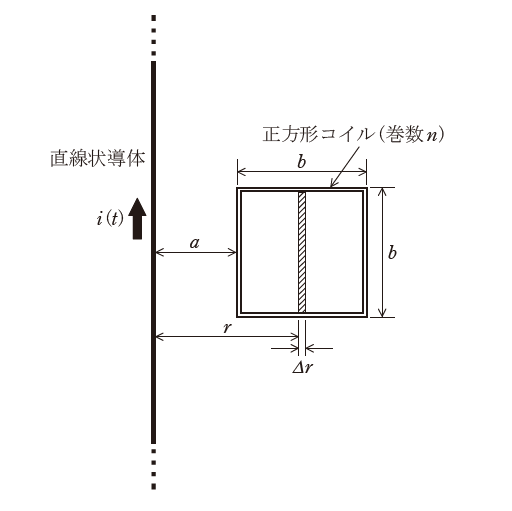
図のように,透磁率\(\mu_0\)の空間の同一平面上に,一辺の長さ\(b\),巻数\(n\)の正方形コイルと無限に長い直線導体とが置かれている。正方形コイルの導体及び直線導体の太さは無視でき,正方形コイルの一辺は直線導体に平行で,距離\(a\)だけ離れている。時刻\(t=0\)において直線導体及び正方形コイルには電流は流れていない。
\(0 \leqq t \leqq t_1\)において,直線導体に流れる電流\(i(t)\)を0から\(I_0\)に一定の割合で増加させた。\(t=t_1\)において,\(i(t)\)によって直線導体から距離\(r\)の位置に生じる磁界の大きさは(1),この位置で長さ\(b\),幅\(\Delta r\)の面(図中のハッチング部)を貫く磁束の大きさは(2)と表される。したがって,\(i(t)\)が正方形コイル内につくる磁束の大きさは,\(0 \leqq t \leqq t_1\)において0から(3)まで増加する。この間,正方形コイルに生じる誘導起電力の大きさは(4)となる。正方形コイルが短絡されている場合,誘導起電力によって誘導電流が流れ,その際に正方形コイルに働く力の向きは(5)である。
| (イ) | \(\displaystyle \frac{n^2\mu_0I_0b}{2\pi t_1}\ln\left(\frac{a+b}{a}\right)\) | (ロ) | \(\displaystyle \frac{n\mu_0I_0b}{2\pi r}\Delta r\) | (ハ) | \(\displaystyle \frac{n\mu_0I_0b}{2\pi}\ln\left(\frac{a+b}{a}\right)\) |
| (ニ)(3) | \(\displaystyle \frac{\mu_0I_0b}{2\pi}\ln\left(\frac{a+b}{a}\right)\) | (ホ)(1) | \(\displaystyle \frac{I_0}{2\pi r}\) | (ヘ) | \(\displaystyle \frac{I_0}{2\pi r^2}\) |
| (ト) | \(\displaystyle \frac{I_0}{\pi r}\) | (チ)(2) | \(\displaystyle \frac{\mu_0I_0b}{2\pi r}\Delta r\) | (リ)(5) | \(\displaystyle \frac{n\mu_0I_0b}{2\pi t_1}\ln\left(\frac{a+b}{a}\right)\) |
| (ヌ) | \(\displaystyle \frac{n\mu_0I_0b}{\pi t_1}\ln\left(\frac{b}{a}\right)\) | (ル) | \(\displaystyle \frac{\mu_0I_0b}{\pi r}\Delta r\) | (ヲ) | \(\displaystyle \frac{\mu_0I_0b}{\pi}\ln\left(\frac{b}{a}\right)\) |
| (ワ) | 直線状導体と引き合う向き | ||||
| (カ)(5) | 直線状導体と反発し合う向き | ||||
| (ヨ) | 直線状導体を中心として回転する向き | ||||
出典:令和7年度第一種電気主任技術者理論科目A問題問2
解説
難しい問題ではないですが後半は悩むところがあるかもしれません。
\(t=t_1\)において,\(i(t)\)によって直線導体から距離\(r\)の位置に生じる磁界の大きさ
電験三種の頃からある基本的な内容であり、電験一種受験者にとってはサービス問題と言っていいでしょう。
答えは(ホ)の\(\displaystyle \frac{I_0}{2\pi r}\)です。
長さ\(b\),幅\(\Delta r\)の面(図中のハッチング部)を貫く磁束の大きさ
網掛け部分の面積は\(b\Delta r\)です。透磁率は\(\mu_0\)なので、そこを貫く磁束の大きさ\(\Delta \Phi\)は
\begin{aligned} \Delta \phi &= \frac{\mu_0I_0b}{2\pi r}\Delta r\\ \end{aligned}
となります。答えは(チ)の\(\displaystyle \frac{\mu_0I_0b}{2\pi r}\Delta r\)です。
\(i(t)\)が正方形コイル内につくる磁束の大きさの増加
正方形の左では\(r=a\)、正方形の右では\(r=a+b\)です。
この時の磁束の大きさ\(\phi\)は、(2)の磁束の大きさを\(a~a+b\)の範囲で積分すればいいので
\begin{aligned} \phi &= \int_{a}^{a+b} d\phi \\ &= \frac{\mu_0 I_0 b}{2\pi } \int_{a}^{a+b} \frac{1}{r} dr \\ &= \frac{\mu_0 I_0 b}{2\pi} \left[ \ln|r| \right]_{a}^{a+b} \\ &= \frac{\mu_0 I_0 b}{2\pi} \left[ \ln(a+b) - \ln(a) \right] \\ &= \frac{\mu_0 I_0 b}{2\pi} \ln\left(\frac{a+b}{a}\right) \\ \end{aligned}
よって答えは(ニ)の\(\displaystyle \frac{\mu_0I_0b}{2\pi}\ln\left(\frac{a+b}{a}\right)\)です。
正方形コイルに生じる誘導起電力の大きさ
コイルに生じる誘導起電力の大きさ\(V\)は\(V= - n\dfrac{\mathrm{d} \phi}{\mathrm{d}t} \)です。(ただし今回は大きさが問われているので符号は関係なし)
ここで、問題より電流\(i(t)\)は\(t_1\)時に\(I_0\)まで単調増加するとありますので、以下で表されます。
\begin{aligned} i(t) &= \dfrac{t}{t_1} I_0 \\ \end{aligned}
これを磁束の式に代入します。
\begin{aligned} \phi(t) &= \frac{\mu_0 I_0b t}{2\pi t_1} \ln\left(\frac{a+b}{a}\right) \\ \end{aligned}
誘導起電力を求めます。
\begin{aligned} V &= - n\dfrac{\mathrm{d}\phi(t)}{\mathrm{d}t} \\ &= -\frac{n\mu_0 I_0 b}{2\pi t_1} \ln\left(\frac{a+b}{a}\right) \\ \end{aligned}
問われているのは大きさなので、答えは(リ)の\(\displaystyle \frac{n\mu_0I_0b}{2\pi t_1}\ln\left(\frac{a+b}{a}\right)\)です。
正方形コイルに働く力の向き
レンツの法則より、正方形コイルには磁束の増加を妨げるような誘導電流が発生します。
直線状導体による磁束は正方形コイルを紙面表から奥へと貫く方向ですから、これを妨げる正方形コイルの電流は反時計回りです。
これによる力は正方形の左では逆向きの電流なので反発し合う向き、右では同じ向きなので引き合う力となりますが、左側の方が近く力が大きいため反発する方が支配的となります。
よって答えは(カ)の直線状導体と反発し合う向きです。
- (1)ホ \(\displaystyle \frac{I_0}{2\pi r}\)
- (2)チ \(\displaystyle \frac{\mu_0I_0b}{2\pi r}\Delta r\)
- (3)ニ \(\displaystyle \frac{\mu_0I_0b}{2\pi}\ln\left(\frac{a+b}{a}\right)\)
- (4)リ \(\displaystyle \frac{n\mu_0I_0b}{2\pi t_1}\ln\left(\frac{a+b}{a}\right)\)
- (5)カ 直線状導体と反発し合う向き