電験一種 R7年 理論 問1
次の文章は,直線電荷が作り出す電界に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
真空中に線電荷密度\(+\lambda(\lambda>0)\)の無限長直線電荷1本が距離\(r\)離れた点に作る電界の大きさ\(E(r)\)は(1)と求められる。ただし,真空中の誘電率を\(\varepsilon_0\)とする。
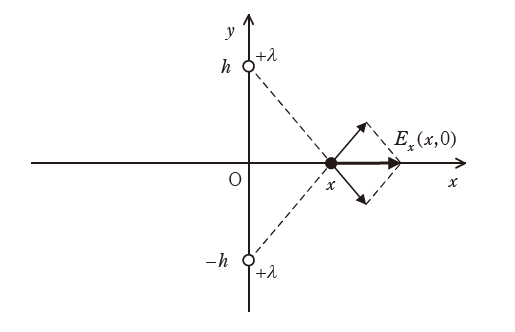
次に,真空中の\(xyz\)座標空間上に線電荷密度\(+\lambda\)の無限長直線電荷2本を置く。それらはともに\(z\)軸に平行で,\(x=0, y=\pm h\)の位置にある。図は\(xy\)平面上での断面を表し,以降は\(xy\)平面で考える。
ここで,\(x\)軸上の電界を考える。図のように二つの線電荷が\(x\)軸上に作る電界の\(x\)成分\(E_x(x,0)\)は(2)となる。\(E_x(x,0)\)が最大となるのは\(x=\)(3)のときで,その最大値は(4)である。原点\(O\)を電位の基準とするとき,点\((x_0,0)\)における電位\(V(x_0,0)\)は(5)である。
| (イ) | \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0}\ln\frac{x_0h}{x_0^2+h^2}\) | (ロ) | \(\displaystyle \frac{\lambda}{4\pi\varepsilon_0r^2}\) | (ハ) | \(\displaystyle \frac{\lambda}{\pi\varepsilon_0}\frac{hx}{(x^2+h^2)^{\frac{3}{2}}}\) |
| (ニ)(2) | \(\displaystyle \frac{\lambda}{\pi\varepsilon_0}\frac{x}{x^2+h^2}\) | (ホ)(1) | \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0r}\) | (ヘ) | \(\displaystyle \frac{h}{\sqrt{3}}\) |
| (ト) | \(\displaystyle \frac{\lambda}{6\pi\varepsilon_0h}\) | (チ)(5) | \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0}\ln\frac{h^2}{x_0^2+h^2}\) | (リ) | \(\displaystyle \frac{\lambda}{\pi\varepsilon_0}\frac{h}{x^2+h^2}\) |
| (ヌ)(4) | \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0h}\) | (ル)(3) | \(h\) | (ヲ) | \(\displaystyle \frac{\lambda}{3\pi\varepsilon_0r^2}\) |
| (ワ) | \(\displaystyle \sqrt{3}h\) | (カ) | \(\displaystyle \frac{3\lambda}{2\pi\varepsilon_0h}\) | (ヨ) | \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0}\ln\frac{x_0^2}{x_0^2+h^2}\) |
出典:令和7年度第一種電気主任技術者理論科目A問題問1
解説
(5)が若干難しいですが基本的には解きやすい問題といえると思います。
無限長直線電荷1本が距離\(r\)離れた点に作る電界の大きさ\(E(r)\)
電験三種の頃からある基本的な内容です。
ガウスの法則より
\begin{aligned} \oint_S \boldsymbol{E} \cdot d\boldsymbol{S} &= \frac{Q}{\varepsilon_0} \\ \end{aligned}
ここで、1mの円筒を考えたとき、円筒の側面積は\(2\pi r\cdot 1\)、電荷は\(\lambda \cdot 1\)です。軸方向は打ち消し合うので、側面だけ考えればよく
\begin{aligned} 2\pi r E &= \frac{\lambda}{\varepsilon_0} \\ E &= \frac{\lambda}{2 \pi \varepsilon_0 r} \end{aligned}
となりますので、答えは(ホ)の\(\displaystyle \frac{\lambda}{2\pi\varepsilon_0r}\)です。
二つの線電荷が\(x\)軸上に作る電界の\(x\)成分\(E_x(x,0)\)
\(+h\)の線電荷と\(x\)の距離は\(\sqrt{x^2+h^2}\)です。\(x\)軸方向の電界\(E_{hx1}\)はこれに\(\dfrac{x}{\sqrt{x^2+h^2}}\)をかけたものになりますので、
\begin{aligned} E_{hx1} &= \frac{\lambda}{2 \pi \varepsilon_0 \sqrt{x^2+h^2}} \cdot \dfrac{x}{\sqrt{x^2+h^2}}\\ &= \frac{\lambda}{2 \pi \varepsilon_0} \cdot \dfrac{x}{x^2+h^2}\\ \end{aligned}
となります。\(-h\)の線電荷による電界の向きも、\(y\)軸方向は逆ですが、\(x\)軸方向の電界\(E_{hx2}\)は同じなので、\(E_{x}\)はこれらを足し合わせればよく、
\begin{aligned} E_{x} &= E_{hx1} + E_{hx2}\\ &= \frac{\lambda}{2 \pi \varepsilon_0} \cdot \dfrac{x}{x^2+h^2} + \frac{\lambda}{2 \pi \varepsilon_0} \cdot \dfrac{x}{x^2+h^2}\\ &= \frac{\lambda}{\pi\varepsilon_0}\frac{x}{x^2+h^2} \\ \end{aligned}
となりますので、答えは(ニ)の\(\displaystyle \frac{\lambda}{\pi\varepsilon_0}\frac{x}{x^2+h^2}\)です。
\(E_x(x,0)\)が最大となる\(x\)
\(\displaystyle \frac{\lambda}{\pi\varepsilon_0}\)は関係ないので\(\dfrac{x}{x^2+h^2}\)が最大になる条件を調べます。
分母と分子を\(x\)で除して分子から\(x\)を消去します。
\begin{aligned} \frac{1}{x+\dfrac{h^2}{x}} \\ \end{aligned}
分母を\(x\)で微分して傾きが\(0\)になる\(x\)を求めます。
\begin{aligned} 0 &= 1-\dfrac{h^2}{x^2} \\ x^2 &= h^2 \\ x &= h \\ \end{aligned}
\(1-\dfrac{h^2}{x^2}\)をもう1回\(x\)で微分すると正の値になりますから、これは極小値であり、これは分母なので、この時電界は最大になります。
よって答えは(ル)の\(h\)です。
\(E_x(x,0)\)の最大値
(2)の答えに(3)の\(x=h\)を代入するだけです。
\begin{aligned} \frac{\lambda}{\pi\varepsilon_0}\frac{x}{x^2+h^2} &= \frac{\lambda}{\pi\varepsilon_0}\frac{h}{h^2+h^2}\\ &= \frac{\lambda}{2\pi\varepsilon_0h} \\ \end{aligned}
よって答えは(ヌ)の\(\displaystyle \frac{\lambda}{2\pi\varepsilon_0h}\)です。
原点\(O\)を電位の基準とするとき,点\((x_0,0)\)における電位\(V(x_0,0)\)
\(y\)軸方向の電界は常に打ち消し合いますので、(2)の\(x\)軸方向の電界を積分すればいいです。
\begin{aligned} V &= - \frac{\lambda}{\pi\varepsilon_0} \int_{0}^{x_0} \frac{x}{x^2+h^2} dx \end{aligned}
置換積分をします。
\( u = x^2 + h^2 \) と置きます。このとき、微分は \( du = 2x \, dx \) となります。したがって、\( x \, dx = \dfrac{1}{2} du \) です。
積分範囲を \(x\) から \(u\) に変更します。
\( x = 0 \) のとき、\( u = 0^2 + h^2 = h^2 \)
\( x = x_0 \) のとき、\( u = x_0^2 + h^2 \)
置換した変数と新しい積分範囲を用いて計算します。
\begin{aligned} V &= - \frac{\lambda}{\pi\varepsilon_0} \int_{h^2}^{x_0^2+h^2} \frac{1}{u} \cdot \frac{1}{2} du \\ &= - \frac{\lambda}{2\pi\varepsilon_0} \int_{h^2}^{x_0^2+h^2} \frac{1}{u} du \\ &= - \frac{\lambda}{2\pi\varepsilon_0} \left[ \ln|u| \right]_{h^2}^{x_0^2+h^2} \\ &= - \frac{\lambda}{2\pi\varepsilon_0} \left[ \ln(x_0^2+h^2) - \ln(h^2) \right] \\ \end{aligned}
対数の性質 \(\ln(a) - \ln(b) = \ln(\dfrac{a}{b})\) を用いて整理します。
\begin{aligned} V &= \frac{\lambda}{2\pi\varepsilon_0} \left[ \ln(h^2) - \ln(x_0^2+h^2) \right] \\ &= \frac{\lambda}{2\pi\varepsilon_0} \ln \frac{h^2}{x_0^2+h^2} \\ \end{aligned}
よって答えは(チ)の\(\displaystyle \frac{\lambda}{2\pi\varepsilon_0}\ln\frac{h^2}{x_0^2+h^2}\)です。
なお、無限遠を基準にして積分するとlogが発散しますので計算はできません。
- (1)ホ \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0r}\)
- (2)ニ \(\displaystyle \frac{\lambda}{\pi\varepsilon_0}\frac{x}{x^2+h^2}\)
- (3)ル \(h\)
- (4)ヌ \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0h}\)
- (5)チ \(\displaystyle \frac{\lambda}{2\pi\varepsilon_0}\ln\frac{h^2}{x_0^2+h^2}\)