電験一種 R6年 理論 問6
次の文章は、円電流が作る磁界中を通過する電子の運動に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。なお、電子の質量を \(m\), 電荷量を \(-e\) (\(e>0\)) とし、電子の質量の変化は無視する。
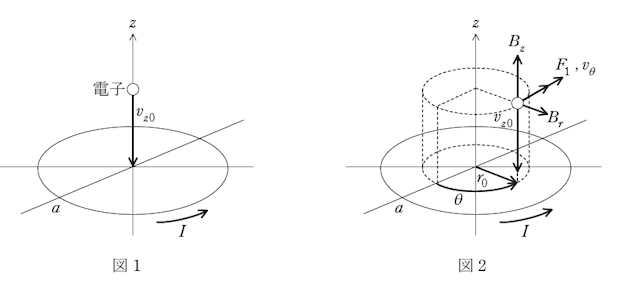
図1のように、原点を中心とする半径 \(a\) の円があり、その円周上に、図に示す方向に一定の電流 \(I\) (\(>0\)) が流れている。円筒座標系の点 \((r, \theta, z)\) における、円電流 \(I\) が作る磁束密度ベクトル \(B\) を、\(B = (B_r, B_\theta, B_z)\) のように表す。
一つの電子が \(z\) 軸上を、\(z\) 軸の正の領域から速度 \(v_{z0}\) (\(<0\)) で \(z\) 軸の負の方向に運動している状況を考える。円電流 \(I\) が作る磁束密度は、\(z\) 軸上では対称性から、\(z\) 軸方向の成分 \(B_z\) 以外は 0 であり、電子が磁界から受けるローレンツ力の大きさは (1) である。
次に、図2のように、電子が \(z\) 軸と平行で距離 \(r_0\) (\(0 < r_0 \ll a\)) だけ離れた軸上を運動する場合を考える。電子の速度の \(z\) 方向成分を \(v_{z0}\) (\(<0\)), その他の方向の速度成分は 0 とする。\(r_0 \neq 0\) の場合には、\(B_r\) は 0 ではなく、電子の速さ \(|v_{z0}|\) が極めて高速であれば、電子はごく短い時間 \(\Delta t\) でのみ磁界から力を受けると近似できる。\(B_r\) によって電子が受けるローレンツ力 \(F_1\) は、図2に示すような半径 \(r_0\) の円の接線に沿って \(\theta\) が増加する方向 (\(\theta+\)方向と定義する) を正にとると、符号も含めて \(F_1 = \)(2) と表される。その結果、\(\theta+\)方向に速度 \(v_\theta\) (\(>0\)) が生じる。ニュートンの第2法則より、\(v_\theta\) の運動方程式は近似的に次のように表される。ただし、\(v_\theta\) の大きさは十分小さく、\(|v_{z0}| \gg |v_\theta|\) とする。
\(\displaystyle m \frac{dv_\theta}{dt} = F_1\)・・・・・・・・・・・・・・①
\(F_1\) が \(z>0\) の限られた微小区間 \(\Delta z\) でのみ作用すると近似すると、力が作用する微小時間 \(\displaystyle \Delta t \left( =\frac{\Delta z}{|v_{z0}|} \right)\) を用いて、\(v_\theta\) は ① 式より、\(\displaystyle v_\theta = \frac{F_1}{m} \Delta t\) と表される。
さらに、\(v_\theta\) と \(B_z\) により、電子はローレンツ力 \(F_2\) を受ける。動径方向に沿って \(r\) が大きくなる方向を正に取り、符号を含めて \(F_2\) を式で表すと、\(F_2 = \)(3) と表される。本問の状況では、\(F_2\) の符号は負であることから、結果的に電子は \(z\) 軸に近づく方向に力を受ける。
ニュートンの第2法則より、速度の \(r\) 方向成分 \(v_r\) の運動方程式は近似的に次のように表される。ただし、\(v_r\) の大きさは十分小さく、\(|v_{z0}| \gg |v_r|\) とする。
\(\displaystyle m \frac{dv_r}{dt} = F_2\) ・・・・・・・・・・・・・・・・②
\(F_2\) も \(F_1\) と同様に、力が作用する微小時間 \(\displaystyle \Delta t \left( =\frac{\Delta z}{|v_{z0}|} \right)\) を用いて、②式より、\(v_r = \)(4)\( \cdot \Delta t\) と表される。力の作用後は動径方向に一定の速さ \(|v_r|\) で \(z\) 軸に近づいていくので、電子が \(z\) 軸に交わるのは時間 \(\displaystyle \frac{r_0}{|v_r|}\) 後である。したがって、力の作用後から \(z\) 軸に交わるまでに電子が \(z\) 軸に沿って進む距離 \(f\) は、\(\displaystyle f = |v_{z0}| \times \frac{r_0}{|v_r|}\) と表される。\(r_0\) が微小である場合には、\(k\) を比例定数として、\(B_r = kr_0 B_z\) と表されることなどを用いると、\(f = \)(5) となり、\(r_0\) に依存しない式で表される。これは、円電流による磁界が電子線の集束レンズとして機能することを意味し、\(f\) は焦点距離に相当する。
| (イ) | \(-e{v_\theta}^2 B_z\) | (ロ)(2) | \(-ev_{z0}B_r\) | (ハ) | \(-ev_{z0}B_\theta\) | (ニ) | \(-ev_\theta {B_z}^2\) |
| (ホ) | \(\displaystyle \frac{m{v_{z0}}^2}{ek{\Delta z}^2 {B_z}^2}\) | (ヘ) | \(\displaystyle -\frac{v_{z0}B_z}{e}\) | (ト)(4) | \(\displaystyle \frac{F_2}{m}\) | (チ) | \(-ev_{z0}{B_z}^2\) |
| (リ)(3) | \(-ev_\theta B_z\) | (ヌ) | \(\displaystyle \frac{F_1}{m}\) | (ル) | \(-ev_{z0}B_z\) | (ヲ) | \(\displaystyle \frac{m^2v_{z0}}{e^2k\Delta z{B_z}^2}\) |
| (ワ) | \(\displaystyle \frac{eF_2}{m}\) | (カ)(5) | \(\displaystyle \frac{m^2{v_{z0}}^2}{e^2k{\Delta z}^2{B_z}^2}\) | (ヨ)(1) | 0 |
出典:令和6年度第一種電気主任技術者理論科目B問題問6
解説
長文のため時間がない理論では厳しい問題かもしれませんが、冷静に考えれば解ける問題ではあります。(4)までは難しいことは書いてはいません。
電子が\(z\)軸上を運動する場合に磁界から受けるローレンツ力
ローレンツ力は以下で表されます。
\(\displaystyle \mathbf{F} = q(\mathbf{v} \times \mathbf{B})\)
問題文にあるように対称性から磁束密度の\(B_z\)以外の成分は0です。
また、同じく問題文より電子の速度ベクトルも\(z\)軸以外の成分は0です。
直交する成分がないので電子が磁界から受けるローレンツ力は0となります。
電子が\(z\)軸上から離れて運動する場合に磁界から受けるローレンツ力
問題文にあるように対称ではないため磁束密度\(B_r\)がこの場合は存在します。
\(B_r\)と\(v_{z0}\)は直交していますので、
\(F_1 = -ev_{z0}B_r\)
の力を受けることとなります。なお、解答群に\(B_r\)を含む選択肢が(ロ)しかないため、\(B_r\)によって受ける力なのだから\(B_r\)が入っていないとおかしいだろうという考えでも正解を選ぶことができます。
\(v_\theta\)と\(B_z\)によって受けるローレンツ力
(2)と同様に考えると以下のようになります。
\(F_2 = -ev_{\theta}B_z\)
\(v_r\)の式
問題文にあるように、\(F_2\)も\(F_1\)と同様に考えることができるので
\(\displaystyle v_r = \frac{F_2}{m} \cdot \Delta t\)
と表せます。
力の作用後から\(z\)軸に交わるまでに電子が\(z\)軸に沿って進む距離\(f\)
問題文と今までの解答により以下の式が成立することが分かっています。
\begin{aligned} F_1 &= -ev_{z0}B_r \\ F_2 &= -ev_\theta B_z \\ v_\theta &= \frac{F_1}{m}\Delta t \\ v_r &= \frac{F_2}{m}\Delta t \\ B_r &= kr_0B_z \\ \Delta t &= \frac{\Delta z}{|v_{z0}|} \\ f &= |v_{z0}| \times \frac{r_0}{|v_r|} \\ \end{aligned}
順に変形していきます。まずは\(F_1\)と\(F_2\)を消去します。
\begin{aligned} v_\theta &= \frac{F_1}{m}\Delta t \\ &= \frac{-ev_{z0}B_r}{m}\Delta t \\ v_r &= \frac{F_2}{m}\Delta t \\ &= \frac{-ev_\theta B_z}{m}\Delta t\\ \end{aligned}
\(v_\theta\)を消去します。
\begin{aligned} v_r &= \frac{-ev_\theta B_z}{m}\Delta t \\ &= \frac{-e \left( \frac{-ev_{z0}B_r}{m}\Delta t \right) B_z}{m}\Delta t \\ &= \frac{e^2v_{z0}B_rB_z}{m^2}\Delta t^2\\ \end{aligned}
\(B_r\)を消去します。
\begin{aligned} v_r &= \frac{e^2v_{z0}B_rB_z}{m^2}\Delta t^2 \\ &= \frac{e^2kv_{z0}r_0{B_z}^2}{m^2}\Delta t^2\\ \end{aligned}
\(\Delta t\)を消去します。
\begin{aligned} v_r &= \frac{e^2kv_{z0}r_0{B_z}^2}{m^2}\Delta t^2 \\ &= \frac{e^2kv_{z0}r_0{B_z}^2}{m^2}\left(\frac{\Delta z}{|v_{z0}|}\right)^2 \\ &= \frac{e^2kr_0B_z^2\Delta z^2}{m^2|v_{z0}|}\\ \end{aligned}
\(f\)から\(v_r\)を消去します。
\begin{aligned} f &= |v_{z0}| \times \frac{r_0}{|v_r|} \\ &= |v_{z0}| \times \frac{r_0}{\left|\frac{e^2kr_0{B_z}^2\Delta z^2}{m^2|v_{z0}|}\right|} \\ &= |v_{z0}| \times \frac{r_0}{\frac{e^2kr_0{B_z}^2\Delta z^2}{m^2|v_{z0}|}} \\ &= |v_{z0}| \times \frac{r_0 \cdot m^2|v_{z0}|}{e^2kr_0{B_z}^2\Delta z^2} \\ &= \frac{{m^2}{v_{z0}}^2}{e^2k\Delta z^2{B_z}^2} \end{aligned}
- (1)ヨ 0
- (2)ロ \(-ev_{z0}B_r\)
- (3)リ \(-ev_\theta B_z\)
- (4)ト \(\displaystyle \frac{F_2}{m}\)
- (5)カ \(\displaystyle \frac{m^2{v_{z0}}^2}{e^2k\Delta z^2{B_z}^2}\)