電験一種 R6年 理論 問5
次の文章は,図の三相交流回路に関する記述である。負荷や再生可能エネルギー電源などに設置された電力変換器から高調波電流が発生すると電圧ひずみが発生する。二次系統など中性点の接地された回路でこの電圧ひずみを計算したい。基本波の角周波数をとして,文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
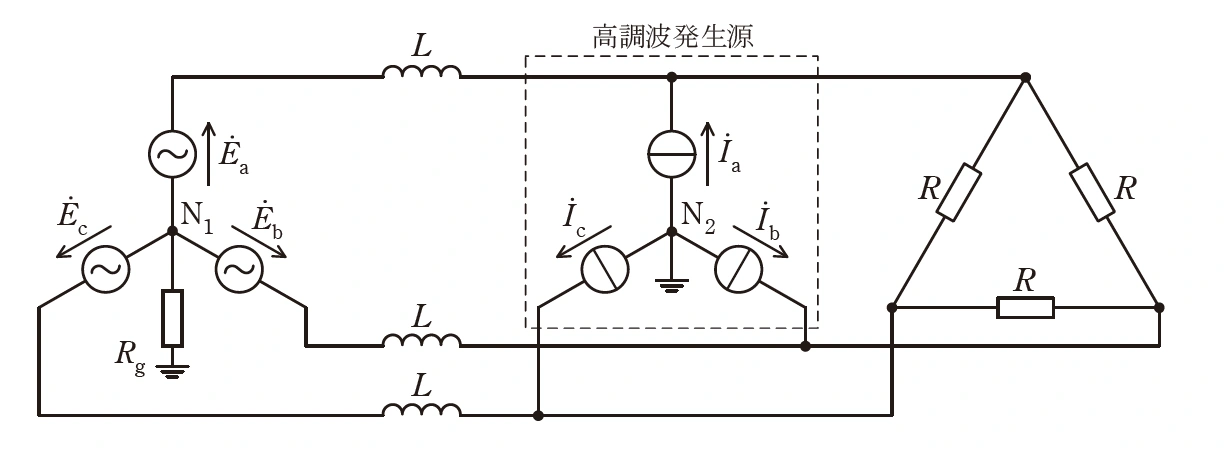
図のように,対称三相交流電圧源 \(\dot{E}_a\), \(\dot{E}_b\), \(\dot{E}_c\) (相順 abc) が,抵抗\( R \)から構成される (1) 結線された負荷と三相電流源に長距離電線により接続されている。長距離電線はインダクタンス\( L \)で表せるとする。電流源の電流は瞬時値形式で以下のように書け,高調波の発生源であることを表している (\(\omega T = 2\pi\))。
\( \begin{cases} i_a(t) = \sqrt{2} I_3 \sin 3\omega t + \sqrt{2} I_5 \sin 5\omega t \\ \displaystyle i_b(t) = \sqrt{2} I_3 \sin 3\omega \left(t - \frac{T}{3}\right) + \sqrt{2} I_5 \sin 5\omega \left(t - \frac{T}{3}\right) = \sqrt{2} I_3 \sin 3\omega t + \sqrt{2} I_5 \sin \left(5\omega t + \frac{2}{3}\pi\right) \\ \displaystyle i_c(t) = \sqrt{2} I_3 \sin 3\omega \left(t + \frac{T}{3}\right) + \sqrt{2} I_5 \sin 5\omega \left(t + \frac{T}{3}\right) = \sqrt{2} I_3 \sin 3\omega t + \sqrt{2} I_5 \sin \left(5\omega t - \frac{2}{3}\pi\right) \end{cases} \)
図の回路は全て線形な要素から構成されており,重ね合わせの理が成り立つ。よって,(2) が全て開放され電圧源のみがある回路 A と,電圧源が全て (3) され電流源のみがある回路 B の状態を独立に計算した後で重ね合わせれば回路の状態を知ることができる。回路 A には高調波は含まれないので,以下回路 B のみを考える。
回路 B の計算では 3 次と 5 次の高調波が生じるが,次数によってインピーダンス等も異なるので次数ごとに取り扱う。5 次の高調波電流三相分の和は (4) であり (5) には流れないため電圧源と負荷にインピーダンスに従って分流する。よって電圧源側へ戻る 5 次電流成分の大きさ(実効値)は (6) であり,これにより生じる高調波発生源の対地電圧の 5 次成分の大きさ(実効値)は (7) である。
一方,3 次の高調波電流は中性点 \(N_2\) の接地線に流れるが,(1) 結線である負荷側には流れない。電圧源側へ戻る 3 次電流成分の大きさ(実効値)は (8), 電圧源の中性点から接地抵抗 \(R_g\) を経て大地へ流れる 3 次電流成分の大きさ(実効値)は (9) であるから高調波発生源の対地電圧の 3 次成分の大きさ(実効値)は (10) である。
| (イ) | 負荷 | (ロ) | インダクタンス \(L\) | (ハ)(5) | 中性点 \(N_2\) の接地線 |
| (ニ)(3) | 短絡 | (ホ)(1) | \(\Delta\) | (ヘ) | Y |
| (ト)(2) | 電流源 | (チ)(9) | \(3I_3\) | (リ)(8) | \(I_3\) |
| (ヌ) | 遮断 | (ル) | 一相分の三倍 | (ヲ)(4) | 0 |
| (ワ)(10) | \(\displaystyle 3I_3\sqrt{R_g^2 + \omega^2 L^2}\) | (カ) | \(\displaystyle \frac{225\omega^2 L^2 I_5}{\sqrt{R^2 + 225\omega^2 L^2}}\) | (ヨ)(7) | \(\displaystyle \frac{5\omega LRI_5}{\sqrt{R^2 + 225\omega^2 L^2}}\) |
| (タ) | \(\displaystyle \frac{27\omega LI_3}{\sqrt{R^2 + 81\omega^2 L^2}}\) | (レ) | \(\displaystyle \frac{15\omega LI_5}{\sqrt{R^2 + 225\omega^2 L^2}}\) | (ソ) | \(\displaystyle \frac{9\omega LI_3}{\sqrt{R^2 + 81\omega^2 L^2}}\) |
| (ツ)(6) | \(\displaystyle \frac{RI_5}{\sqrt{R^2 + 225\omega^2 L^2}}\) | (ネ) | \(27\omega LI_3\) |
出典:令和6年度第一種電気主任技術者理論科目B問題問5
解説
内容自体は難しくはないのですが、実際に試験でこれを見るとまず問題の内容を理解するのに時間をとられ、また後半の問題なので残り時間も少なくなっており焦りを感じることになると思います。
問題10問に対して解答群は20個ですから、選択肢を絞りやすく冷静に考えれば高得点を狙える問題ではあります。
・他の計算不要な問題を早く解き時間に余裕をもたせる
・問題の全体像が分からなくても解答できる問題は確実に拾う
等、意識したいところです。
抵抗\( R \)の結線
サービス問題です。当然\(\Delta\)結線です。
~が全て開放され電圧源のみがある回路A
ここもサービス問題で、当然電流源です。
電圧源のが全て~され電流源のみがある回路B
これもサービス問題で、当然短絡です。文脈でも分かるかと思います。
5次の高調波電流三相分の和
後の問題文に「には流れない」とあることから、0であると推測できます。計算過程は以下のようになります。
\begin{aligned} &\sqrt{2}I_{5} \sin 5\omega t + \sqrt{2}I_{5} \sin \left( 5\omega t + \frac{2}{3}\pi \right) + \sqrt{2}I_{5} \sin \left( 5\omega t - \frac{2}{3}\pi \right) \\ =&\sqrt{2}I_{5} \sin 5\omega t + \sqrt{2}I_{5} \left( \sin 5\omega t \cos \frac{2}{3}\pi + \cos 5\omega t \sin \frac{2}{3}\pi \right) + \sqrt{2}I_{5} \left( \sin 5\omega t \cos \frac{2}{3}\pi - \cos 5\omega t \sin \frac{2}{3}\pi \right) \\ =&\sqrt{2}I_{5} \sin 5\omega t + \sqrt{2}I_{5} \left( -\frac{1}{2}\sin 5\omega t + \frac{\sqrt{3}}{2}\cos 5\omega t \right) + \sqrt{2}I_{5} \left( -\frac{1}{2}\sin 5\omega t -\frac{\sqrt{3}}{2} \cos 5\omega t \right) \\ =& \sqrt{2}I_{5} \sin 5\omega t - \sqrt{2}I_{5} \sin 5\omega t \\ =& 0 \end{aligned}
5次の高調波電流三相分の和が流れないところ
5次の高調波が全て流れるところ( \(=0\) )が答えになるので、中性点 \(N_2\) の接地線です。
電圧源側へ戻る5次電流成分の大きさ(実効値)
簡単な解き方は負荷を\( \Delta - Y \)変換することです。
回路は対称なため、各相の電流は同じように分流します。そうすると、5次の高調波電流三相分の和は0であることが分かっているため、図のようになり、別の相の高調波電流を考慮しなくていいことが分かります。
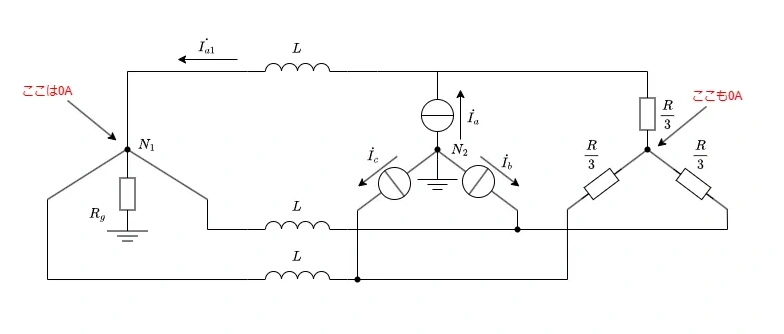
一相分の等価回路は以下のようになり、これの\(\dot{I_{a1}}\)の大きさが答えです。
なお、5次の高調波なので誘導性リアクタンスは5倍になることに気を付ける必要があります。
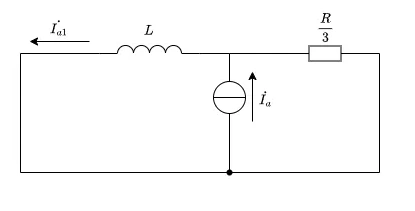
5次の高調波の実効値は\(I_5\)なので、分流の法則より
\begin{aligned} |\dot{I_{a1}}| &= \frac{\frac{R}{3}}{\sqrt{\left(\frac{R}{3}\right)^2 + (5\omega L)^2}} I_5 \\ &=\frac{RI_5}{\sqrt{R^2 + 225\omega^2 L^2}} \\ \end{aligned}
電圧源側へ戻る5次電流成分による高調波発生源の対地電圧の5次成分の大きさ(実効値)
\(R_g\)には5次の電流は流れていないため、これによる対地電圧は考慮する必要がありません。
よって、対地電圧はリアクタンスにかかる電圧の大きさに等しく、(6)の答えに\(5\omega L\)をかけたものになるので
\begin{aligned} \frac{5\omega LRI_5}{\sqrt{R^2 + 225\omega^2 L^2}} \end{aligned}
で表されます。
電圧源側へ戻る3次電流成分の大きさ(実効値)
3次の高調波は各相同相なので、その合計は
\( \displaystyle \sqrt{2}I_{3} \sin 3\omega t + \sqrt{2}I_{3} \sin 3\omega t + \sqrt{2}I_{3} \sin 3\omega t = 3\sqrt{2}I_{3} \sin 3\omega t\)
となります。電流の合計が0ではないため、これはどこかを通って中性点\(N_2\)を流れるわけですが、それは接地抵抗\(R_g\)しかありません。
電圧源側へ戻る3次電流成分の大きさ(実効値)は、回路が対称なので各相等しくなり、一相分は\( \displaystyle \sqrt{2}I_{3} \sin 3\omega t \)であり、その実効値は\(I_3\)です。
各電流源の3次電流成分が\( \displaystyle \sqrt{2}I_{3} \sin 3\omega t \)で、電圧源側に戻る電流も\( \displaystyle \sqrt{2}I_{3} \sin 3\omega t \)なので、問題文にある通り負荷側には電流は流れません。
電圧源の中性点から接地抵抗\(R_g\)を経て大地へ流れる3次電流成分の大きさ(実効値)
上記の通り、\(R_g\)を流れる3次電流成分は\( \displaystyle3\sqrt{2}I_{3} \sin 3\omega t\)なので、その実効値は\( \displaystyle 3I_{3} \)です。
高調波発生源の対地電圧の3次成分の大きさ(実効値)
(7)と違い中性点\(N_1\)にも電流が流れているため、これも考慮する必要があります。
中性点の電流の大きさは\( \displaystyle 3I_{3} \)であること、誘導性リアクタンスは3倍になることに注意して対地電圧を求めると
\( \displaystyle 3R_g I_{3} + j3\omega LI_{3}\)
となり、その大きさは
\(\displaystyle 3I_3\sqrt{R_g^2 + \omega^2 L^2}\)
となります。
参考
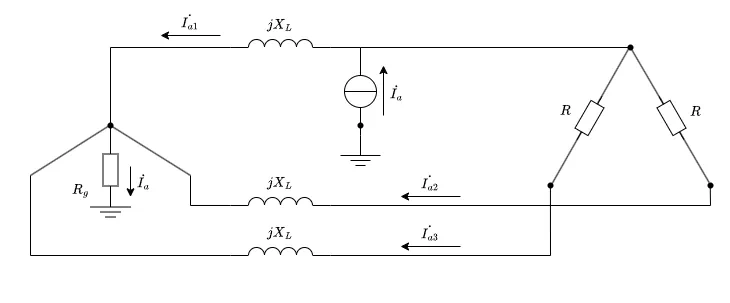
\( \Delta - Y \)変換しない場合、下の画像を各相分計算して合計してください。
これだけですと\(\dot{I_{a1}}\)は\(\displaystyle \left( \frac{R}{R+j3X_L}+\frac{jX_L}{R+j3X_L} \right)・ \sqrt{2}I_{5} \sin 5\omega t \)となりますが、各相合計すると\(\displaystyle \left( \frac{R}{R+j3X_L}\right)・ \sqrt{2}I_{5} \sin 5\omega t \)となり、\( \Delta - Y \)変換した結果と一致します。
- (1)ホ \(\Delta\)
- (2)ト 電流源
- (3)ニ 短絡
- (4)ヲ 0
- (5)ハ 中性点 \(N_2\) の接地線
- (6)ツ \(\displaystyle \frac{RI_5}{\sqrt{R^2 + 225\omega^2 L^2}}\)
- (7)ヨ \(\displaystyle \frac{5\omega LRI_5}{\sqrt{R^2 + 225\omega^2 L^2}}\)
- (8)リ \(I_3\)
- (9)チ \(3I_3\)
- (10)ワ \(\displaystyle 3I_3\sqrt{R_g^2 + \omega^2 L^2}\)