電験一種 R6年 理論 問4
次の文章は、電気回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
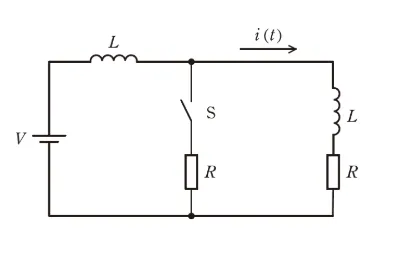
図の回路は、電圧\(V\)の直流電圧源、スイッチS, 抵抗\(R\)及びインダクタンス\(L\)のインダクタから構成されており、二つのインダクタ間には相互誘導はないものとする。
時刻 \(t<0\) ではスイッチSは閉じており、回路は定常状態にある。\(t=0\)でスイッチSを開くこととする。\(t\geqq0\)における回路の電流を\(i(t)\)とすれば、\(t\geqq0\)において次式の回路方程式が成り立つ。
(1)\(=V\)・・・・・・・・・・・・・・①
スイッチSを開く直前と直後において二つのインダクタによる磁束の和は不変であるので、スイッチSを開いた直後の電流を\(i(0)\)とすれば、スイッチSを開く直前と直後における二つのインダクタによる磁束に関して次式が成り立つ。
(2)\(=2Li(0)\)
また、①式の回路方程式の定常解を\(i_S(t)\)、過渡解を\(i_T(t)\)とすれば、\(K\)を任意定数として、
\(i_S(t)=\)(3)
\(i_T(t)=\)(4)
となる。
回路方程式の定常解\(i_S(t)\)と過渡解\(i_T(t)\)、及びスイッチSを開いた直後の電流\(i(0)\)の条件より、\(t\geqq0\)における\(i(t)\)は次式となる。
\(i(t)=\)(5)
| (イ) | \( \displaystyle \frac{2LV}{R} \) | (ロ) | \( \displaystyle \frac{V}{2R} + \frac{V}{R} e^{-\frac{2R}{L}t} \) | (ハ) | \( \displaystyle \frac{V}{R} - \frac{V}{2R} e^{-\frac{R}{2L}t} \) |
| (ニ) | \( L \displaystyle \frac{di(t)}{dt} + 2Ri(t) \) | (ホ) | \( \displaystyle \frac{2V}{R} \) | (ヘ)(3) | \( \displaystyle \frac{V}{R} \) |
| (ト)(4) | \( Ke^{-\frac{R}{2L}t} \) | (チ) | \( Ke^{-\frac{R}{L}t} \) | (リ)(2) | \( \displaystyle \frac{3LV}{R} \) |
| (ヌ) | \( L \displaystyle \frac{di(t)}{dt} + Ri(t) \) | (ル)(1) | \( 2L \displaystyle \frac{di(t)}{dt} + Ri(t) \) | (ヲ)(5) | \( \displaystyle \frac{V}{R} + \frac{V}{2R} e^{-\frac{R}{2L}t} \) |
| (ワ) | \( Ke^{-\frac{2R}{L}t} \) | (カ) | \( \displaystyle \frac{V}{2R} \) | (ヨ) | \( \displaystyle \frac{LV}{R} \) |
出典:令和6年度第一種電気主任技術者理論科目A問題問4
解説
(2)がやや理解しにくいところではありますが、ここを間違えても後半を解くことは可能です。
この問題は理屈が分かっていれば式を立てることなく解くことが可能です。理論は時間がないのでこのような問題は本番では計算を極力せず終わらせたいところです。
スイッチSを開いた時の回路方程式
スイッチSを開いた後は図のようにインダクタ2つと抵抗1つの回路となります。
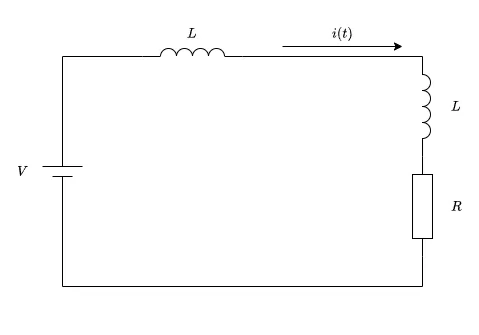
よって
\( 2L \displaystyle \frac{di(t)}{dt} + Ri(t)=V \)
です。
スイッチSを開く直前と直後における二つのインダクタによる磁束
スイッチSを開く前、定常状態における電流は、インダクタは短絡とみなせるため図のようになります。
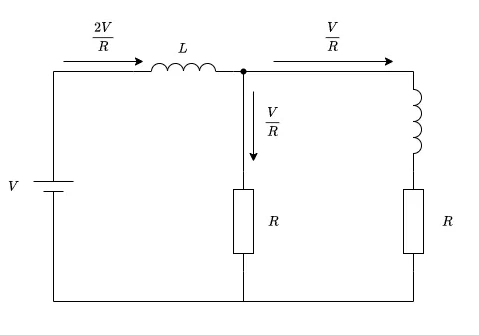
インダクタと磁束の関係は\( NΦ=LI \)で表されるので、全体の磁束は
\(\displaystyle L \frac{2V}{R} + L \frac{V}{R} = \frac{3LV}{R} =2Li(0)\)
となります。また、これより
\(\displaystyle i(0) = \frac{3V}{2R} \)
となります。※(5)で使用
定常解\(i_S(t)\)
定常解は\(\displaystyle \frac{di(t)}{dt} = 0 \)とした時の回路方程式の解なので、
\( Ri_S(t)=V \)
より
\( \displaystyle i_S(t)=\frac{V}{R} \)
となります。
過渡解\(i_T(t)\)
過渡解は\(V = 0 \)とした時の回路方程式の解なので、
\(\displaystyle 2L\frac{di_T(t)}{dt} + Ri_T(t) = 0\)
これを解けばいいのですが、計算しなくとも答えは出せます。
最終的に0になる解答の選択肢は(ト)(チ)(ワ)しかありません。
3つの選択肢の違いは時定数であり、スイッチを開いた後はインダクタ2つと抵抗1つの回路になるわけですから、インダクタンスは\(2L\)で答えは\( Ke^{-\frac{R}{2L}t} \)となります。
以下、解き方ですが本番では非推奨です。変数分離して両辺を積分します。
\begin{aligned} 2L\frac{di_T(t)}{dt} + Ri_T(t) &= 0 \\ 2L\frac{di_T(t)}{dt} &= -Ri_T(t) \\ \frac{di_T(t)}{i_T(t)} &= -\frac{R}{2L}dt\\ \int \frac{ di_T(t)}{i_T(t)} &= -\frac{R}{2L}\int dt \\ log_{ e } |i_T(t)| &= -\frac{R}{2L} t + C \quad (C \text{ は積分定数}) \\ i_T(t) &=\pm e^{-\frac{R}{2L} t+C} \\ &= \pm e^Ce^{-\frac{R}{2L} t} \\ &= Ke^{-\frac{R}{2L} t} \quad (K = \pm e^C) \end{aligned}
\(t\geqq0\)における\(i(t)\)
一般解\(i(t)\)は
\begin{aligned} i(t) &= i_S(t) + i_T(t) \\ &= \frac{V}{R} + Ke^{-\frac{R}{2L}t} \end{aligned}
で表されます。ここに、(2)で求めた\(\displaystyle i(0) = \frac{3V}{2R} \)を満たすような任意定数\(K\)を決めます。
\(t=0\)のとき、
\begin{aligned} \frac{3V}{2R} &= \frac{V}{R} + K \end{aligned}
ですから、
\begin{aligned} K &= \frac{V}{2R} \end{aligned}
となるので、\(t\geqq0\)における\(i(t)\)は
\begin{aligned} i(t) &= \frac{V}{R} + \frac{V}{2R}e^{-\frac{R}{2L}t} \end{aligned}
となります。
なお、\(t=\infty\)の時\(\displaystyle i(\infty) = \frac{V}{R} \)にならないといけないことは(3)より明らかであり、この時点で応えは(ハ)か(ヲ)となります。※(ロ)は時定数も違う
\(t=0\)の時、(ハ)は\(\displaystyle \frac{V}{2R} \)、(ヲ)は\(\displaystyle \frac{3V}{2R} \)となります。
これが\(i(0)\)にあたるので、(2)にあてはめてみると(ハ)の場合は\(\displaystyle \frac{LV}{R} \)、(ヲ)の場合は\(\displaystyle \frac{3LV}{R} \)となります。 (ハ)は各インダクタに流れていた電流を考えると、磁束の和としては不適です。 よって、消去法により答えは(ヲ)となります。
また、スイッチSを開く前に流れていた電流によりインダクタにエネルギーが蓄えられているはずなのに、電流値が元の\(\displaystyle \frac{V}{R} \)より小さくなる(ハ)はおかしいという考え方でも答えを出すことは可能かと思います。 これができれば、逆にここから(2)に戻って答えを導くことが可能です。
- (1)ル \( 2L \displaystyle \frac{di(t)}{dt} + Ri(t) \)
- (2)リ \( \displaystyle \frac{3LV}{R} \)
- (3)ヘ \( \displaystyle \frac{V}{R} \)
- (4)ト \( Ke^{-\frac{R}{2L}t} \)
- (5)ヲ \( \displaystyle \frac{V}{R} + \frac{V}{2R} e^{-\frac{R}{2L}t} \)