電験一種 R6年 理論 問3
次の文章は,直流回路の消費電力に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
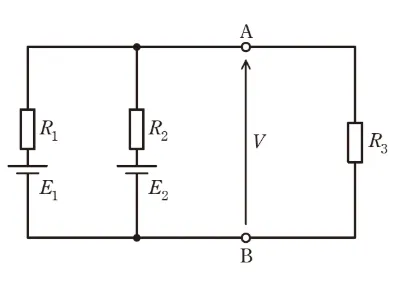
電圧\(E_1\), \(E_2\)の直流電圧源及び抵抗\(R_1\), \(R_2\), \(R_3\)で構成される回路における\(R_3\)の消費電力\(P\)を求めたい。図中の端子A-B間の電圧を\(V\)とすれば,\(\displaystyle P=\frac{V^2}{R_3}\)なので,まずは\(V\)を求めてみる。
最初に,図の電圧源を短絡除去した回路を考えて,端子A-B間から見た回路全体のコンダクタンスを求めると(1)となる。次に,図の端子A-B間を短絡した回路を考えて,端子Bから\(R_1\)及び\(R_2\)を介して端子Aに流れる電流を求めると(2)となる。ここで,上記のように求めたコンダクタンス及び電流を用いて次式のように\(V\)を求めることができる。
\(\displaystyle V = \frac{\class{anaume}{(2)}}{\class{anaume}{(1)}}\)
このように,直列接続された電圧源と抵抗が複数並列接続された回路の電圧を求める定理は(3)の定理と呼ばれる。
次に,\(P\)が最大になるような\(R_3\)の値を求めてみる。消費電力が最大になるのは,図の電圧源を短絡除去した回路を考えて,端子A-Bから見た左側の合成抵抗が\(R_3\)と等しい場合である。したがって,\(R_3=\)(4)を満足するとき,最大電力が(5)となる。
| (イ) | テブナン | (ロ) | ジュール | (ハ)(3) | ミルマン |
| (ニ) | \(\displaystyle \frac{R_1+R_2}{R_1R_2}\) | (ホ) | \(\displaystyle \frac{E_2}{R_1} + \frac{E_1}{R_2}\) | (ヘ)(2) | \(\displaystyle \frac{E_1}{R_1} + \frac{E_2}{R_2}\) |
| (ト)(4) | \(\displaystyle \frac{R_1R_2}{R_1+R_2}\) | (チ)(1) | \(\displaystyle \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\) | (リ) | \(\displaystyle \frac{R_3}{R_1R_2}\) |
| (ヌ) | \(R_1E_1 + R_2E_2\) | (ル) | \(R_1 + R_2\) | (ヲ) | \(R_1 + R_2 + R_3\) |
| (ワ) | \(\displaystyle \frac{(R_2E_1 + R_1E_2)^2}{2R_1R_2(R_1+R_2)}\) | (カ)(5) | \(\displaystyle \frac{(R_2E_1 + R_1E_2)^2}{4R_1R_2(R_1+R_2)}\) | (ヨ) | \(\displaystyle \frac{R_2E_1 + R_1E_2}{4R_1R_2(R_1+R_2)}\) |
出典:令和6年度第一種電気主任技術者理論科目A問題問3
解説
一種の理論の中では簡単な問題かと思います。
(1)で並列回路に\( R_3 \)を入れないミスが考えられるかなと思います。解いているうちに気付くとは思いますが。
端子A-B間から見た回路全体のコンダクタンス
電圧源を短絡除去した上で端子A-B間から見た合成コンダクタンス\( G \)は、図の通り\( R_1 \)、\( R_2 \)、\( R_3 \)の並列回路であることから各コンダクタンスの和です。
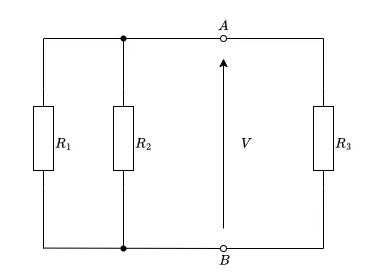
よって
\(\displaystyle G = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\)
です。
端子Bから\( R_1 \)及び\( R_2 \)を介して端子Aに流れる電流
A-B間を短絡していることから、各電圧源による電流は全て短絡している箇所を流れますので、図のようになり
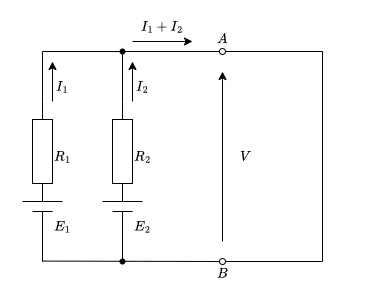
電流は
\(\displaystyle \frac{E_1}{R_1} + \frac{E_2}{R_2}\)
となります。
定理の名前
問題文で与えられた式に(1)、(2)を入れると
\( \displaystyle V = \frac{\displaystyle \frac{E_1}{R_1} + \displaystyle \frac{E_2}{R_2}}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \frac{1}{R_3}} \)
となります。
このように、直列接続された電圧源と抵抗が複数並列接続された回路の電圧を求める定理をミルマンの定理といいます。ミルマンの定理を知らなくても今回の問題なら消去法で解けるかと思います。
ミルマンの定理はこのような式で表せます。
\( \displaystyle V_0 = \frac{\displaystyle \sum_{i=1}^{N} Y_i V_i}{\displaystyle \sum_{i=1}^{N} Y_i} \)
\( Y \)はアドミタンス、\( V \)は各電圧源の電圧です。今回の問題では\( R_3 \)に電圧源は存在しませんので、\( V_3 = 0 \)として考えます。
消費電力が最大になる抵抗\( R_3 \)
理屈はさておき、問題文に従えば
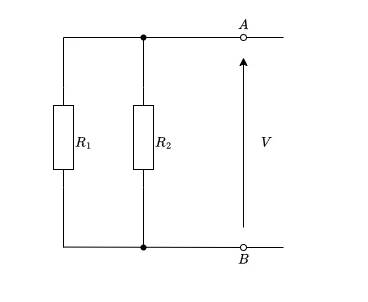
これの左側の合成抵抗が\(\displaystyle \frac{R_1R_2}{R_1+R_2}\)なのは自明かと思います。
最大電力\( P \)
\(\displaystyle P=\frac{V^2}{R_3}\)なので、まずは\( V \)を求めます。
\begin{aligned} \displaystyle V &= \frac{\displaystyle \frac{E_1}{R_1} + \displaystyle \frac{E_2}{R_2}}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \frac{1}{R_3}} \\ &= \frac{\displaystyle \frac{E_1}{R_1} + \displaystyle \frac{E_2}{R_2}}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \frac{R_1+R_2}{R_1R_2}} \\ &= \frac{\displaystyle \frac{E_1}{R_1} + \displaystyle \frac{E_2}{R_2}}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \frac{R_1+R_2}{R_1R_2}} ・ \displaystyle \frac{R_1R_2}{R_1R_2} \\ &= \frac{E_1 R_2 + E_2 R_1}{2(R_1 + R_2)} \\ \end{aligned}
これを二乗すれば分母に4が出るので、答えは(カ)になることが分かります。(ヨ)は次元が電力ではありません。
答えを求めると
\begin{aligned} \displaystyle P &=\frac{V^2}{R_3}\\ &= \left\{ \frac{E_1 R_2 + E_2 R_1}{2(R_1 + R_2)} \right\}^2 ・\frac{R_1+R_2}{R_1R_2} \\ &= \displaystyle \frac{(R_2E_1 + R_1E_2)^2}{4R_1R_2(R_1+R_2)} \\ \end{aligned}
となります。
参考
最大電力となる\(R_3\)を求めます。
\begin{aligned} \displaystyle P &= \left( \frac{\displaystyle \frac{E_1}{R_1} + \displaystyle \frac{E_2}{R_2}}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \frac{1}{R_3}} \right)^2 ・ \frac{1}{R_3} \\ &= \left( \frac{E_1 R_2 + E_2 R_1}{\displaystyle \frac{(R_1 + R_2)R_3 + R_1 R_2}{R_3}} \right)^2 \cdot \displaystyle \frac{1}{R_3} \\ &= \frac{(E_1 R_2 + E_2 R_1)^2 R_3^2}{\left\{ (R_1 + R_2)R_3 + R_1 R_2 \right\}^2} \cdot \frac{1}{R_3} \\ &= \frac{(E_1 R_2 + E_2 R_1)^2 R_3}{(R_1 + R_2)^2 R_3^2 + 2(R_1 + R_2)R_1 R_2 R_3 + (R_1R_2)^2} \\ &= \frac{(E_1 R_2 + E_2 R_1)^2}{(R_1 + R_2)^2 R_3 + 2(R_1 + R_2)R_1 R_2 + \displaystyle \frac{(R_1R_2)^2}{R_3}} \\ \end{aligned}
分母にのみ\( R_3 \)がある形になりましたので、これを\( Y \)とおいて\( R_3 \)で微分します。
\( Y = (R_1 + R_2)^2 R_3 + 2(R_1 + R_2)R_1 R_2 + \displaystyle \frac{(R_1R_2)^2}{R_3} \)
\(\displaystyle \frac{dY}{dR_3} = (R_1 + R_2)^2 - \displaystyle \frac{(R_1 R_2)^2}{R_3^2} \)
\(\displaystyle \frac{dY}{dR_3} = 0 \)となるときの\( R_3 \)を求めます。
\begin{aligned} 0 &= (R_1 + R_2)^2 - \displaystyle \frac{(R_1 R_2)^2}{R_3^2} \\ (R_1 + R_2)^2 &= \frac{(R_1 R_2)^2}{R_3^2} \\ R_3^2 &= \frac{(R_1 R_2)^2}{(R_1 + R_2)^2}\\ R_3 &= \pm \frac{R_1 R_2}{R_1 + R_2}\\ \end{aligned}
\( R_3 \)は正の値なので、
\(\displaystyle R_3 = \frac{R_1 R_2}{R_1 + R_2} \)
次に、この\( R_3 \)が\( Y \)を最小化することを示します。\(\displaystyle \frac{d^2Y}{dR_3^2} \)を計算します。
\(\displaystyle \frac{d^2Y}{dR_3^2} = \frac{2(R_1 R_2)^2}{R_3^3} \)
\( R_1 \),\( R_2 \),\( R_3 \)は正の値なので、\(\displaystyle \frac{d^2Y}{dR_3^2} > 0 \)となり、\(Y\)は極小値を持つことがわかります。\( Y \)は分母なので、このとき\( P \)は最大となります。
- (1)チ \(\displaystyle \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\)
- (2)ヘ \(\displaystyle \frac{E_1}{R_1} + \frac{E_2}{R_2}\)
- (3)ハ ミルマン
- (4)ト \(\displaystyle \frac{R_1R_2}{R_1+R_2}\)
- (5)カ \(\displaystyle \frac{(R_2E_1 + R_1E_2)^2}{4R_1R_2(R_1+R_2)}\)