電験一種 R6年 理論 問2
次の文章は、円形コイルの作る磁界に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
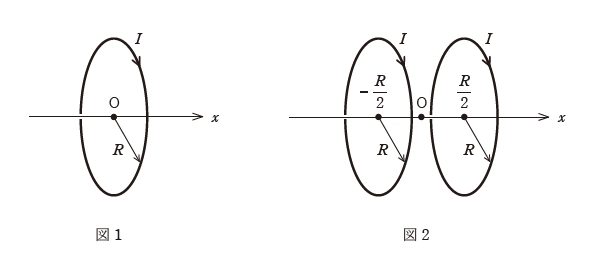
真空中において半径 \(R\) で一巻きの円形コイルに電流 \(I\) が流れている。図1のように \(x\) 軸の原点 O に円形コイルの中心があり、\(x\) 軸上に正の向きの磁束を生じるように置かれているときの \(x\) 軸上の磁束密度の大きさ \(B(x)\) は、ビオ・サバールの法則により次のように求められる。ただし、\(\mu_0\) は真空中の透磁率である。
\(\displaystyle B(x) = \frac{\mu_0 I R^2}{2(x^2 + R^2)^{\frac{3}{2}}}\)
次に、この円形コイル二つを図2のように原点 O に対称に距離 \(R\) だけ離して置く。このコイルをヘルムホルツコイル (Helmholtz coil) という。ここで、ヘルムホルツコイルの \(x\) 軸上の磁束密度の大きさ \(B_H(x)\) について考察する。
\(B_H(x)\) を \(B(x)\) で表すと、(1) である。
ここで、\(B_H(x)\) を次のようにマクローリン展開することを考える。ただし、\(B_H^{(n)}(x)\) は \(B_H(x)\) の \(n\) 階微分を表す。
\(\displaystyle B_H(x) = B_H(0) + B_H'(0)x + \frac{B_H''(0)}{2!}x^2 + \cdots + \frac{B_H^{(n)}(0)}{n!}x^n + \cdots\)
まず、\(x\) の2乗の項を取り出して考えると、\(B_H''(0) = \)(2) である。
関数 \(\displaystyle f(x) = \frac{1}{(x^2 + a^2)^{\frac{3}{2}}}\) について、\(\displaystyle f''(x) = \frac{12x^2 - 3a^2}{(x^2 + a^2)^{\frac{7}{2}}}\) である。
一方、\(B(x)\) は \(B(-x) = B(x)\) が成り立つため、偶関数である。したがって、\(B_H(x)\) は (3) である。このため、\(x\) の奇数乗の項は全てゼロとなる。
これまでの考察で、マクローリン展開した項のうち、定数項を除き、\(x\) の (4) の項までがゼロになることが分かった。このことから、ヘルムホルツコイルを用いると原点近傍で (5) 磁界が得られることが分かる。
| (イ) | \(x\)に比例する | (ロ) | 急峻に変化する | (ハ)(5) | ほぼ一定の |
| (ニ) | 1乗 | (ホ) | 2乗 | (ヘ)(4) | 3乗 |
| (ト) | 奇関数 | (チ)(3) | 偶関数 | (リ)(2) | 0 |
| (ヌ) | \(\displaystyle \frac{144\sqrt{2}}{R^3}\mu_0 I\) | (ル) | \(\displaystyle \frac{216}{R^3}\mu_0 I\) | (ヲ) | \(B(x+R)+B(x-R)\) |
| (ワ) | \(\sqrt{2}B(x)\) | (カ) | \(2B(x)\) | (ヨ)(1) | \(\displaystyle B\left(x+\frac{R}{2}\right)+B\left(x-\frac{R}{2}\right)\) |
出典:令和6年度第一種電気主任技術者理論科目A問題問2
解説
過去問にないタイプの問題です。数学力があれば問題ないですが、ないと問題を理解するところで手間取ると思います。一応冷静に考えれば知識がなくてもある程度は解けると思います。ただ理論は時間足りなくなりがちです。
\(B_H(x)\) を \(B(x)\) で表す
与えられた式に\(x=0\)を代入すると\(\displaystyle B(0) = \frac{\mu_0 I}{2R}\) になります。
左のコイルでは\(\displaystyle x=-\frac{R}{2}\)の時に\(\displaystyle \frac{\mu_0 I}{2R}\)にならないといけないので、
\(\displaystyle B(x+\frac{R}{2}) \)
となります。同様に、右のコイルでは\(\displaystyle x=\frac{R}{2}\)の時に\(\displaystyle \frac{\mu_0 I}{2R}\)にならないといけないので、
\(\displaystyle B(x-\frac{R}{2}) \)
となります。電流の向きが同じであることから、\(B_H(x)\)はこれらの和となりますので、
\(\displaystyle B_H(x) = B(x+\frac{R}{2}) + B(x-\frac{R}{2}) \)
となります。
\(B_H''(0) \)
問題にて二階微分の計算結果が与えられています。それより、\(\displaystyle B''(x) = \frac{\mu_0 I R^2 (12x^2 - 3R^2)}{2(x^2 + R^2)^{\frac{7}{2}}} \)です。
\(B_H''(0) \)は
\begin{aligned} B_H''(0) = B''\left(\frac{R}{2}\right) + B''\left(-\frac{R}{2}\right) \end{aligned}
となりますので、\(\displaystyle B''(\frac{R}{2})\)と\(\displaystyle B''(-\frac{R}{2})\)をそれぞれ計算しますと
\begin{aligned} B''\left(\frac{R}{2}\right) &= \frac{\mu_0 I R^2 \left\{12\left(\frac{R}{2}\right)^2 - 3R^2\right\}}{2\left\{\left(\frac{R}{2}\right)^2 + R^2\right\}^{7/2}}\\ &= \frac{\mu_0 I R^2 (3R^2 - 3R^2)}{2\left(\frac{R^2}{4} + R^2\right)^{7/2}}\\ &= 0\\ \end{aligned}
\begin{aligned} B''\left(-\frac{R}{2}\right) &= \frac{\mu_0 I R^2 \left\{12\left(-\frac{R}{2}\right)^2 - 3R^2\right\}}{2\left\{\left(-\frac{R}{2}\right)^2 + R^2\right\}^{7/2}}\\ &= \frac{\mu_0 I R^2 (3R^2 - 3R^2)}{2\left(\frac{R^2}{4} + R^2\right)^{7/2}}\\ &= 0\\ \end{aligned}
よって
\(B_H''(0) =0 \)
です。
\(B_H(x) \)は偶関数か奇関数か
偶関数: \(f(-x)=f(x)\)を満たす関数。y軸に関して対称なグラフを持ちます。
奇関数: \(f(-x)=-f(x)\) を満たす関数。原点に関して対称なグラフを持ちます。
\begin{aligned} B(x) &= \frac{\mu_0 I R^2}{2(x^2 + R^2)^{\frac{3}{2}}} \\ B(-x) &= \frac{\mu_0 I R^2}{2\left\{(-x)^2 + R^2\right\}^{\frac{3}{2}}} = \frac{\mu_0 I R^2}{2(x^2 + R^2)^{\frac{3}{2}}} = B(x) \\ \end{aligned}
問題文にある通り、\(B(x) \)は偶関数であることが分かります。
偶関数と偶関数の和は偶関数なので、
\begin{aligned} B_H(-x) &= B\left(-x + \frac{R}{2}\right) + B\left(-x - \frac{R}{2}\right)\\ &= B\left(x - \frac{R}{2}\right) + B\left(x + \frac{R}{2}\right) \\ &= B\left(x + \frac{R}{2}\right) + B\left(x - \frac{R}{2}\right)\\ &= B_H(x) \end{aligned}
です。よって\(B_H(x)\)は偶関数です。
問題解く上では必ずしも必要ではないですが、\(x\)の奇数乗の項は全てゼロになることについて。
偶関数は微分すると奇関数になります。
微分の定義
\begin{aligned} f'(x) &= \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}\\ \end{aligned}
\( f'(-x) \)を計算。偶関数の定義より、\( f(−x+h)=f(x−h) \) および\() f(−x)=f(x) \)なので、
\begin{aligned} f'(-x) &= \lim_{h \to 0} \frac{f(-x + h) - f(-x)}{h}\\ &= \lim_{h \to 0} \frac{f(x - h) - f(x)}{h}\\ \end{aligned}
分母と分子にマイナスをかけます
\begin{aligned} f'(-x) &= -\lim_{h \to 0} \frac{f(x + (-h)) - f(x)}{-h}\\ f'(-x) &= -f'(x)\\ \end{aligned}
奇関数は原点に対して対称な関数であり、\(f'(0)=0 \)となります。
奇関数を微分すると偶関数になり、偶関数を微分すると奇関数になるので\(x\)の奇数乗の項は奇関数になります。
\(x\)の0になる項
今までの解答により、\(B_H'(0) \)、\(B_H''(0) \)、\(B_H'''(0) \)が0になることが分かりましたので、\(x\)の3乗の項までが0になります。
原点近傍で得られる磁界
\(x^4\)以降の項は\(x\)が小さい範囲では影響は小さいため、原点近傍では定数項のみとなりほぼ一定の磁界が得られることが分かります。
- (1)ヨ \(\displaystyle B\left(x+\frac{R}{2}\right)+B\left(x-\frac{R}{2}\right)\)
- (2)リ 0
- (3)チ 偶関数
- (4)ヘ 3乗
- (5)ハ ほぼ一定の