電験一種 R6年 理論 問1
次の文章は,三つの同心導体球殻A,B,C上の電荷と電位に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
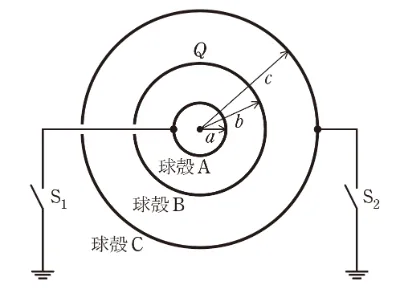
図のように,球殻A,B,Cは同心となるように真空中(誘電率\(\epsilon_0\))に置かれている。それぞれの半径はa,b,cであり,球殻の厚さは無視できる。また,各球殻の初期電荷は零である。球殻B及びCには穴が開けられて導線が引き出されており,スイッチ\(S_1\)を閉じることで球殻Aを接地できる。また,スイッチ\(S_2\)を閉じることで球殻Cを接地できる。穴は十分小さく,かつ導線及びスイッチは周りの空間と絶縁されており,その影響は無視できる。
\(S_1\)及び\(S_2\)が共に開いている状態で,球殻Bに電荷\(Q\)を与える場合,無限遠を接地電位(零)としたときの球殻Aの電位は(1)となる。
\(S_1\)のみを閉じている状態で,球殻Bに電荷\(Q\)を与える場合,球殻Aに電荷(2)が生じ,無限遠を接地電位(零)としたときの球殻Bの電位は(3)となる。これより,球殻Bの対地静電容量を(4)と求めることができる。
\(S_1\)と\(S_2\)を共に閉じている状態で球殻Bに電荷\(Q\)を与える場合,球殻Cの電荷は(5)となる。
| (イ) | \(Q\) | (ロ) | \(-Q\) | (ハ) | \(0\) |
| (ニ) | \(\displaystyle -\frac{(c-b)a}{(c-a)b}Q\) | (ホ) | \(\displaystyle \frac{(b-a)Q}{4\pi\epsilon_0 a^2}\) | (ヘ)(5) | \(\displaystyle -\frac{(b-a)c}{(c-a)b}Q\) |
| (ト) | \(4\pi\epsilon_0 b\) | (チ) | \(\displaystyle \frac{(c-b)Q}{4\pi\epsilon_0 bc}\) | (リ)(1) | \(\displaystyle \frac{Q}{4\pi\epsilon_0 b}\) |
| (ヌ) | \(\displaystyle \frac{4\pi\epsilon_0 ab}{b-a}\) | (ル) | \(\displaystyle \frac{Q}{4\pi\epsilon_0 a}\) | (ヲ)(2) | \(\displaystyle -\frac{a}{b}Q\) |
| (ワ)(3) | \(\displaystyle \frac{(b-a)Q}{4\pi\epsilon_0 b^2}\) | (カ) | \(\displaystyle -\frac{(b-a)b}{(c-a)c}Q\) | (ヨ)(4) | \(\displaystyle \frac{4\pi\epsilon_0 b^2}{b-a}\) |
出典:令和6年度第一種電気主任技術者理論科目A問題問1
解説
前半は簡単ですが後半は時間を要するかもしれません。理論は他の科目に比べ時間が足りなくなりやすいので、最初の簡単な問題は確実に解き、後半は選択肢のみ絞りとりあえず解答を記入し、一通り終わった後に残った時間でやるという戦略をとる方がいいかと思います。
無限遠を接地電位(零)としたときの球殻Aの電位
\(S_1\)及び\(S_2\)が共に開いている状態なので、ここは電位に影響を及ぼしません。
また、球殻Bの内側には電荷は存在しないため、球殻Aから球殻Bの間の電界を\(E_A \mathrm {[V/m]} \)とすると、それは0です。
無限遠を基準とした時の球殻Aの電位を\(V_A \mathrm {[V]} \)とすると、それは∞~bとb~aの範囲の電位の合計になるので、球殻Bの外側の電界を\(E_B \mathrm {[V/m]} \)とすると、\(V_A \mathrm {[V]} \)は、中心からの距離を\(r \mathrm {[m]} \)として
\begin{aligned} V_A &= -\int_\infty^b E_B \, dr - \int_b^a E_A \, dr \\ &= - \int_\infty^b E_B \, dr \\ \end{aligned}
となります。ここで、
\(\displaystyle E_B = \frac{Q}{4\pi\epsilon_0 r^2} \)
なので、
\begin{aligned} V_A &= -\int_{\infty}^{b} \frac{Q}{4\pi\epsilon_0 r^2} dr \\ &= -\frac{Q}{4\pi\epsilon_0} \int_{\infty}^{b} \frac{1}{r^2} dr \\ &= -\frac{Q}{4\pi\epsilon_0} \left[-\frac{1}{r}\right]_{\infty}^{b} \\ &= -\frac{Q}{4\pi\epsilon_0} \left(-\frac{1}{b}\right) \\ &= \frac{Q}{4\pi\epsilon_0 b} \end{aligned}
となります。
球殻Aに生じる電荷
\(S_1\)を閉じたことにより、球殻Aは接地されるため\(V_A \mathrm {[V]} \)は\(0 \mathrm {[V]} \)となります。
よって、それぞれ\(V_{A2}\)、\(E_{B2}\)、\(E_{A2}\)として、以下の式が成り立ちます。
\begin{aligned} V_{A2} &= -\int_\infty^b E_{B2} \, dr - \int_b^a E_{A2} \, dr \\ &= 0 \\ \end{aligned}
球殻Bにもともとあった電荷\(Q\)は変わらないため、この式が成り立つ電荷\(Q_A \mathrm {[C]} \)が球殻Aに生じ、これが(2)の答となります。
この時球殻Bの内側には電荷\(Q\)と電荷\(Q_A\)が存在することになりますので、(1)の\(E_B\)と\(E_{B2}\)は違うことに注意する必要があります。
\(\displaystyle E_{B2} = \frac{Q+Q_A}{4\pi\epsilon_0 r^2} \)
\(\displaystyle E_{A2} = \frac{Q_A}{4\pi\epsilon_0 r^2} \)
\(V_{A2}\)の式より、\(E_{B2}\)と\(E_{A2}\)の積分値の和が0である必要があるため、以下が成り立ちます。
\(\displaystyle -\int_{b}^{a} \frac{Q_A}{4\pi\epsilon_0 r^2} dr = \int_{\infty}^{b} \frac{Q+Q_A}{4\pi\epsilon_0 r^2} dr \)
これを計算すると
\begin{aligned} -\int_{b}^{a} \frac{Q_A}{4\pi\epsilon_0 r^2} dr &= \int_{\infty}^{b} \frac{Q+Q_A}{4\pi\epsilon_0 r^2} dr \\ -\frac{Q_A}{4\pi\epsilon_0} \int_{b}^{a} \frac{1}{r^2} dr &= \frac{Q+Q_A}{4\pi\epsilon_0} \int_{\infty}^{b} \frac{1}{r^2} dr \\ -\frac{Q_A}{4\pi\epsilon_0} \left[-\frac{1}{r}\right]_{b}^{a} &= \frac{Q+Q_A}{4\pi\epsilon_0} \left[-\frac{1}{r}\right]_{\infty}^{b} \\ -\frac{Q_A}{4\pi\epsilon_0} \left( -\frac{1}{a} + \frac{1}{b} \right) &= \frac{Q+Q_A}{4\pi\epsilon_0} \left(-\frac{1}{b}\right) \\ -Q_A \left( -\frac{1}{a} + \frac{1}{b} \right) &= (Q + Q_A) \left( -\frac{1}{b} \right) \\ \end{aligned}
これから\(Q_A\)を求めると、
\begin{aligned} -Q_A \left( -\frac{1}{a} + \frac{1}{b} \right) &= (Q + Q_A) \left( -\frac{1}{b} \right) \\ -Q_A \left( -\frac{1}{a} + \frac{1}{b} \right) + \frac{Q_A}{b} &= -\frac{Q}{b} \\ Q_A \left( \frac{1}{a} - \frac{1}{b} + \frac{1}{b} \right) &= -\frac{Q}{b} \\ \frac{Q_A}{a} &= -\frac{Q}{b} \\ Q_A &= -\frac{a}{b}Q \\ \end{aligned}
無限遠を接地電位(零)としたときの球殻Bの電位
球殻Bの電位を求めるので、積分範囲は∞~bです。
また、(2)より球殻Bの内側には\(Q\)と\(Q_A\)が存在しますので、先にこれの和を求めますと
\begin{aligned} Q + Q_A &= Q-\frac{a}{b}Q\\ &= \frac{b-a}{b}Q \\ \end{aligned}
よって、電界\(E_{B3}\)は
\(\displaystyle E_{B3} = \frac{Q}{4\pi\epsilon_0 r^2} \left(\frac{b-a}{b}\right) \)
無限遠を基準電位とした時の電位\(V_{B3}\)は
\begin{aligned} V_{B3} &= - \int_\infty^b E_{B3} \, dr \\ &= - \int_\infty^b \frac{Q}{4\pi\epsilon_0 r^2} \left(\frac{b-a}{b}\right) \, dr \\ &= - \frac{Q\left(b-a\right)} {4\pi\epsilon_0b} \int_\infty^b \frac{1}{r^2} \, dr \\ &= -\frac{Q\left(b-a\right)} {4\pi\epsilon_0b} \left[-\frac{1}{r}\right]_{\infty}^{b} \\ &= -\frac{Q\left(b-a\right)} {4\pi\epsilon_0b} \left(-\frac{1}{b}\right) \\ &= \frac{Q\left(b-a\right)} {4\pi\epsilon_0b^2} \\ \end{aligned}
球殻Bの対地静電容量
球殻Bに与えらえれている電荷が\(Q\)で、電位が(3)より、
\(\displaystyle V_{B3} = \frac{Q\left(b-a\right)} {4\pi\epsilon_0b^2} \)
なので、静電容量\(C_{B} \mathrm {[F]} \)は
\(\displaystyle C_{B} = \frac{Q}{V_{B3}} = \frac{4\pi\epsilon_0b^2} {b-a} \)
となります。
\(S_1\)と\(S_2\)を共に閉じている状態の球殻Cの電荷
\(S_1\)と\(S_2\)が閉じていることにより、球殻Aと球殻Bは接地されているため球殻Aの電位\(V_{A5} \mathrm {[V]} \)と球殻Cの電位\(V_{C5} \mathrm {[V]} \)はともに\(0 \mathrm {[V]} \)となります。
球殻Bの電荷\(Q\)は変わりません。球殻Aには\(V_{A5} \)が0になるような電荷が生じて、これを\(Q_{A5}\)とします。
球殻Aに生じる電荷は(2)の答えとは違うことに注意してください。
\(V_{C5} \)が\(0 \)ということは、球殻Cに生じた電荷を\(Q_{C5}\)とすると、その内側にある電荷は\(Q\)と\(Q_{A5}\)になるので、以下が成り立ちます。
\(\displaystyle V_{C5} = - \int_\infty^c \frac{Q+Q_{A5}+Q_{C5}}{4\pi\epsilon_0 r^2} \, dr = 0 \)
この結果が成り立つのは、
\(Q+Q_{A5}+Q_{C5} = 0\)
のときなので、\(Q_{C5} = -Q-Q_{A5}\)
であることが分かります。よって、\(Q_{A5}\)を求めれば答えを出せます。
(1)を参考に、無限遠からCの間の電界を\(E_{C5} \)、球殻CからBの間の電界を\(E_{B5} \)、球殻BからAの間の電界を\(E_{A5} \)とすると、\(V_{A5} \)は
\begin{aligned} V_{A5} &= -\int_\infty^c E_{C5} \, dr -\int_c^b E_{B5} \, dr - \int_b^a E_{A5} \, dr \\ &= 0 \end{aligned}
となります。\(E_{C5} \)は\(Q+Q_{A5}+Q_{C5} = 0\)であることから\(0 \)です。
これより、\(E_{B5} \)と\(E_{A5} \)の積分値の和が0になればいいことが分かります。
また、\(E_{B5} \)と\(E_{A5} \)は、各球殻の内側の電荷を考慮すると
\(\displaystyle E_{B5} = \frac{Q+Q_{A5}}{4\pi\epsilon_0 r^2} \)
\(\displaystyle E_{A5} = \frac{Q_{A5}}{4\pi\epsilon_0 r^2} \)
です。以上より、積分範囲が変わるだけで、問題(2)の時と同じように
\(\displaystyle -\int_{b}^{a} \frac{Q_{A5}}{4\pi\epsilon_0 r^2} dr = \int_{c}^{b} \frac{Q+Q_{A5}}{4\pi\epsilon_0 r^2} dr \)
が成り立ちます。これを計算すると
\begin{aligned} -\int_{b}^{a} \frac{Q_{A5}}{4\pi\epsilon_0 r^2} dr &= \int_{c}^{b} \frac{Q+Q_{A5}}{4\pi\epsilon_0 r^2} dr \\ -\frac{Q_{A5}}{4\pi\epsilon_0} \int_{b}^{a} \frac{1}{r^2} dr &= \frac{Q+Q_{A5}}{4\pi\epsilon_0} \int_{c}^{b} \frac{1}{r^2} dr \\ -\frac{Q_{A5}}{4\pi\epsilon_0} \left[-\frac{1}{r}\right]_{b}^{a} &= \frac{Q+Q_{A5}}{4\pi\epsilon_0} \left[-\frac{1}{r}\right]_{c}^{b} \\ -\frac{Q_{A5}}{4\pi\epsilon_0} \left( -\frac{1}{a} + \frac{1}{b} \right) &= \frac{Q+Q_{A5}}{4\pi\epsilon_0} \left(-\frac{1}{b} + \frac{1}{c} \right) \\ -Q_{A5} \left( -\frac{1}{a} + \frac{1}{b} \right) &= (Q + Q_{A5}) \left( -\frac{1}{b} + \frac{1}{c} \right) \\ \end{aligned}
これより\(Q_{A5}\)を求めると
\begin{aligned} -Q_{A5} \left( -\frac{1}{a} + \frac{1}{b} \right) &= (Q + Q_{A5}) \left( -\frac{1}{b} + \frac{1}{c} \right) \\ Q_{A5} \left( \frac{1}{a} - \frac{1}{b} + \frac{1}{b} - \frac{1}{c} \right) &= Q \left( -\frac{1}{b} + \frac{1}{c} \right) \\ Q_{A5} \left( \frac{c-a}{ac} \right) &= Q \left( \frac{b-c}{bc} \right) \\ Q_{A5} &= \frac{(b-c)a}{(c-a)b} Q \\ \end{aligned}
\(Q_{C5} = -Q-Q_{A5}\)なので、
\begin{aligned} Q_{C5} &= -Q-Q_{A5} \\ Q_{C5} &= -Q-\frac{(b-c)a}{(c-a)b} Q \\ Q_{C5} &= -\frac{(c-a)b+(b-c)a}{(c-a)b} Q \\ Q_{C5} &= -\frac{bc-ab+ab-ca}{(c-a)b} Q \\ Q_{C5} &= -\frac{bc-ca}{(c-a)b} Q \\ Q_{C5} &= -\frac{(b-a)c}{(c-a)b} Q \\ \end{aligned}
- (1)リ \(\displaystyle \frac{Q}{4\pi\epsilon_0 b}\)
- (2)ヲ \(\displaystyle -\frac{a}{b}Q\)
- (3)ワ \(\displaystyle \frac{(b-a)Q}{4\pi\epsilon_0 b^2}\)
- (4)ヨ \(\displaystyle \frac{4\pi\epsilon_0 b^2}{b-a}\)
- (5)ヘ \(\displaystyle -\frac{(b-a)c}{(c-a)b}Q\)