電験一種 R5年 理論 問6
次の文章は、半導体の熱電効果に関する記述である。文中の (0) に当てはまる最も適切なものを解答群の中から選べ。
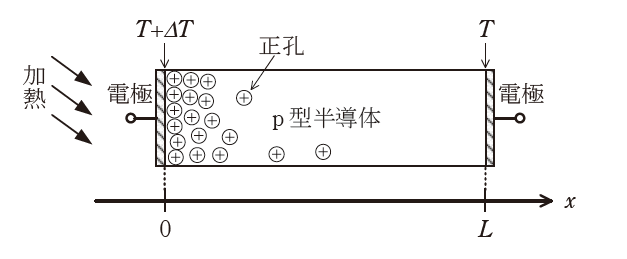
図のように、両端に電極を取り付けた長さ\(L\)のp型半導体を考える。電極端子は開放とする。ここで、左端の電極を加熱したところ、\(x=0\)における半導体の温度が\(T+\Delta T\) \(\left(\Delta T > 0\right)\)に上昇し、右端 \(\left(x=L\right)\) における温度は\(T\)で定常状態になった。左端の温度上昇に伴い、\(x=0\)における正孔濃度が増大することで濃度勾配が生じ、正孔が\(x\)軸の正の方向に拡散する。その結果、右端電極の電位が左端電極に対して\(\Delta V\)だけ上昇する。このように温度差\(\Delta T\)が生じることによって電位差\(\Delta V\)が発生する現象を (1) 効果と呼び、\(\dfrac{\Delta V}{\Delta T}\)は (1) 係数と呼ばれる。以下でこの係数を求めよう。
半導体内の位置\(x\)における正孔濃度を\(p\)、拡散定数を\(D_h\)、正孔の電荷量を\(e(>0)\)とすると、正孔による拡散電流密度は、
\(\displaystyle -eD_h \frac{dp}{dx} \quad \cdots\cdots \)①
と表される。また、半導体内の電界を\(E\)、正孔の移動度を\(\mu_h\)とすると、正孔によるドリフト電流密度は、
\(ep\mu_h E \quad \cdots\cdots \)②
と表される。ただし\(E\)は、\(x\)軸の正方向を正にとるものとする。p型半導体では電子濃度は小さいので電子電流の寄与は無視し、電界\(E\)は半導体内で一定と仮定する。この場合\(E\)は、\(\Delta V\)と\(L\)を用いて、\(E = - \)(2) と表される。両端子が開放されている場合、①式と②式で表される電流密度の総和は0となることから、
\(\displaystyle \frac{dp}{dx} = - \)(3)\( p \quad \cdots\cdots ③\)
が得られる。ただしアインシュタインの関係式\(\displaystyle D_h = \frac{k_BT}{e}\mu_h\)と(2) を用いて、(3) を \(D_h\), \(\mu_h\), \(E\) を用いずに表した。なお\(k_B\)はボルツマン定数を表す。
一方、\(p\) は温度 \(T\) の関数でもあるから、\(\displaystyle \frac{dp}{dx} = \frac{dp}{dT} \frac{dT}{dx}\) と表される。\(\Delta T\) を十分小さいと仮定して\(\displaystyle \frac{dT}{dx} \approx -\frac{\Delta T}{L}\) を代入すると、
\(\displaystyle \frac{dp}{dx} = - \frac{dp}{dT} \frac{\Delta T}{L} \quad \cdots\cdots ④\)
③式と④式の右辺が等しいとおいた式から、\(\displaystyle \frac{\Delta V}{\Delta T}\) を求めると、
\(\displaystyle \frac{\Delta V}{\Delta T} = \)(4)\(\displaystyle \frac{1}{p} \frac{dp}{dT} \quad \cdots\cdots ⑤\)
正孔濃度 \(p\) と温度 \(T\) の関係は、次のように与えられる。
\(p = UT^{\frac{3}{2}} \exp \left( - \dfrac{eV_F}{k_BT} \right) \quad \cdots\cdots ⑥\)
ただし、\(U\), \(V_F\) は定数と仮定する。⑥式を⑤式に代入すると、
\(\displaystyle \frac{\Delta V}{\Delta T} = \)(5)\(\displaystyle + \frac{V_F}{T}\)が得られる。
| (イ) | \(\displaystyle \frac{k_B T}{e} \frac{L}{\Delta V}\) | (ロ) | \(\displaystyle \frac{2}{3} \frac{e}{k_B}\) | (ハ) | \(\displaystyle \frac{L}{\Delta V}\) |
| (ニ) | \(\displaystyle \frac{e}{k_B T}\) | (ホ)(5) | \(\displaystyle \frac{3}{2} \frac{k_B}{e}\) | (ヘ)(1) | ゼーベック |
| (ト)(3) | \(\displaystyle \frac{e}{k_B T} \frac{\Delta V}{L}\) | (チ) | トムソン | (リ) | \(e k_B T\) |
| (ヌ) | \(L \cdot \Delta V\) | (ル) | ペルチエ | (ヲ)(2) | \(\displaystyle \frac{\Delta V}{L}\) |
| (ワ) | \(\displaystyle \frac{2}{3} \frac{k_B}{e}\) | (カ) | \(\displaystyle \frac{k_B T}{e} \frac{\Delta V}{L}\) | (ヨ)(4) | \(\displaystyle \frac{k_B T}{e}\) |
出典:令和5年度第一種電気主任技術者理論科目B問題問6
解説
読解で解ける問題ではあるので時間があれば選択してもいいと思います。私的にはこの年は問7の方が簡単だったと思います。
温度差\(\Delta T\)が生じることによって電位差\(\Delta V\)が発生する現象
単なる知識の問題です。異なる金属または半導体に温度差\(\Delta T\)が生じることによって電位差\(\Delta V\)が発生する現象をゼーベック効果といいます。
ペルチエ効果:異なる金属を接合し電圧をかけ電流を流すと、接合点で熱の吸収・放出が起こる現象
トムソン効果:一つの金属上で温度の差がある2点間に電流を流すと、熱を吸収したり発生したりする現象
半導体内の電界\(E\)
電界\(E\)は
\( \displaystyle E = - \frac{\Delta V}{L} \)
で表されます。解答候補に次元が電界になる選択肢がこれしかないため容易に解けるかと思います。
\(\displaystyle \frac{dp}{dx} \)の式
両端子が開放されている場合、①式と②式で表される電流密度の総和は0となると問題にあるように、以下が成り立ちます。
\begin{aligned} \displaystyle -eD_h \frac{dp}{dx} + ep\mu_h E &= 0 \\ \frac{dp}{dx} &= \frac{p\mu_h E}{D_h} \end{aligned}
ここに、\(\displaystyle D_h = \frac{k_BT}{e}\mu_h\)と\( \displaystyle E = - \frac{\Delta V}{L} \)を代入します。
\begin{aligned} \frac{dp}{dx} &= - \frac{p\mu_h \Delta V}{L D_h} \\ &= - \frac{p\mu_h \Delta V}{L \left( \frac{k_BT}{e}\mu_h \right)} \\ &= - \frac{ep \Delta V}{L k_BT}\\ &=- \frac{e }{k_BT} \frac{\Delta V}{L}p\\ \end{aligned}
よって答えは(ト)です。
\(\displaystyle \frac{\Delta V}{\Delta T}\)の式
問題文にある
\(\displaystyle \frac{dp}{dx} = - \frac{dp}{dT} \frac{\Delta T}{L} \)
に、(3)の答えである\(\displaystyle \frac{dp}{dx} =- \frac{e }{k_BT} \frac{\Delta V}{L}p \)を代入します。
\begin{aligned} \displaystyle - \frac{e }{k_BT} \frac{\Delta V}{L}p &= - \frac{dp}{dT} \frac{\Delta T}{L} \\ \frac{\Delta V}{\Delta T} &= \frac{k_B T}{e} \frac{1}{p} \frac{dp}{dT} \\ \end{aligned}
よって答えは(ヨ)です。
正孔濃度\(p\)が与えられた時の\(\displaystyle \frac{\Delta V}{\Delta T}\)
\( p = UT^{\frac{3}{2}} \exp\left(-\dfrac{eV_F}{k_B T}\right) \)を\(T\)で微分します。
積の微分公式\(\dfrac{d}{dx} \{f(x) g(x)\} = \dfrac{df(x)}{dx} g(x) + f(x) \dfrac{dg(x)}{dx} \)を用います。
\begin{aligned} \frac{dp}{dT} &= \left(\frac{3}{2} U T^{\frac{1}{2}}\right) \exp\left(-\frac{eV_F}{k_B T}\right) + \left(UT^{\frac{3}{2}}\right) \left\{\exp\left(-\frac{eV_F}{k_B T}\right) \cdot \frac{eV_F}{k_B T^2}\right\} \\ &= \frac{3}{2} U T^{\frac{1}{2}} \exp\left(-\frac{eV_F}{k_B T}\right) + \frac{U eV_F T^{\frac{3}{2}}}{k_B T^2} \exp\left(-\frac{eV_F}{k_B T}\right) \\ &= \frac{3}{2} U T^{\frac{1}{2}} \exp\left(-\frac{eV_F}{k_B T}\right) + \frac{U eV_F}{k_B T^{\frac{1}{2}}} \exp\left(-\frac{eV_F}{k_B T}\right) \\ &= U T^{\frac{1}{2}} \exp\left(-\frac{eV_F}{k_B T}\right) \left( \frac{3}{2} + \frac{eV_F}{k_B T} \right) \\ \end{aligned}
これと\(p\)を\( \dfrac{\Delta V}{\Delta T} = \dfrac{k_B T}{e} \dfrac{1}{p} \dfrac{dp}{dT} \)に代入します。
\begin{aligned} \dfrac{\Delta V}{\Delta T} &= \dfrac{k_B T}{e} \dfrac{1}{p} \dfrac{dp}{dT} \\ &= \frac{k_B T}{e} \cdot \frac{1}{UT^{\frac{3}{2}} \exp\left(-\frac{eV_F}{k_B T}\right)} \cdot \left\{ U T^{\frac{1}{2}} \exp\left(-\frac{eV_F}{k_B T}\right) \left( \frac{3}{2} + \frac{eV_F}{k_B T} \right) \right\} \\ &= \frac{k_B T}{e} \cdot \frac{T^{\frac{1}{2}}}{T^{\frac{3}{2}}} \cdot \left( \frac{3}{2} + \frac{eV_F}{k_B T} \right) \\ &= \frac{k_B}{e} \left( \frac{3}{2} + \frac{eV_F}{k_B T} \right) \\ &= \frac{3}{2} \frac{k_B}{e} + \frac{V_F}{T} \\ \end{aligned}
よって答えは(ホ)です。
分母が3にならないことが分かれば途中からの計算は不要で答えを出せます。
- (1)ヘ ゼーベック
- (2)ヲ \(\displaystyle \frac{\Delta V}{L}\)
- (3)ト \(\displaystyle \frac{e}{k_B T} \frac{\Delta V}{L}\)
- (4)ヨ \(\displaystyle \frac{k_B T}{e}\)
- (5)ホ \(\displaystyle \frac{3}{2} \frac{k_B}{e}\)