電験一種 R5年 理論 問5
次の文章は、三相交流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
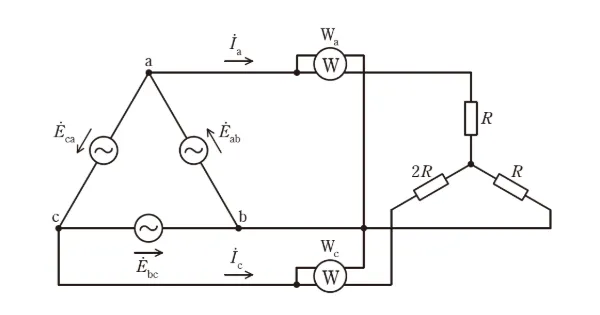
図のように、対称三相交流電源が、\(R [\Omega]\) 及び \(2R [\Omega]\) の抵抗で構成された Y 形負荷に接続されている。線間電圧は \(|\dot{E}_{ab}| = |\dot{E}_{bc}| = |\dot{E}_{ca}| = E [V]\) であり、\(\dot{E}_{ab}\) を基準フェーザとすれば、\(\dot{E}_{ab} = E\), \(\dot{E}_{bc} = Ee^{j\frac{4}{3}\pi}\), \(\dot{E}_{ca} = Ee^{j\frac{2}{3}\pi}\) で表される。
一般に、\(n\) 相の多相交流回路の消費電力は、\((n-1)\) 個の単相電力計を用いて測定できる。これは (1) の定理と呼ばれる。\(W_a\) 及び \(W_c\) は、この定理に基づいて三相交流回路の消費電力を求める単相電力計で、内部損失や誤差が無い理想的なものである。なお、\(W_a\) は電流 \(\dot{I}_a\) が矢印の向きに流れたときに、\(W_c\) は電流 \(\dot{I}_c\) が矢印の向きに流れたときに正を指示するように接続されている。
まず、\(\dot{I}_a\) の実効値 \(|\dot{I}_a|\) を求めると (2) [A] が得られる。また、\(W_a\) の指示値は、\(\dot{E}_{ab}\) に \(\dot{I}_a\) の共役複素数を乗じた複素電力の実部を求めることで得られ、(3) [W] となる。
同様に、\(\dot{I}_c\) の実効値 \(|\dot{I}_c|\) 及び \(W_c\) の指示値は、それぞれ、(4) [A] 及び (5) [W] となる。
以上から、図の三相交流回路で消費する電力は、(1) の定理より、(3) + (5) [W] となる。
| (イ)(2) | \(\displaystyle \frac{\sqrt{7}E}{5R}\) | (ロ)(3) | \(\displaystyle \frac{E^{2}}{2R}\) | (ハ) | \(\displaystyle \frac{\sqrt{7}E^{2}}{5R}\) |
| (ニ) | \(\displaystyle -\frac{E^{2}}{2R}\) | (ホ)(1) | ブロンデル | (ヘ) | \(\displaystyle \frac{3E^{2}}{2R}\) |
| (ト)(5) | \(\displaystyle \frac{3E^{2}}{10R}\) | (チ) | \(\displaystyle \frac{\sqrt{7}E}{2R}\) | (リ) | \(\displaystyle \frac{\sqrt{3}E}{2R}\) |
| (ヌ) | \(\displaystyle \frac{3E}{10R}\) | (ル)(4) | \(\displaystyle \frac{\sqrt{3}E}{5R}\) | (ヲ) | \(\displaystyle \frac{\sqrt{3}E^{2}}{5R}\) |
| (ワ) | ノートン | (カ) | \(\displaystyle \frac{E}{2R}\) | (ヨ) | テブナン |
出典:令和5年度第一種電気主任技術者理論科目B問題問5
解説
二次試験においてもこの手の計算は出てくるため、きちんとやっておくべき問題でしょう。ブロンデルの定理自体は暗記でも大丈夫です。式さえ立てられれば難しい問題ではないです。
定理の名前
n線式の多相交流回路において、その全消費電力を測定するには、少なくとも(n-1)個の単相電力計が必要であるという定理をブロンデルの定理といいます。
\( \dot{I}_a \)の実効値\( |\dot{I}_a| \)
問題の図にはありませんが、b相の線電流を\( \dot{I}_b \)とします。
下図のように一周する回路を考えます。
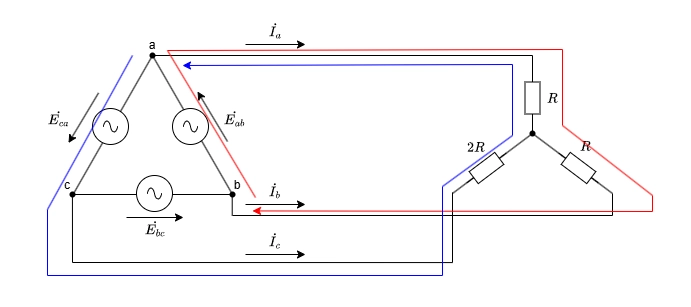
以下の関係式が成り立つので、これから\( \dot{I}_a \)を求めます。
\begin{aligned} \dot{E}_{ab} &= R\dot{I}_a - R\dot{I}_b \\ \dot{E}_{ca} &= 2R\dot{I}_c - R\dot{I}_a \\ 0 &= \dot{I}_a + \dot{I}_b + \dot{I}_c \implies \dot{I}_b = -\dot{I}_a - \dot{I}_c \\ \end{aligned}
\( \dot{I}_b \)を消去して\( \dot{I}_c \)を求めます。
\begin{aligned} \dot{E}_{ab} &= R\dot{I}_a - R(-\dot{I}_a - \dot{I}_c) \\ \dot{E}_{ab} &= 2R\dot{I}_a + R\dot{I}_c \\ \dot{I}_{c} &= \frac{\dot{E}_{ab} - 2R\dot{I}_{a}}{R} \end{aligned}
\( \dot{I}_c \)を消去して\( \dot{I}_a \)を求めます。
\begin{aligned} \dot{E}_{ca} &= 2R \left( \frac{\dot{E}_{ab} - 2R\dot{I}_a}{R} \right) - R\dot{I}_a \\ \dot{E}_{ca} &= 2\dot{E}_{ab} - 5R\dot{I}_a\\ \dot{I}_a &= \frac{2\dot{E}_{ab} - \dot{E}_{ca}}{5R}\\ \dot{I}_a &= \frac{2E - E(-\frac{1}{2} + j\frac{\sqrt{3}}{2})}{5R} \\ \dot{I}_a &= \frac{\frac{5}{2}E - j\frac{\sqrt{3}}{2}E}{5R}\\ \dot{I}_{a} &= \frac{E}{10R} (5 - j\sqrt{3})\\ \end{aligned}
絶対値を求めます。
\begin{aligned} |\dot{I}_{a}| &= \frac{E}{10R} \sqrt{5^2 + (-\sqrt{3})^2} \\ &= \frac{E}{10R} \sqrt{28} \\ \ &= \frac{\sqrt{7}E}{5R} \end{aligned}
\( W_a \)の指示値
問題文にある通り、\(W_a\)は\( \dot{E_{ab}} \)に\( \dot{I_a} \)の共役複素数を乗じた複素電力の実部なので
\begin{aligned} \displaystyle W_a &= \text{Re} \{ \dot{E}_{ab} \overline{\dot{I}_a} \} =\text{Re} \left\{ \frac{E^2}{10R} (5 + j\sqrt{3}) \right\} \\ &= \text{Re} \left\{ \frac{E^2}{2R} + j\frac{\sqrt{3}E^2}{10R} \right\} \\ &= \frac{E^2}{2R} \end{aligned}
となります。
\( \dot{I}_c \)の実効値\( |\dot{I}_c| \)
(1)より\( \dot{I}_a \)は分かっているため、\( \dot{I}_c \)の式に\( \displaystyle \dot{I}_{a} = \frac{E}{10R} (5 - j\sqrt{3}) = \frac{E}{2R} - j\frac{\sqrt{3}E}{10R}\)を代入します。
\begin{aligned} \dot{I}_c &= \frac{\dot{E}_{ab}}{R} - 2\dot{I}_a \\ &= \frac{E}{R} - 2 \left( \frac{E}{2R} - j\frac{\sqrt{3}E}{10R} \right) \\ &= j\frac{\sqrt{3}E}{5R} \\ \end{aligned}
よって、実効値は
\begin{aligned} |\dot{I}_c| &= \frac{\sqrt{3}E}{5R} \\ \end{aligned}
となります。
\( W_c \)の指示値
(2)と考え方は同様ですが、ここで気を付けなければいけないのは\(\dot{E}_{cb}\)を見てるということです。
\(\dot{E}_{cb}\)は\(\dot{E}_{bc}\)の反対なので
\begin{aligned} \dot{E}_{cb} &= -\dot{E}_{bc} = -E e^{j\frac{4}{3}\pi} = -E \left\{ \cos(\frac{4\pi}{3}) + j\sin(\frac{4\pi}{3})\right\} \\ \dot{E}_{cb} &= -E (-\frac{1}{2} - j\frac{\sqrt{3}}{2}) = E (\frac{1}{2} + j\frac{\sqrt{3}}{2}) \end{aligned}
となります。これに(4)で求めた\(\dot{I}_c\)の共役を乗じますと
\begin{aligned} W_c &= \text{Re} \{ \dot{E}_{cb} \overline{\dot{I}_c} \} \\ W_c &= \text{Re} \left\{ E \left( \frac{1}{2} + j\frac{\sqrt{3}}{2} \right) \left( -j\frac{\sqrt{3}E}{5R} \right) \right\} \\ W_c &= \text{Re} \left\{ \frac{3E^2}{10R} - j\frac{\sqrt{3}E^2}{10R} \right\} \\ W_c &= \frac{3E^2}{10R} \\ \end{aligned}
となります。
なお、三相交流回路で消費する電力は
\begin{aligned} W_a + W_c &= \frac{E^2}{2R} +\frac{3E^2}{10R} \\ &= \frac{4E^2}{5R} \\ \end{aligned}
です。
参考:\(W_a + W_c\)が三相交流回路で消費する電力になることについて
回路の合計消費電力は、各抵抗と電流より計算すると\( P = R |\dot{I}_a|^2 + R |\dot{I}_b|^2 + 2R |\dot{I}_c|^2 \)です。
一方、\(W_a + W_c\)は
\begin{aligned} W_a + W_c = \text{Re} \{ \dot{E}_{ab} \overline{\dot{I}_a} + \dot{E}_{cb} \overline{\dot{I}_c} \} \\ \end{aligned}
で表せます。ここに、\(\dot{E}_{ab} =R\dot{I}_a - R\dot{I}_b \)、\(\dot{E}_{cb} = 2R\dot{I}_c - R\dot{I}_b \)を代入します。
なお、以後の計算で\(A \bar{A} = |A|^2\)です。
\begin{aligned} W_a + W_c &= \text{Re} \{ (R\dot{I}_a - R\dot{I}_b) \overline{\dot{I}_a} + (2R\dot{I}_c - R\dot{I}_b) \overline{\dot{I}_c} \} \\ &= R |\dot{I}_a|^2 + 2R |\dot{I}_c|^2 - \text{Re} \{R \dot{I}_b (\overline{\dot{I}_a} + \overline{\dot{I}_c}) \} \end{aligned}
ここで、\( \overline{\dot{I}_a} + \overline{\dot{I}_c} = -\overline{\dot{I}_b}\)であることを考慮すると
\begin{aligned} W_a + W_c &= R |\dot{I}_a|^2 + 2R |\dot{I}_c|^2 - \text{Re} \{R \dot{I}_b (-\overline{\dot{I}_b}) \} \\ &= R |\dot{I}_a|^2 + R |\dot{I}_b|^2 + 2R |\dot{I}_c|^2 \end{aligned}
となり、三相交流回路の消費電力と一致しました。
- (1)ホ ブロンデル
- (2)イ \(\displaystyle \frac{\sqrt{7}E}{5R}\)
- (3)ロ \(\displaystyle \frac{E^{2}}{2R}\)
- (4)ル \(\displaystyle \frac{\sqrt{3}E}{5R}\)
- (5)ト \(\displaystyle \frac{3E^{2}}{10R}\)