電験一種 R5年 理論 問4
次の文章は、電気回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
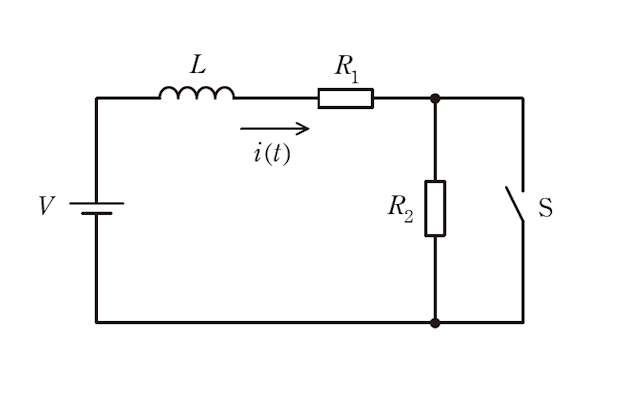
図の回路において、時刻 \(t<0\) ではスイッチ S は開いており、回路は定常状態にある。この回路において、図に示すように回路の電流を \(i(t)\) とし、\(t=0\) でスイッチ S を閉じるものとすると、\(t\ge0\) においては次式の回路方程式が成り立つ。
\(\displaystyle L \frac{di(t)}{dt} + R_1 i(t) = V\) ①
スイッチ S を閉じた直後の回路の電流を \(i(0)\) とし、①式の両辺をラプラス変換すれば、次式を得る。ただし、\(i(t)\) のラプラス変換を \(I(s)\) と表記する。
(1)\(\displaystyle = \frac{V}{s}\)
ここで、\(i(0) = \)(2) であることから、ラプラス変換された回路方程式である②式より、次式を得る。
\(I(s) = \)(3)\(\displaystyle + \frac{L}{sL + R_1} \cdot \frac{V}{R_1 + R_2}\)
③式の両辺を逆ラプラス変換すれば、\(t\geqq0\) における \(i(t)\) は、次式となる。
\(i(t) = \)(4)\(\displaystyle + \frac{V}{R_1 + R_2} e^{-\frac{t}{\tau}}\)
ただし、時定数 \(\tau = \)(5) である。
| (イ) | \(\displaystyle \frac{V}{L}\) | (ロ) | \(\displaystyle \frac{V}{R_2}\left(1 - e^{-\frac{t}{\tau}}\right)\) | (ハ)(4) | \(\displaystyle \frac{V}{R_1}\left(1 - e^{-\frac{t}{\tau}}\right)\) |
| (ニ)(5) | \(\displaystyle \frac{L}{R_1}\) | (ホ) | \(\displaystyle \frac{V}{R_1 + R_2}\left(1 - e^{-\frac{t}{\tau}}\right)\) | (ヘ) | \(\displaystyle \frac{L}{R_1 + R_2}\) |
| (ト)(2) | \(\displaystyle \frac{V}{R_1 + R_2}\) | (チ) | \(\displaystyle \frac{R_1}{L}\) | (リ) | \(L[sI(s) - I(s)] + R_1 i(0)\) |
| (ヌ) | \(\displaystyle \frac{V}{R_1}\) | (ル) | \(\displaystyle \frac{V}{s(sL + R_2)}\) | (ヲ) | \(L[sI(s) + i(0)] + R_1 I(s)\) |
| (ワ) | \(\displaystyle \frac{V}{s(sL + R_1 + R_2)}\) | (カ)(3) | \(\displaystyle \frac{V}{s(sL + R_1)}\) | (ヨ)(1) | \(L[sI(s) - i(0)] + R_1 I(s)\) |
出典:令和5年度第一種電気主任技術者理論科目A問題問4
解説
ラプラス変換での回路方程式の解き方を学べる問題です。
ラプラス変換した回路方程式
ラプラス変換の公式\(\displaystyle \mathcal{L}\left\{ \frac{df(t)}{dt} \right\} = sF(s) - f(0) \)より
\(\displaystyle L [sI(s) - i(0)] + R_1 I(s) = \frac{V}{s}\)
です。
電流の初期値\(i(0)\)
定常状態においてリアクトル\(L\)は短絡とみなせ、\(R_1\)と\(R_2\)だけの回路になるため、\(i(0)\)は
\(\displaystyle i(0) = \frac{V}{R_1 + R_2}\)
となります。
ラプラス変換された電流\(I(s)\)
(1)に\(\displaystyle i(0) = \frac{V}{R_1 + R_2}\)を代入し整理します。
\begin{aligned} L [sI(s) - i(0)] + R_1 I(s) &= \frac{V}{s} \\ L \left[ sI(s) - \frac{V}{R_1 + R_2} \right] + R_1 I(s) &= \frac{V}{s}\\ sLI(s) - \frac{LV}{R_1 + R_2} + R_1 I(s) &= \frac{V}{s} \\ (sL + R_1) I(s) &= \frac{V}{s} + \frac{LV}{R_1 + R_2}\\ I(s) = \frac{V}{s(sL + R_1)} + &\frac{L}{sL + R_1} \cdot \frac{V}{R_1 + R_2} \end{aligned}
となります。
よって答えは\(\displaystyle \frac{V}{s(sL + R_1)} \)です。
逆ラプラス変換した\(i(t)\)
下の式を逆ラプラス変換します。
\begin{aligned} I(s) = \frac{V}{s(sL + R_1)} + \frac{LV}{(R_1 + R_2)(sL + R_1)} \\ \end{aligned}
右辺第二項はそのまま逆ラプラス変換できます。第一項は部分分数分解する必要があります。
第一項について考えます。
\begin{aligned} \frac{V}{s(sL + R_1)} &= \frac{V}{L s (s + \displaystyle \frac{R_1}{L})} = \frac{A}{s} + \frac{B}{s +\displaystyle \frac{R_1}{L}} \\ \frac{V}{L} &= A (s + \frac{R_1}{L}) + B s\\ \end{aligned}
この時
\begin{aligned} (A+B) s &= 0 \\ A= \frac{V}{R_1} \\ \end{aligned}
が成り立ちますので、\(\displaystyle B = - \frac{V}{R_1}\)となります。
よって、第一項の逆ラプラス変換は
\begin{aligned} \frac{V}{s(sL + R_1)} &= \frac{V}{R_1} \left( \frac{1}{s} - \frac{1}{s + \dfrac{R_1}{L}} \right)\\ \mathcal{L}^{-1}\left\{ \frac{V}{s(sL + R_1)} \right\} &= \frac{V}{R_1} (1 - e^{-\frac{R_1}{L} t})\\ \end{aligned}
となります。
第二項も逆ラプラス変換をし、これらを足し合わせた\(i(t) \)は以下となります。なお、ここで\(\displaystyle \tau = \frac{L}{R_1}\)です。
\begin{aligned} i(t) = \frac{V}{R_1} (1 - e^{-\frac{t}{\tau}}) + \frac{V}{R_1 + R_2} e^{-\frac{t}{\tau}} \end{aligned}
よって(4)は\(\displaystyle \frac{V}{R_1} (1 - e^{-\frac{t}{\tau}})\)です。
なお、スイッチSを閉じた場合最終的に\(\displaystyle i(\infty) = \frac{V}{R_1}\)にならないといけないので、その時点で答えは(ハ)に絞れます。
時定数\(\tau\)
(4)の通り、\(\displaystyle \tau = \frac{L}{R_1}\)です。
- (1)ヨ \(L[sI(s) - i(0)] + R_1 I(s)\)
- (2)ト \(\displaystyle \frac{V}{R_1 + R_2}\)
- (3)カ \(\displaystyle \frac{V}{s(sL + R_1)}\)
- (4)ハ \(\displaystyle \frac{V}{R_1}\left(1 - e^{-\frac{t}{\tau}}\right)\)
- (5)ニ \(\displaystyle \frac{L}{R_1}\)