電験一種 R5年 理論 問3
次の文章は、直流回路の等価回路に関する記述である。文中の (0) に当てはまる最も適切なものを解答群の中から選べ。
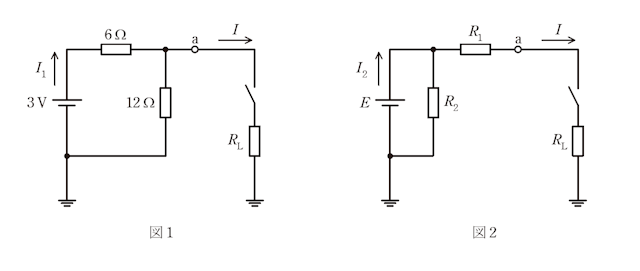
図1に示す直流電圧源と抵抗とスイッチからなる回路を考える。図2は、図1の等価回路である。
図1と図2の回路のスイッチを開いたとき、端子aの電位は等しいので電源電圧 \(E = \)(1)となる。端子aと大地間の抵抗も等しいので抵抗 \(R_1 = \)(2)となる。回路の消費電力が等しいので抵抗 \(R_2 = \)(3)となる。
次に、図1と図2の回路のスイッチを閉じて回路に同じ負荷抵抗 \(R_L\) を接続すると、\(R_L\) を流れる電流 \(I\) は同じ値となる。このとき、図1の直流電圧源を流れる電流 \(I_1\) と、図 2 の直流電圧源を流れる電流 \(I_2\) を求めると、\(I_1 = \)(4), \(I_2 = \)(5)となる。\(I_1\) と \(I_2\) の値から、負荷抵抗 \(R_L\) が同じなら図1と図2の回路が消費する電力は等しいことが分かる。
| (イ)(4) | \(\displaystyle \frac{1}{6} \times \frac{12 + R_L}{4 + R_L} [A]\) | (ロ) | \(\displaystyle \frac{7}{4} \times \frac{6 + R_L}{4 + R_L} [A]\) | (ハ) | \(\displaystyle \frac{5}{2} \times \frac{8 + R_L}{4 + R_L} [A]\) |
| (ニ) | \(\displaystyle \frac{5}{3} \times \frac{8 + R_L}{4 + R_L} [A]\) | (ホ) | \(\displaystyle \frac{7}{6} \times \frac{6 + R_L}{4 + R_L} [A]\) | (ヘ)(5) | \(\displaystyle \frac{1}{4} \times \frac{12 + R_L}{4 + R_L} [A]\) |
| (ト) | \(7\Omega\) | (チ)(1) | \(2V\) | (リ) | \(5\Omega\) |
| (ヌ) | \(9\Omega\) | (ル) | \(6V\) | (ヲ) | \(3\Omega\) |
| (ワ) | \(12V\) | (カ)(2) | \(4\Omega\) | (ヨ)(3) | \(8\Omega\) |
出典:令和5年度第一種電気主任技術者理論科目A問題問3
解説
簡単な問題ですが、このような問題は他の受験者も正答率が高いため落とせない問題です。
電源電圧\(E\)
図1の端子aの電圧\(V_{a1}\)を求めます。
\(\displaystyle V_{a1} = 3 \times \frac{12 }{6 + 12 } = 2 \)
図2においても端子aの電圧は等しくならないといけません。スイッチSが開いているとき、端子aには電流は流れませんので端子aの電圧\(=E\)となります。よって\(E=2\text{[V]}\)です。
抵抗\(R_1\)
図1において端子aから電源側を見た抵抗\(R_{a1}\)を計算します。
\(\displaystyle R_{a1} = \frac{6 \times 12 }{6 + 12} = 4 \)
図2において、端子aから電圧源を短絡して見た電源側の抵抗は\(R_1\)です。よって\(R_1=R_{a1}\)となり、\(R_1=4\text{[Ω]}\)となります。
抵抗\(R_2\)
図1の消費電力\(P_1\)を求めます。
\(\displaystyle P_1 = \frac{3^2}{6+12} = 0.5 \text{[W]}\)
図2のスイッチを開いている時の消費電力\(P_2\)は、\(R_1\)には電流が流れないので
\(\displaystyle P_2 = \frac{E^2}{R_2} \)
となります。これより\(R_2\)を求めると
\begin{aligned} \displaystyle 0.5 &= \frac{2^2}{R_2}\\ \displaystyle R_2 &= \frac{2^2}{0.5}\\ \displaystyle R_2 &= 8\text{[Ω]} \end{aligned}
となります。
図1の直流電圧源を流れる電流\(I_1\)
テブナンの定理より電流\(I\)を求めます。
\begin{aligned} \displaystyle I &= \frac{2}{4+R_L}\\ \end{aligned}
\(12 \text{[Ω]}\)の抵抗に流れる電流を\(I_{1b}\)とすると
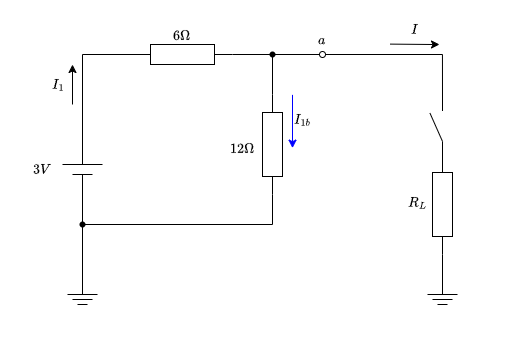
\begin{aligned} \displaystyle I_{1b} &= \frac{2R_L}{12(4+R_L)}\\ \end{aligned}
\(I_1\)は\(I\)と\(I_{1b}\)の和なので
\begin{aligned} \displaystyle I_1 &= I + I_{1b} \\ &= \frac{2}{4+R_L} + \frac{2R_L}{12(4+R_L)}\\ &= \frac{24}{12(4+R_L)} + \frac{2R_L}{12(4+R_L)}\\ &= \frac{24+2R}{12(4+R_L)} \\ &= \frac{1}{6} \times \frac{12 + R_L}{4 + R_L} \\ \end{aligned}
図2の直流電圧源を流れる電流\(I_2\)
電流\(I\)は(4)と等しいです。抵抗\(R_2\)には、\(E=2\text{[V]}\)がそのままかかりますので、その電流を\(I_{2b}\)とすると
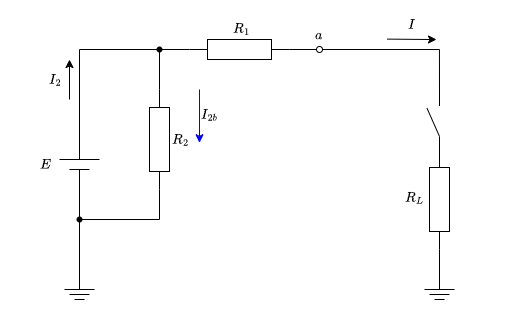
\begin{aligned} \displaystyle I_{2b} &= \frac{E}{R_2}\\ &= \frac{2}{8}\\ &=\frac{1}{4} \end{aligned}
\(I_2\)は\(I\)と\(I_{2b}\)の和なので
\begin{aligned} \displaystyle I_2 &= I + I_{2b} \\ &= \frac{2}{4+R_L} + \frac{1}{4}\\ &= \frac{8}{4(4+R_L)} + \frac{4+R_L}{4(4+R_L)}\\ &= \displaystyle \frac{1}{4} \times \frac{12 + R_L}{4 + R_L}\\ \end{aligned}
- (1)チ \(2V\)
- (2)カ \(4\Omega\)
- (3)ヨ \(8\Omega\)
- (4)イ \(\displaystyle \frac{1}{6} \times \frac{12 + R_L}{4 + R_L} [A]\)
- (5)ヘ \(\displaystyle \frac{1}{4} \times \frac{12 + R_L}{4 + R_L} [A]\)