電験一種 R4年 理論 問6
次の文章は、真空中において交流電界から力を受けた電子の運動に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
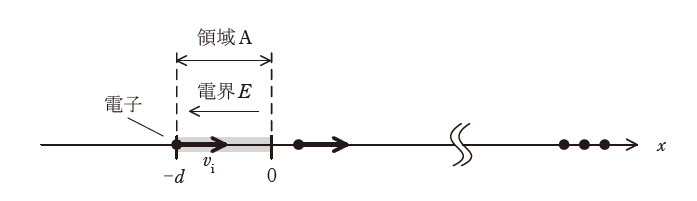
真空中で図のように、位置\(x = -d\) の電子源から電子が初速度\(v_i\)で一定の時間間隔 \(\Delta t\) ごとに\(x\)軸の正方向に次々と放出されている状況を考える。\(n\)番目に放出される電子の放出時刻を\(t = n \Delta t\)と定義する。ただし、\(n = 0, 1, 2, \cdots \) である。また、電子間に働くクーロン反発などの相互作用は無視し、電子の質量は一定とする。
領域\(A \left(-d \leqq x \leqq 0\right) \) には、\(x\)軸の負方向に \(E = E_0 \sin(\omega t)\) の電界が印加されており、電子の電荷を\( -e (e \gt 0) \)とすると、電子は電界から力を受けて運動する。電子の質量を\(m\)とすると、運動の第2法則より電子の速度\(v\)に関して、次の方程式が成り立つ。
\(\dfrac{dv}{dt} = \)(1)\(\sin(\omega t)\) …①
電子が領域 A を通過する時間が十分短いとみなせる場合、電子が領域 A の右端 (\(x = 0\)) に到達した際の速度 \(v_{x0}\) は、通過時間 \(\delta t\) を用いて次のように表される。
\(v_{x0} = v_i + \dfrac{dv}{dt} \delta t\) …②
したがって、\(n\)番目に放出された電子の \(x = 0\) における速度 \(v_n\) は、①式に \(t = n \Delta t\) を代入して左辺の \(\dfrac{dv}{dt}\) を②式に代入すると、次の式で表される。ただし、\(\delta t = \dfrac{d}{v_i}\) と仮定する。
\(v_n = v_i + \)(2)\( \sin(\omega n \Delta t)\) …③
\(n\)番目に放出された電子は\(x \gt 0\) の領域では速度 \(v_n\) で等速直線運動するので、時刻\(t\)における電子の位置 \(x_n\) は、次のように表される。なお、通過時間 \(\delta t\) は無視する。
\(x_n = v_n (t - n \Delta t)\) …④
③式の \(\omega n \Delta t\) が十分小さい場合には、sin 関数は次のように近似できる。
\(\sin(\omega n \Delta t) \approx \omega n \Delta t\) …⑤
遅れ時間 \(n\Delta t\) に比例した大きさの電界で加速されるため、後から出発した電子が先に出発した電子に追いつくことができる。追いつく位置を求めよう。
③式に⑤式を適用して④式に代入し、\(\Delta t\) の2乗の項を無視すると次式を得る。
\(x_n \approx v_i t + ( \)(3)\( ) n \Delta t\) …⑥
⑥式に、(3)\( = 0 \)となる条件を課すと、ある時刻 \(t = \)(4) において、\(x_n \)が\(n\)に依存しないことが導かれる。このことは、⑤式を満たす複数の\(n\)の電子群が、同じ時刻に、同一の位置に集群することを意味する。この集群位置は、
\(x_n \approx \)(5)である。このようにして電子流に密度の濃淡が形成される。この現象は、高周波発振や増幅などの機能を有する電子管等に応用されている。
| (イ) | \(\displaystyle \frac{eE_0 d}{mv_i} - \omega t\) | (ロ) | \(\displaystyle \frac{eE_0 d}{v_i}\) | (ハ) | \(\displaystyle \frac{eE_0 v_i}{md} \omega t - v_i\) |
| (ニ) | \(\displaystyle \frac{E_0}{em}\) | (ホ)(2) | \(\displaystyle \frac{eE_0 d}{mv_i}\) | (ヘ)(4) | \(\displaystyle \frac{mv_i^2}{eE_0 d \omega}\) |
| (ト) | \(\displaystyle \frac{md}{eE_0 \omega}\) | (チ)(1) | \(\displaystyle \frac{eE_0}{m}\) | (リ) | \(eE_0\) |
| (ヌ) | \(\displaystyle \frac{eE_0 v_i}{md}\) | (ル)(5) | \(\displaystyle \frac{mv_i^3}{eE_0 d \omega}\) | (ヲ) | \(\displaystyle \frac{mv_i^2 d}{eE_0 \omega}\) |
| (ワ) | \(\displaystyle \frac{mv_i}{eE_0 d \omega}\) | (カ)(3) | \(\displaystyle \frac{eE_0 d}{mv_i} \omega t - v_i\) | (ヨ) | \(\displaystyle \frac{mv_i}{eE_0 d \omega^2}\) |
出典:令和4年度第一種電気主任技術者理論科目B問題問6
解説
誘導に従って解く問題なので内容的には難しくありませんが、本番は時間の余裕がないため過去問を繰り返して慣れることが重要かと思います。
電子の速度\(v\)に関して成り立つ方程式
電子が受ける力\(F\)は\(F= eE\)で表されます。この問題では\(E = E_0 \sin(\omega t)\) なので、\(F(t) = eE_0 \sin(\omega t)\)となります。
また、運動方程式は\(F = ma\)で表されます。ここで\(m\)は物体の質量、\(a\)は物体の加速度です。
加速度\(a\)は速度\(v\)の時間微分であり、\(a= \dfrac{dv}{dt}\)です。したがって、運動方程式は\(F = m \dfrac{dv}{dt}\)となります。
これらの\(F\)は等しいので、ここから\(\dfrac{dv}{dt}\)を求めます。
\begin{aligned} m \frac{dv}{dt} &= eE_0 \sin(\omega t) \\ \frac{dv}{dt} &= \frac{eE_0}{m} \sin(\omega t) \\ \end{aligned}
よって答えは(チ)の\(\dfrac{eE_0}{m}\)です。
\(n\)番目に放出された電子の\(x = 0\)における速度\(v_n\)
(1)の式に\(t= n \Delta t\)を代入すると\(\displaystyle \frac{dv}{dt} = \frac{eE_0}{m} \sin(\omega n \Delta t)\)となります。
誘導に従いこれを与えられた式に代入すると
\begin{aligned} v_n = v_i + \frac{eE_0}{m} \sin(\omega n \Delta t) \cdot \delta t\\ \end{aligned}
となります。\(\delta t = \dfrac{d}{v_i}\)なので、これを代入すると
\begin{aligned} v_n &= v_i + \frac{eE_0}{m} \sin(\omega n \Delta t) \cdot \frac{d}{v_i}\\ &= v_i + \frac{eE_0 d}{m v_i} \sin(\omega n \Delta t)\\ \end{aligned}
となります。よって答えは(ホ)の\(\dfrac{eE_0 d}{m v_i}\)です。
\(\Delta t\)の2乗の項を無視して得られる式
sin関数の近似式\(\sin(\omega n \Delta t) \approx \omega n \Delta t\)を用いて(2)を近似すると
\begin{aligned} v_n &= v_i + \frac{eE_0 d}{m v_i} \sin(\omega n \Delta t) \\ &\approx v_i + \frac{eE_0 d}{m v_i} \cdot \omega n \Delta t \\ \end{aligned}
となるので、これを\(x_n = v_n (t - n \Delta t)\)に代入します。
\begin{aligned} x_n &= v_n (t - n \Delta t) \\ &\approx \left( v_i + \frac{eE_0 d}{m v_i} \cdot \omega n \Delta t \right) (t - n \Delta t) \\ \end{aligned}
これを展開すると
\begin{aligned} &\left( v_i + \frac{eE_0 d}{m v_i} \omega n \Delta t \right) (t - n \Delta t) \\ = &v_i (t - n \Delta t) + \left( \frac{eE_0 d}{m v_i} \omega n \Delta t \right) (t - n \Delta t) \\ = &v_i t - v_i n \Delta t + \frac{eE_0 d \omega n \Delta t}{m v_i} t - \frac{eE_0 d \omega n (\Delta t)^2}{m v_i} \\ = &v_i t + \frac{eE_0 d \omega n \Delta t}{m v_i} t - v_i n \Delta t - \frac{eE_0 d \omega n (\Delta t)^2}{m v_i} \\ \end{aligned}
となりますが、\(\Delta t\)の2乗の項は無視するので
\begin{aligned} &v_i t + \frac{eE_0 d \omega n \Delta t}{m v_i} t - v_i n \Delta t \\ = &v_i t + \left( \frac{eE_0 d}{m v_i} \omega t - v_i \right) n \Delta t \\ \end{aligned}
よって答えは(カ)の\(\displaystyle \frac{eE_0 d}{mv_i} \omega t - v_i\)となります。
\(x_n \)が\(n\)に依存しない時刻\(t\)
(3)の答え\(\displaystyle \frac{eE_0 d}{mv_i} \omega t - v_i\)が0になる時の\(t\)を求めればいいので、
\begin{aligned} \frac{eE_0 d}{m v_i} \omega t - v_i &= 0\\ \frac{eE_0 d}{m v_i} \omega t &= v_i \\ t &= \frac{m v_i^2}{eE_0 d \omega}\\ \end{aligned}
よって答えは(ヘ)の\(\displaystyle \frac{mv_i^2}{eE_0 d \omega}\)です。
集群位置
(4)の時、\(x_n \approx v_i t\)なので、ここに(4)で求めた\(t\)を代入すると
\begin{aligned} x_n &\approx v_i t\\ &\approx \frac{mv_i^3}{eE_0 d \omega}\\ \end{aligned}
よって答えは(ル)の\(\displaystyle \frac{mv_i^3}{eE_0 d \omega}\)です。
- (1)チ \(\displaystyle \frac{eE_0}{m}\)
- (2)ホ \(\displaystyle \frac{eE_0 d}{mv_i}\)
- (3)カ \(\displaystyle \frac{eE_0 d}{mv_i} \omega t - v_i\)
- (4)ヘ \(\displaystyle \frac{mv_i^2}{eE_0 d \omega}\)
- (5)ル \(\displaystyle \frac{mv_i^3}{eE_0 d \omega}\)