電験一種 R4年 理論 問5
問5 次の文章は、RC回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
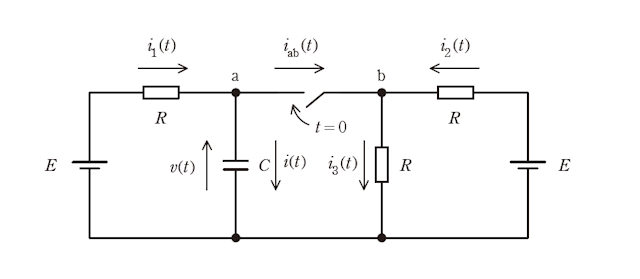
図のように、一次側と二次側に直流電圧源 \(E\) が接続された抵抗 \(R\) と静電容量 \(C\), スイッチからなる回路を考える。時刻 \(t<0\) ではスイッチは開いており、回路は定常状態にあるものとする。時刻 \(t=0\) でスイッチを閉じた。
節点 a と節点 b において、キルヒホッフの電流則を適用すると、\(t\geqq0\) で静電容量 \(C\) を流れる電流 \(i(t)\) と三つの抵抗 \(R\) をそれぞれ流れる電流 \(i_1(t)\), \(i_2(t)\), \(i_3(t)\) との関係は、
\(i(t) = i_1(t) + \)(1)············································ ①
となる。①式の左辺に静電容量 \(C\) の電圧 \(v(t)\) と電流 \(i(t)\) の関係式 \(\displaystyle i(t) = C \frac{dv(t)}{dt}\) を代入し、右辺を \(v(t)\) と \(E\) の式に書き直すと、
\(\displaystyle C \frac{dv(t)}{dt} = \)(2)············································ ②
を得る。回路の初期条件から \(v(t)\) の初期値 \(v(0)\) を決定すると、②式の解は、
\(v(t) = \)(3)············································ ③
となる。
このとき、節点 a と節点 b の電位に注意すると、直流電圧源 \(E\) から流れる電流 \(i_1(t)\) と \(i_2(t)\) は、\(t=0\) では (4) であり、①式より静電容量 \(C\) の電流 \(i(t)\) は, \(t=0\) では \(i(0) = \)(5) となることが分かる。
| (イ)(4) | \(i_1(0) = i_2(0) = 0\) | (ロ) | \(\displaystyle -\frac{3}{R}v(t) + \frac{3E}{R}\) | (ハ)(3) | \(\displaystyle Ee^{-\frac{3}{CR}t} + \frac{2E}{3}\left(1 - e^{-\frac{3}{CR}t}\right)\) |
| (ニ) | \(i_1(0) = i_2(0) = \displaystyle \frac{E}{3R}\) | (ホ)(5) | \(\displaystyle -\frac{E}{R}\) | (ヘ) | \(\displaystyle \frac{E}{3}e^{-\frac{3}{CR}t} + E\left(1 - e^{-\frac{3}{CR}t}\right)\) |
| (ト) | \(i_3(t) - i_2(t)\) | (チ) | \(i_2(t) + i_3(t)\) | (リ) | \(\displaystyle \frac{E}{2}e^{-\frac{3}{CR}t} + \frac{E}{3}\left(1 - e^{-\frac{3}{CR}t}\right)\) |
| (ヌ) | \(\displaystyle \frac{E}{3R}\) | (ル) | \(\displaystyle -\frac{3}{R}v(t) + \frac{E}{R}\) | (ヲ)(2) | \(\displaystyle -\frac{3}{R}v(t) + \frac{2E}{R}\) |
| (ワ) | \(\displaystyle \frac{2E}{3R}\) | (カ)(1) | \(i_2(t) - i_3(t)\) | (ヨ) | \(i_1(0) = 0 \text{ かつ } i_2(0) = \displaystyle \frac{E}{2R}\) |
出典:令和4年度第一種電気主任技術者理論科目B問題問5
解説
A問題の過渡現象よりは難しいですが、それでも過渡現象は計算パターンが決まっているので点を取りたいところです。
\(t\geqq0\) で静電容量 \(C\) を流れる電流 \(i(t)\)
下図のように、静電容量\(C\)には\(i_1(t)\)と\(i_2(t)-i_3(t)\)が流れ込みますので
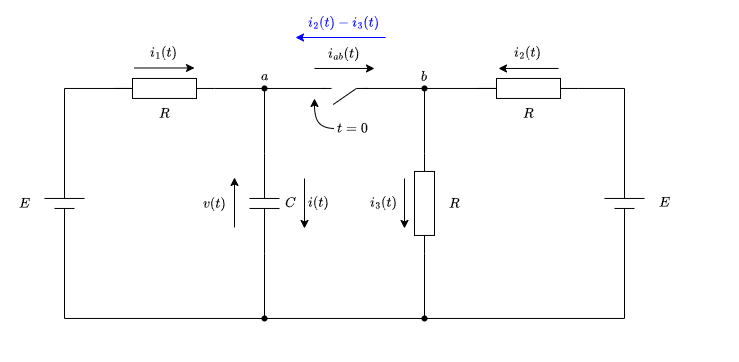
\(\displaystyle i(t)= i_1(t) + i_2(t) - i_3(t)\)
となります。
右辺を\(v(t)\)と\(E\)の式に書き直す
下図の各赤、緑、青の閉回路について考えます。
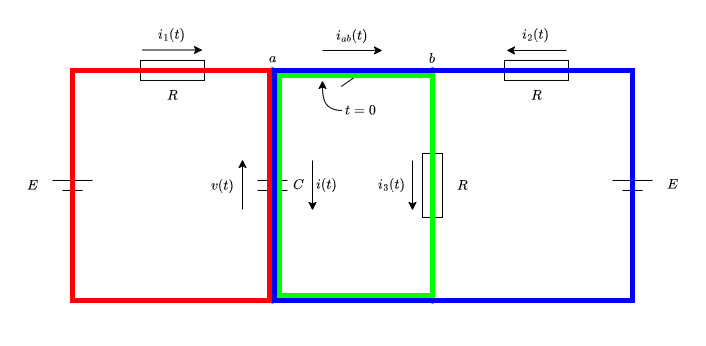
赤の閉回路
\(E = R i_1(t) + v(t) \)
緑の閉回路
\(v(t) = R i_3(t) \)
青の閉回路
\(E = R i_2(t) + v(t) \)
上式より、\(i_1(t)\)、\(i_2(t)\)、\(i_3(t)\)を求めます。
\begin{aligned} i_1(t) &= \frac{E - v(t)}{R}\\ i_2(t) &= \frac{E - v(t)}{R} \\ i_3(t) &= \frac{v(t)}{R} \\ \end{aligned}
これを\(\displaystyle C \frac{dv(t)}{dt} = i_1(t) + i_2(t) - i_3(t)\)に代入します。
\begin{aligned} \displaystyle C \frac{dv(t)}{dt} &= \frac{E - v(t)}{R} + \frac{E - v(t)}{R} - \frac{v(t)}{R} \\ &= -\frac{3}{R} v(t) + \frac{2E}{R}\\ \end{aligned}
よって答えは\(\displaystyle -\frac{3}{R} v(t) + \frac{2E}{R}\)です。
\( v(t) \)を求める
微分方程式\(\displaystyle C \frac{dv(t)}{dt} = -\frac{3}{R} v(t) + \frac{2E}{R}\)を解きます。
スイッチを閉じる前は静電容量\(C\)は\(E\)で充電されていますので、\(v(0)=E\)です。
まずは\(E=0\)として過渡解\(v_h(t)\)を求めます。
\begin{aligned} C \frac{dv_h(t)}{dt} &= -\frac{3}{R} v_h(t) \\ \frac{dv_h(t)}{v_h(t)} &= -\frac{3}{CR} dt \\ \int \frac{dv_h(t)}{v_h(t)} &= \int -\frac{3}{CR} dt \\ \ln|v_h(t)| &= -\frac{3}{CR} t + K \quad Kは積分定数\\ v_h(t) &= e^{-\frac{3}{CR} t + K} = A e^{-\frac{3}{CR} t} \quad A=e^Kは任意の定数 \\ \end{aligned}
次に定常解\(v_p(t)\)を求めます。
\(\displaystyle \frac{dv(t)}{dt}=0\)として
\begin{aligned} 0 &= -\frac{3}{R}v_p(t) + \frac{2E}{R} \\ v_p(t) &= \frac{2E}{3} \end{aligned}
となります。
一般解は、
\begin{aligned} v(t) &= v_h(t) + v_p(t) \\ &= A e^{-\frac{3}{CR} t} + \frac{2E}{3}\\ \end{aligned}
となります。\(v(0)\)を利用して\(A\)を求めます。
\begin{aligned} E &= A e^{-\frac{3}{CR} (0)} + \frac{2E}{3} \\ E &=A e^{0} + \frac{2E}{3} \\ E &= A + \frac{2E}{3} \\ A &= E - \frac{2E}{3} = \frac{E}{3} \end{aligned}
よって
\begin{aligned} v(t) &= \frac{E}{3} e^{-\frac{3}{CR} t} + \frac{2E}{3} \\ &= \frac{E}{3} e^{-\frac{3}{CR} t} + \frac{2E}{3} (1 - e^{-\frac{3}{CR} t}) + \frac{2E}{3} e^{-\frac{3}{CR} t} \\ &= E e^{-\frac{3}{CR} t} + \frac{2E}{3} (1 - e^{-\frac{3}{CR} t}) \\ \end{aligned}
となります。
なお、\(t=0\)の時\(E\)になるのは(ハ)だけなので、それで答えを選ぶ方が時間的にいいかと思います。
\(i_1(t)\)と\(i_2(t)\)の\(t=0\)での電流値
(2)で\(i_1(t)\)と\(i_2(t)\)の式を求めています。
\begin{aligned} i_1(t) &= \frac{E - v(t)}{R}\\ i_2(t) &= \frac{E - v(t)}{R} \\ \end{aligned}
ここで、\(v(0)=E\)なので、\( i_1(0) = i_2(0) = 0 \)となることが分かります。
静電容量\(C\)の電流\(i(0)\)
(1)で\(i(t)\)の式を求めています。
\(\displaystyle i(t)= i_1(t) + i_2(t) - i_3(t)\)
\( i_1(0) = i_2(0) = 0 \)なので、
\(\displaystyle i(0)= - i_3(0)\)
となります。
\(\displaystyle i_3(t) = \frac{v(t)}{R} \)
であり、\(v(0)=E\)なので、
\(\displaystyle i_3(0) = \frac{E}{R} \)
となるので、
\(\displaystyle i(0)= -\frac{E}{R} \)
となります。
微分を用いても同様の答えが得られます。
\begin{aligned} i(t) &= C\frac{dv(t)}{dt} = -\frac{3E}{R} e^{-\frac{3}{CR} t} + \frac{2E}{R} e^{-\frac{3}{CR} t} = -\frac{E}{R} e^{-\frac{3}{CR} t}\\ i(0) &= -\frac{E}{R} e^{-\frac{3}{CR} (0)} \\ &= -\frac{E}{R} \end{aligned}
- (1)カ \(\displaystyle i_2(t) - i_3(t)\)
- (2)ヲ \(\displaystyle -\frac{3}{R}v(t) + \frac{2E}{R}\)
- (3)ハ \(\displaystyle Ee^{-\frac{3}{CR}t} + \frac{2E}{3}\left(1 - e^{-\frac{3}{CR}t}\right)\)
- (4)イ \(\displaystyle i_1(0) = i_2(0) = 0\)
- (5)ホ \(\displaystyle -\frac{E}{R}\)