電験一種 R4年 理論 問4
次の文章は、三相交流回路に関する記述である。文中の (1) に当てはまる最も適切なものを解答群の中から選べ。
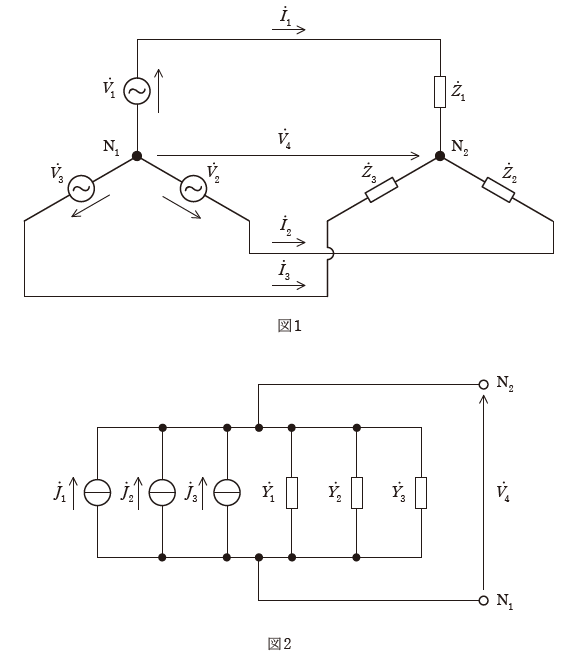
図1の回路は、不平衡三相電源に不平衡三相負荷が接続されたY結線不平衡三相回路である。
ミルマンの定理より、図1の回路は交流電流源\(\dot{J}_1\),\(\dot{J}_2\), \(\dot{J}_3\) 及び三相負荷のアドミタンス \(\displaystyle \dot{Y}_1 = \frac{1}{\dot{Z}_1}\), \(\displaystyle \dot{Y}_2 = \frac{1}{\dot{Z}_2}\), \(\displaystyle \dot{Y}_3 = \frac{1}{\dot{Z}_3}\) を用いて、図2に示す等価回路に変換できる。ただし、図2の等価回路において、交流電流源\(\dot{J}_m = \)(1),\(m = 1, 2, 3\)である。
図1の中性点 N₁ - N₂ 間の電圧を\(\dot{V}_4\)とすれば、図1の各相の線電流 \(\dot{I}_m = \)(2), \(m = 1, 2, 3\) となる。また、図2の等価回路から電圧\(\dot{V}_4 = \)(3)となる。ただし、電圧 \(\dot{V}_4\)は図1及び図2の向きを正とする。
図1において、電源電圧を平衡三相である\(\dot{V}_1 = 100 V\), \(\dot{V}_2 = 100e^{-j\frac{2}{3}\pi} [V]\), \(\dot{V}_3 = 100e^{-j\frac{4}{3}\pi} [V]\) とし、三相負荷のインピーダンス \(\dot{Z}_1 = j [\Omega]\), \(\dot{Z}_2 = 1 \Omega\), \(\dot{Z}_3 = 1 \Omega\) とする。このとき、中性点 N₁ - N₂ 間の電圧 \(\dot{V}_4 = \)(4)\([V]\) となる。なお、\(\dot{V}_2 + \dot{V}_3 = \)(5)となることに注意せよ。
| (イ) | \(\displaystyle -\frac{100 + j100}{2 + j}\) | (ロ)(1) | \(\dot{Y}_m \dot{V}_m\) | (ハ)(2) | \((\dot{V}_m - \dot{V}_4)\dot{Y}_m\) |
| (ニ) | \(\dot{V}_1 + \dot{V}_2 + \dot{V}_3\) | (ホ) | \(\sqrt{\dot{Y}_m \dot{V}_m}\) | (ヘ)(5) | \(-\dot{V}_1\) |
| (ト)(3) | \(\displaystyle \frac{\dot{Y}_1\dot{V}_1 + \dot{Y}_2\dot{V}_2 + \dot{Y}_3\dot{V}_3}{\dot{Y}_1 + \dot{Y}_2 + \dot{Y}_3}\) | (チ) | \(\displaystyle -\frac{100 - j100}{2 - j}\) | (リ) | \(\dot{V}_1\) |
| (ヌ) | \((\dot{V}_1 + \dot{V}_2 + \dot{V}_3)\dot{Y}_m\) | (ル) | \(0\) | (ヲ) | \((\dot{V}_m + \dot{V}_4)\dot{Y}_m\) |
| (ワ)(4) | \(\displaystyle -\frac{100 + j100}{2 - j}\) | (カ) | \(\displaystyle \frac{\dot{Y}_m \dot{V}_m}{2}\) | (ヨ) | \(\displaystyle \frac{\dot{Y}_1 + \dot{Y}_2 + \dot{Y}_3}{\dot{Y}_1\dot{V}_1 + \dot{Y}_2\dot{V}_2 + \dot{Y}_3\dot{V}_3}\) |
出典:令和4年度第一種電気主任技術者理論科目A問題問4
解説
ミルマンの定理を覚えていれば問題ないですが、覚えていなくても解けはする問題です。
交流電流源\(\dot{J}_m \)
電圧源と電流源の等価変換より
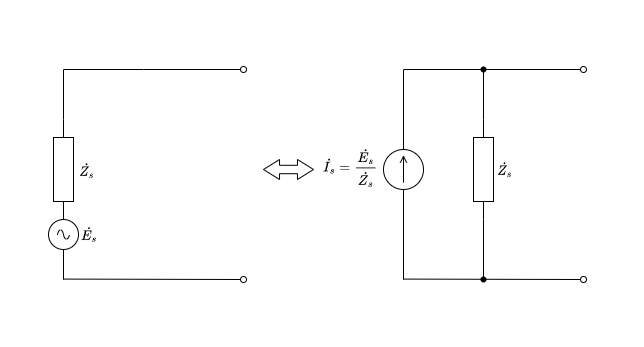
\( \dot{J}_m = \dfrac{\dot{V}_m}{\dot{Z}_m} = \dot{Y}_m \dot{V}_m \)
となります。
各相の線電流 \(\dot{I}_m \)
中性点の電圧が\(\dot{V}_4\)なので、キルヒホッフの第ニ法則より
\( \dot{I}_m = (\dot{V}_m - \dot{V}_4) \dot{Y}_m \)
となります。
電圧\(\dot{V}_4 \)
ミルマンの定理
\( \displaystyle V_0 = \frac{\displaystyle \sum_{i=1}^{N} Y_i V_i}{\displaystyle \sum_{i=1}^{N} Y_i} \)
より、\(\displaystyle \dot{V}_4 = \frac{\dot{Y}_1\dot{V}_1 + \dot{Y}_2\dot{V}_2 + \dot{Y}_3\dot{V}_3}{\dot{Y}_1 + \dot{Y}_2 + \dot{Y}_3}\)となります。
なお、この問題の解答候補は(ト)、(ヌ)、(ヨ)になると思いますが、このうち次元が電圧になるのは(ト)だけなのでそれでも正解を出せます。
不平衡三相負荷の電圧\(\dot{V}_4 \)
\begin{aligned} \dot{Y}_1 &= \dfrac{1}{\dot{Z}_1} = \dfrac{1}{j} = -j \text{[S]} \\ \dot{Y}_2 &= 1 \text{[S]} \\ \dot{Y}_3 &= 1 \text{[S]} \\ \end{aligned}
これを(3)の解答に代入します。
\begin{aligned} \frac{\dot{Y}_1 \dot{V}_1 + \dot{Y}_2 \dot{V}_2 + \dot{Y}_3 \dot{V}_3}{\dot{Y}_1 + \dot{Y}_2 + \dot{Y}_3} &= \frac{(-j) \dot{V}_1 + (1) \dot{V}_2 + (1) \dot{V}_3}{ (-j) + 1 + 1 } \\ &= \frac{-j \dot{V}_1 + \dot{V}_2 + \dot{V}_3}{2 - j} \\ \end{aligned}
ここで、(5)の答えとなる\(\dot{V}_2 + \dot{V}_3\)を求めます。
\begin{aligned} \dot{V}_2 + \dot{V}_3 &= 100 e^{-j \frac{2}{3}\pi} + 100 e^{-j \frac{4}{3}\pi} \\ &= 100 \left\{ \cos(-\frac{2}{3}\pi) + j\sin(-\frac{2}{3}\pi) \right\} + 100 \left\{ \cos(-\frac{4}{3}\pi) + j\sin(-\frac{4}{3}\pi) \right\} \\ &= 100 \left( -\frac{1}{2} - j\frac{\sqrt{3}}{2} \right) + 100 \left( -\frac{1}{2} + j\frac{\sqrt{3}}{2} \right) \\ &= -100 \\ &= - \dot{V}_1 \\ \end{aligned}
ベクトルオペレータ\(a\)の式\( 1+a+a^2=0\)より、\(\dot{V}_1 + \dot{V}_2 + \dot{V}_3 = 0\)なので、そこが分かっていれば計算は不要かと思います。
先ほどの式を\(\dot{V}_2 + \dot{V}_3 = - \dot{V}_1\)を使用して整理します。
\begin{aligned} \frac{-j \dot{V}_1 + \dot{V}_2 + \dot{V}_3}{2 - j} &= \frac{-j \dot{V}_1 + (-\dot{V}_1)}{2 - j}\\ &= -\frac{(1 + j) \dot{V}_1}{2 - j}\\ &= -\frac{100 + j100 }{2 - j} \\ \end{aligned}
よって答えは(ワ)の\(\displaystyle -\frac{100 + j100 }{2 - j} \)です。
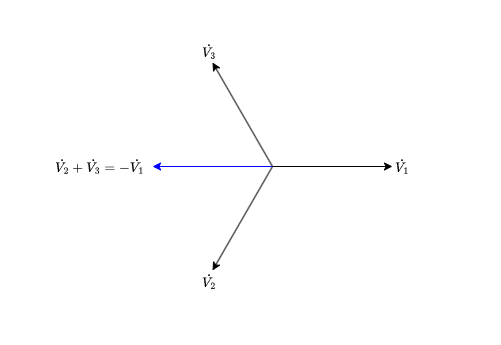
\(\dot{V}_2 + \dot{V}_3\)
(4)の通り、(ヘ)の\(- \dot{V}_1 \)です。
参考にベクトル図を載せます。
- (1)ロ \(\dot{Y}_m \dot{V}_m\)
- (2)ハ \((\dot{V}_m - \dot{V}_4)\dot{Y}_m\)
- (3)ト \(\displaystyle \frac{\dot{Y}_1\dot{V}_1 + \dot{Y}_2\dot{V}_2 + \dot{Y}_3\dot{V}_3}{\dot{Y}_1 + \dot{Y}_2 + \dot{Y}_3}\)
- (4)ワ \(\displaystyle -\frac{100 + j100}{2 - j}\)
- (5)ヘ \(-\dot{V}_1\)