電験一種 R4年 理論 問3
次の文章は、直流回路の合成抵抗に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
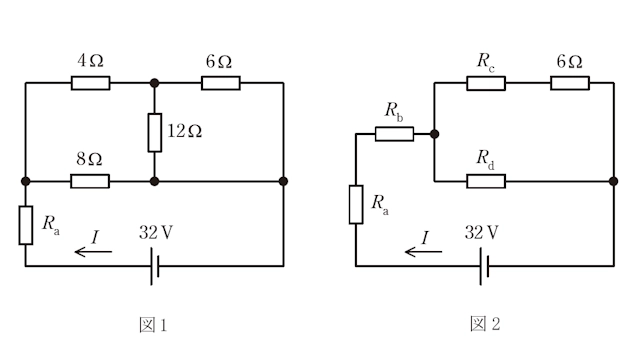
図1において、電源側から見た回路全体の合成抵抗 \(R\) を求めたい。なお、抵抗 \(R_a\) は 60W の電力を消費しており、5Ωより小さいことが分かっている。まず、抵抗 4Ω, 8Ω 及び 12Ω からなる Δ 形抵抗に対してΔ-Y変換を施し、図2の等価回路に変換すると、\(R_b = \)(1)\( \Omega\), \(R_c = \)(2)\( \Omega\), \(R_d = \)(3)\( \Omega\) が得られる。
次に、\(R\) は、回路を流れる電流 \(I\) と電源電圧から得られるので、\(I\) を求めることとする。
電流 \(I\) を求めると、\(I = \)(4)\( A \)となる。したがって、電源側から見た回路全体の合成抵抗は、\(R = \)(5)\( \Omega\) となる。
| (イ)(1) | \(\displaystyle \frac{4}{3}\) | (ロ) | \(2.4\) | (ハ)(5) | \(6.4\) |
| (ニ) | \(\displaystyle \frac{3}{4}\) | (ホ) | \(\displaystyle \frac{1}{3}\) | (ヘ)(3) | \(4\) |
| (ト) | \(\displaystyle \frac{2}{3}\) | (チ) | \(3\) | (リ) | \(8\) |
| (ヌ) | \(3.2\) | (ル)(2) | \(2\) | (ヲ) | \(10\) |
| (ワ) | \(12\) | (カ)(4) | \(5\) | (ヨ) | \(6\) |
出典:令和4年度第一種電気主任技術者理論科目A問題問3
解説
簡単な問題なのでこういう問題で確実に点を取りたいところです。
Δ-Y変換は1回導出した方が理解が深まっていいかと思います。
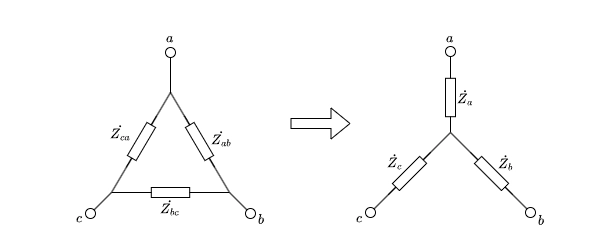
Δ-Y変換の式
\begin{aligned} \dot{Z}_a = \frac{\dot{Z}_{ca} \dot{Z}_{ab}} {\dot{Z}_{ab} + \dot{Z}_{bc} + \dot{Z}_{ca}} \\ \dot{Z}_b = \frac{\dot{Z}_{ab} \dot{Z}_{bc}}{\dot{Z}_{ab} + \dot{Z}_{bc} + \dot{Z}_{ca}} \\ \dot{Z}_c = \frac{\dot{Z}_{bc} \dot{Z}_{ca}}{\dot{Z}_{ab} + \dot{Z}_{bc} + \dot{Z}_{ca}} \\ \end{aligned}
Y-Δ変換の式(今回の問題では使用しません)
\begin{aligned} \dot{Z}_{ab} = \frac{\dot{Z}_a \dot{Z}_b + \dot{Z}_b \dot{Z}_c + \dot{Z}_c \dot{Z}_a}{\dot{Z}_c} \\ \dot{Z}_{bc} = \frac{\dot{Z}_a \dot{Z}_b + \dot{Z}_b \dot{Z}_c + \dot{Z}_c \dot{Z}_a}{\dot{Z}_a} \\ \dot{Z}_{ca} = \frac{\dot{Z}_a \dot{Z}_b + \dot{Z}_b \dot{Z}_c + \dot{Z}_c \dot{Z}_a}{\dot{Z}_b} \\ \end{aligned}
Δ-Y変換した時の抵抗\(R_b\)
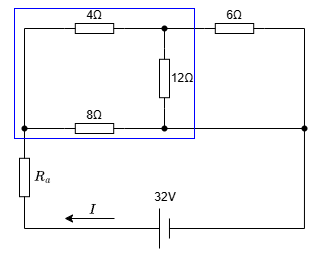
上の公式に従って、青枠の部分をΔ-Y変換します。
よって
\begin{aligned} \displaystyle R_b &= \frac{4 \times 8}{4 + 12 + 8 } \\ &= \frac{4}{3} \end{aligned}
です。
Δ-Y変換した時の抵抗\(R_c\)
同様に抵抗\(R_c\)は
\begin{aligned} \displaystyle R_c = &=\frac{4 \times 12}{4 + 12 + 8} \\ &= \frac{48 }{24 } \\ &= 2 \end{aligned}
です。
Δ-Y変換した時の抵抗\(R_d\)
同様に抵抗\(R_d\)は
\begin{aligned} \displaystyle R_d = &=\frac{8 \times 12}{4 + 12 + 8 } \\ &= \frac{96 }{24 } \\ &= 4 \end{aligned}
です。
電流\(I\)
\(R_b\)、\(R_c\)、\(R_d\)、\(6\Omega\)による合成抵抗をまず求めます。
\begin{aligned} \displaystyle R_{total} &= R_b+ \frac{(R_c + 6) \times R_d}{(R_c + 6) + R_d} \\ &=\frac{4}{3} + \frac{8 \times 4 }{8 + 4 } \\ &= \frac{4}{3} + \frac{8}{3} \\ &= 4 \end{aligned}
となります。
全体の抵抗はこれと\(R_a\)の直列であり、また\(R_a\)は60Wを消費しているとありますので、これより以下が成り立ちます。
\begin{aligned} I &= \frac{32}{R_a + R_{total}} = \frac{32}{R_a + 4}\\ 60 &= R_a I^2 \end{aligned}
\(R_a\)について整理します。
\begin{aligned} R_a &= \frac{32}{I} - 4 \quad \cdots (3) \\ \end{aligned}
これを\( 60 = R_a I^2 \)に代入し、二次方程式を解きます。
\begin{aligned} 60 &= \left( \frac{32}{I} - 4 \right) I^2 \\ 60 &= 32I - 4 I^2 \\ 4 I^2 - 32 I + 60 &= 0 \\ I^2 - 8 I + 15 & = 0 \\ (I - 3)(I - 5) &= 0 \\ \end{aligned}
\(I\)の候補となる値は3Aもしくは5Aであることが分かりました。
2つの候補となる電流値を用いて\(R_a\)を出します。
\begin{aligned} R_a = \frac{32}{3} - 4 = \frac{32 - 12}{3} = \frac{20}{3} \approx 6.67 \Omega \\ R_a = \frac{32}{5} - 4 = \frac{32 - 20}{5} = \frac{12}{5} = 2.4 \Omega \\ \end{aligned}
\(R_a\)は\(5\Omega\)より小さいので、\(R_a\)は\(2.4 \Omega \)となり、この時電流\(I\)は5Aとなります。
電源側から見た回路全体の合成抵抗
\(R_b\)、\(R_c\)、\(R_d\)、\(6\Omega\)による合成抵抗は\(4 \Omega\)であり、それと\(2.4 \Omega \)の直列であることから\(6.4 \Omega \)です。
- (1)イ \(\displaystyle \frac{4}{3}\)
- (2)ル \(2\)
- (3)ヘ \(4\)
- (4)カ \(5\)
- (5)ハ \(6.4\)