電験一種 R4年 理論 問1
次の文章は、複素数を用いて2次元の電界を解析的に求める手法に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
図1のように、\(z = x + jy\) で表される複素平面上で、\(y=0\), \(x \geqq 0\) で記述される原点が端で無限に長く細い導体に電圧が印加されているとき、等角写像法を用いて平面上の電界及び電位を解析的に求めることができる。
等角写像法では、電気力線と等電位線が既知である別の複素平面 \(w = u + jv\) を考え、\(z\) に写像する写像関数 \(z = f(w)\) を与える。 \(f(w)\) が連続で微分可能であれば、電気力線と等電位線が(1)という関係が、写像を行っても保たれる。
ここで、図2のように、複素平面 \(w\) の \(v \geqq 0\) の範囲において、\(u\)軸上に置かれた無限に長い電極は、\(f(w) = w^2\) により、\(x + jy = \left( u + jv \right)^2 \) の関係が成り立つことで、\(z\) 平面上において図1に示す電極に写像される。 \(w\) には、\(u\) 軸と平行に等電位線が、\(v\) 軸と平行に電気力線が構成されるので、それらを \(z\) 上に写像すれば \(z\) 上での等電位線と電気力線が解析的に求められることになる。
例えば、図3において \(v=1\) の式で表される等電位線は、\(z\) 上では (2) の式で表される。また、\(u=0\) 及び \(u=1\) の式で表される2本の電気力線は、\(z\) 上ではそれぞれ (3) 及び (4) の式で表される。ただし、各図において、実線の矢印は電気力線、破線は等電位線を表す。
これらのことにより、図3に描かれた電気力線と等電位線を \(z\) 上に写像すると (5) の図が得られる。
| (イ) | 1点に収束する | (ロ) | \(x = |y| - 2\) | (ハ) | \(x = -|y| + 2, y \geqq 0\) |
| (ニ)(2) | \(x = \displaystyle \frac{y^2}{4} - 1\) | (ホ)(4) | \(x = 1 - \displaystyle \frac{y^2}{4}, y \geqq 0\) | (ヘ) | \(x = - \displaystyle \frac{y^2}{4}, y \geqq 0\) |
| (ト) | \(y = 0, x \leqq -1\) | (チ) | \(x = \displaystyle \frac{y^2}{4} - 2\) | (リ)(3) | \(y = 0, x \leqq 0\) |
| (ヌ)(1) | 直交する | (ル) | \(x = -|y|\) | (ヲ) | 交わらない |
| (ワ)(5) | 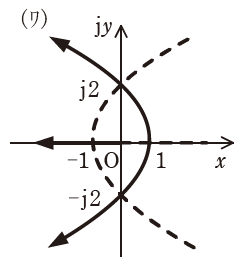 |
(カ) | 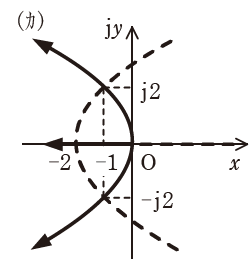 |
(ヨ) | 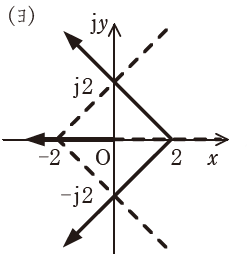 |
出典:令和4年度第一種電気主任技術者理論科目A問題問1
解説
難しい問題のように思えますが、このような問題はほとんどの場合読解で解けるようになっています。
電気力線と等電位線の関係
電気力線と等電位線は直行します。
理由は他サイトで調べてもらった方がいいと思うのでここでは省略します。
\(v=1\)の式で表される等電位線
問題文より、\(z = f(w)\)、\(f(w) = w^2\)、\(w = u + jv\)なので、
\(z = \left( u + jv \right)^2\)であることが分かります。
これに、\(v=1\)を代入すると、
\begin{aligned} z &= \left( u + jv \right)^2 \\ &= \left( u + j1 \right)^2 \\ &= u^2 -1 + j2u \\ \end{aligned}
となります。
これを、\(x + jy \)と係数比較すると\(x = u^2 -1 \)、\(y = 2u \)となることが分かります。
更に\(u\)について整理すると、\(u = \dfrac{y}{2}\)なので、これを\(x\)の式に代入します。
\begin{aligned} x &= u^2 -1 \\ &= \left(\dfrac{y}{2}\right)^2 -1 \\ &= \dfrac{y^2}{4} -1 \\ \end{aligned}
よって答えは(ニ)の\( x = \dfrac{y^2}{4} -1 \)です。
\(u=0\)の時の電気力線
(2)と同様に考えます。\(u=0\)なので、
\begin{aligned} z &= \left( u + jv \right)^2 \\ &= \left( 0 + jv \right)^2 \\ &= -v^2 \\ \end{aligned}
よって、\(x = -v^2 \)、\(y = 0 \)となります。
問題文より、\(v \geqq 0\)であり、\(v^2\)は0か正の値になることから、\(-v^2 \leqq 0\)となることが分かります。
よって答えは(リ)の\(y = 0, x \leqq 0\)です。
\(u=1\)の時の電気力線
同様に考えて
\begin{aligned} z &= \left( u + jv \right)^2 \\ &= \left( 1 + jv \right)^2 \\ &= -v^2 + 1 + j2v \\ \end{aligned}
なので、\(x = -v^2 + 1 \)、\(y = 2v \)となります。
\(v\)について整理すると、\(v = \dfrac{y}{2} \)となるので、これを\(x\)の式に代入すると
\begin{aligned} x &= -v^2 + 1 \\ &= 1 - \left(\dfrac{y}{2}\right)^2 \\ &= 1 - \dfrac{y^2}{4} \\ \end{aligned}
となります。\(v \geqq 0\)であることから、\(y \geqq 0\)となるので、
答えは(ホ)の\(x = 1 - \displaystyle \frac{y^2}{4}, y \geqq 0\)となります。
\(z\)上に写像された電気力線と等電位線
問題の図より、\(u = 1\)の時の\(x\)と\(y\)について考えます。
(4)より、\(u = 1\)のとき、\(x = 1 - \displaystyle \frac{y^2}{4}, y \geqq 0\)
\(x = 0 \)とすると、
\begin{aligned} x &= 1 - \displaystyle \frac{y^2}{4} \\ 0 &= 1 - \displaystyle \frac{y^2}{4} \\ y &= \pm 2 \\ \end{aligned}
\(y = 0 \)とすると、
\begin{aligned} x &= 1 - \displaystyle \frac{y^2}{4} \\ &= 1 - \displaystyle \frac{0^2}{4} \\ &= 1 \end{aligned}
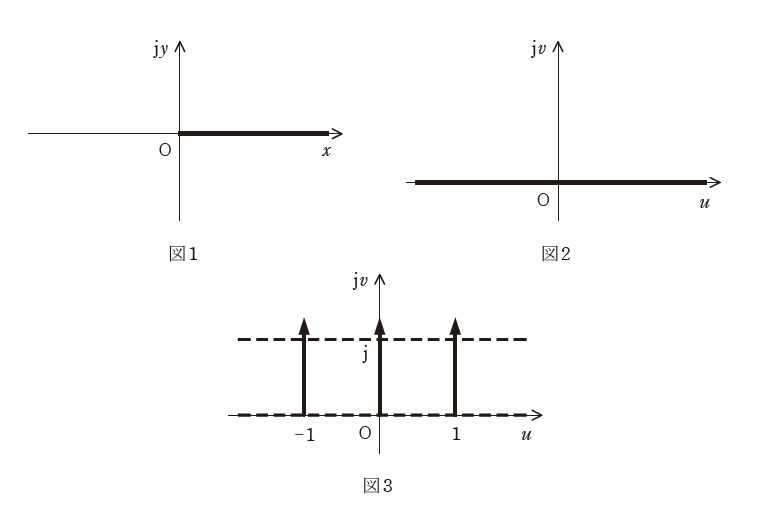
よって、\(\left(0,j2\right)\)、\(\left(0,-j2\right)\)、\(\left(1,0\right)\)を通る電気力線が存在することが分かります。
これを満たすのは(ワ)しかありません。よって答えは(ワ)となります。
- (1)ヌ 直交する
- (2)ニ \(x = \displaystyle \frac{y^2}{4} - 1\)
- (3)リ \(y = 0, x \leqq 0\)
- (4)ホ \(x = 1 - \displaystyle \frac{y^2}{4}, y \geqq 0\)
- (5)ワ
