電験一種 R3年 理論 問6
次の文章は、ホール効果測定に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
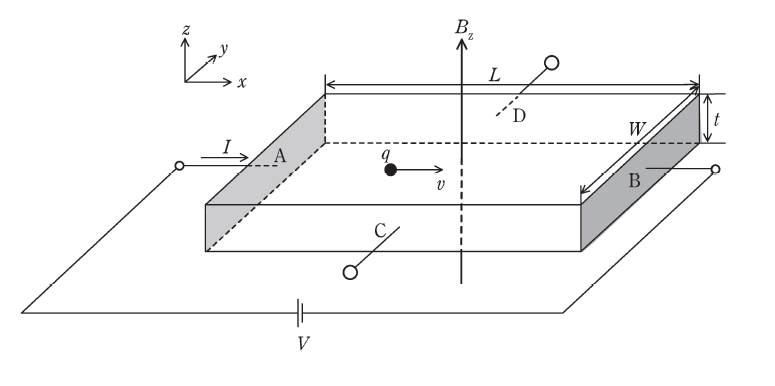
図のように、板状の半導体(長さ\(L\)、幅\(W\)、厚さ\(t\))のA面とB面の間に電圧\(V(>0)\)を印加する。半導体中のキャリアが電界から力を受けて一定速度\(v\)で運動している状況を考える。キャリアが正の電荷量\(q\)を持つ正孔の場合、正孔の濃度を\(p\)、移動度を\(\mu_h\)と仮定すると、運動の方向は\(x\)軸の正方向となり、\(v = \)(1)と表されることから、回路を流れる電流\(I\)は、\(I = \)(2)と表される。
この半導体に、図の\(z\)軸の正方向に磁束密度\(B_z(>0)\)の磁界を印加すると、正孔がローレンツ力を受けることで、C面の電位がD面に対して(3)くなる。この電位差をホール電圧\(V_H\)と定義する。定常状態では、\(V_H\)による電界から受ける力と、ローレンツ力が釣り合うことから、\(V_H = \)(4)と表される。以上の関係を用いると、\(V_H\)と\(I\)を実測することにより\(\mu_h\)とか\(p\)が得られ、\(p = \)(5)と算出される。
| (イ)(3) | 高 | (ロ) | 等し | (ハ) | \(\displaystyle \frac{\mu_h V}{W}\) | (ニ) | \(\displaystyle \frac{q p \mu_h V}{L}\) |
| (ホ) | 低 | (ヘ) | \(\displaystyle \frac{q B_z}{t} \frac{I}{V_H}\) | (ト)(1) | \(\displaystyle \frac{\mu_h V}{L}\) | (チ) | \(\displaystyle \frac{q \mu_h V B_z W}{L}\) |
| (リ)(4) | \(\displaystyle \frac{\mu_h V B_z W}{L}\) | (ヌ)(5) | \(\displaystyle \frac{B_z}{qt} \frac{I}{V_H}\) | (ル) | \(\displaystyle \frac{B_z }{qt} \frac{V_H}{I}\) | (ヲ)(2) | \(\displaystyle \frac{qp \mu_h Vt W}{L}\) |
| (ワ) | \(\displaystyle \frac{q p \mu_h V t L}{W}\) | (カ) | \(\displaystyle \frac{\mu_h L}{V}\) | (ヨ) | \(\displaystyle \frac{\mu_h V B_z W}{Lt}\) |
出典:令和3年度第一種電気主任技術者理論科目B問題問6
解説
移動度を覚えていれば比較的解きやすい問題かと思います。
半導体中のキャリアが電界から力を受けて移動する速度\(v\)
移動度と速度の関係は\( v = \mu_h E\)で表されます。ここで\(E\)は電界です。
電界は\(E = \dfrac{V}{L}\)で表されますので、
\begin{aligned} v = \mu_h \left(\dfrac{V}{L}\right)\\ \end{aligned}
となり、答えは(ト)の\(\displaystyle \frac{\mu_h V}{L}\)です。なお、移動度の単位は\( \left[ \dfrac{m^2}{V \cdot s} \right] \)です。
回路を流れる電流\( I \)
電流密度\(J\)は、単位断面積を電荷量\(q\)をもつ正孔が1秒間に\(pv\)個通過することから、
\begin{aligned} J &= qpv \\ &= qp \left(\dfrac{\mu_h V}{L} \right) \\ \end{aligned}
で表されます。
濃度の単位が\( \left[ \dfrac{1}{m^3} \right] \)なので、ここから電流密度の単位\( \left[ \dfrac{C}{m^2 \cdot s} \right] \)を導くことも可能かと思います。
図より、半導体の断面積は\(S = Wt\)であり、電流は電流密度と面積の積で表されるので
\begin{aligned} I &= JS \\ &= qp \left(\dfrac{\mu_h V}{L} \right) \times Wt \\ &= \frac{qp \mu_h Vt W}{L} \\ \end{aligned}
となり、答えは(ヲ)の\(\displaystyle \frac{qp \mu_h Vt W}{L}\)となります。
磁界が印加された時C面の電位はD面に対してどうなるか
\(z\)軸の正方向に磁界が印加されると、正孔はローレンツ力\(\mathbf{F} = q\mathbf{v} \times \mathbf{B}\)を受けます。
フレミングの左手の法則より、力の方向はC面に向かう方向です。
よって、C面に正孔が偏って分布することとなるため、C面の電位はD面に比べて高くなります。
なお、電子がキャリヤでもローレンツ力は同じ方向に働くため、その場合は正孔の場合とは逆にC面電位は低くなります。
キャリヤが正孔でも動いているのは結局電子なので力の方向が逆では?というのはよく思われている疑問のようで、正直なところ私も分かりやすい説明ができません。
ここに疑問がある場合は調べてください。問題を解くだけであればキャリヤがフレミングの左手の法則に従って力を受ける、後はそのキャリヤが正か負かで電位を判断すると割り切るのがいいと思います。
ホール電圧\(V_H\)
ホール電圧による電界は\(E_H = \dfrac{V_H}{W} \)で表されます。これによる力\(F_H\)は、
\begin{aligned} F_H &= qE_H \\ &= q \left( \dfrac{V_H}{W} \right) \\ \end{aligned}
となり、これの向きはローレンツ力と反対でD面の方に向かいます。
定常状態では、この力とローレンツ力が釣り合うので
\begin{aligned} qvB_z &= \dfrac{qV_H}{W} \\ qB_z \left(\dfrac{\mu_hV}{L}\right) &= \dfrac{qV_H}{W} \\ \dfrac{\mu_hVB_z}{L} &= \dfrac{V_H}{W} \\ V_H &= \frac{\mu_h V B_z W}{L} \\ \end{aligned}
となり、答えは(リ)の\(\displaystyle \frac{\mu_h V B_z W}{L}\)です。
正孔濃度\(p\)
(2)より、\(\displaystyle I = \frac{qp \mu_h Vt W}{L}\)です。これを\(p\)について整理すると、
\begin{aligned} p = \frac{IL}{q \mu_h Vt W} \end{aligned}
となります。また、(4)の\(V_H = \dfrac{\mu_h V B_z W}{L}\)を\(V\)について整理すると、
\begin{aligned} V &= \dfrac{V_HL}{\mu_h B_z W} \end{aligned}
上の式に下の\(V\)を代入すると
\begin{aligned} p &= \frac{IL}{q \mu_h t W} \left( \frac{\mu_h B_z W}{V_H L} \right)\\ &= \frac{B_z}{qt} \frac{I}{V_H} \end{aligned}
よって答えは(ヌ)の\(\displaystyle \frac{B_z}{qt} \frac{I}{V_H}\)です。
- (1)ト \(\displaystyle \frac{\mu_h V}{L}\)
- (2)ヲ \(\displaystyle \frac{qp \mu_h Vt W}{L}\)
- (3)イ 高
- (4)リ \(\displaystyle \frac{\mu_h V B_z W}{L}\)
- (5)ヌ \(\displaystyle \frac{B_z}{qt} \frac{I}{V_H}\)