電験一種 R3年 理論 問5
次の文章は、交流回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
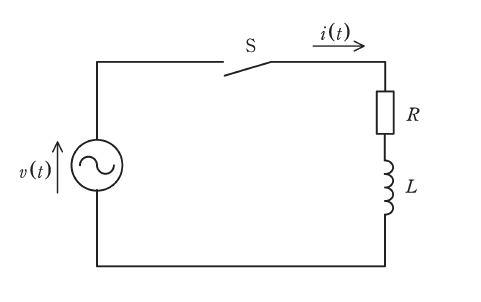
図のRL回路において、時刻\(t \lt 0\)ではスイッチSは開いている。時刻\(t = 0\)でスイッチSを閉じ、回路に正弦波交流電圧\(v(t) = V_m \sin(\omega t + \theta)\)が印加されるものとする。
回路の電流を\(i(t)\)とすれば、時刻\(t \geqq 0\)では次式の回路方程式が成立する。
(1)\( + Ri(t) = V_m \sin(\omega t + \theta)\) …①
時刻\(t \geqq 0\)における電流\(i(t)\)は、①式の定常解\(i_s(t)\)と過渡解\(i_T(t)\)の和として与えられる。
定常解\(i_s(t)\)は、正弦波交流回路の定常電流として、
\(i_s(t) = \dfrac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\omega t + \theta - \phi)\) …②
となる。ただし、\(\phi = \)(2)である。
一方、過渡解\(i_T(t)\)は、①式の右辺を0とした場合の解であるので、任意定数を\(K\)とすれば次式となる。
\(i_T(t) = K \times \)(3)
したがって、電流\(i(t)\)の一般解は、②式及び③式より、次式で与えられる。
\(i(t) = i_s(t) + i_T(t) = \dfrac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\omega t + \theta - \phi) + K \times \)(3) …④
時刻\(t = 0\)における回路の電流\(i(0) = 0\)であることに注意すれば、④式より任意定数\(K\)は次式で与えられる。
\(K = \)(4)
以上より、時刻\(t \geqq 0\)における回路の電流\(i(t)\)は、次式で与えられる。
\(i(t) = \dfrac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\omega t + \theta - \phi) + \)(4)\( \times \)(3)
なお、⑥式において\(\theta - \phi = \)(5)が成立する場合には、時刻\(t \geqq 0\)における回路の電流\(i(t)\)は定常解\(i_s(t)\)のみで表される。
| (イ) | \(\tan^{-1} \dfrac{1}{\omega LR}\) | (ロ) | \(e^{-\frac{1}{RL}t}\) | (ハ)(5) | \(0\) |
| (ニ)(2) | \(\tan^{-1} \dfrac{\omega L}{R}\) | (ホ)(3) | \(e^{-\frac{R}{L}t}\) | (ヘ) | \(\omega Li(t)\) |
| (ト) | \(\tan^{-1} \dfrac{R}{\omega L}\) | (チ) | \(\displaystyle \frac{di(t)}{dt}\) | (リ) | \(\displaystyle \frac{\pi}{4}\) |
| (ヌ)(1) | \(L \displaystyle \frac{di(t)}{dt}\) | (ル) | \(\displaystyle \frac{\pi}{2}\) | (ヲ) | \(e^{-\frac{L}{R}t}\) |
| (ワ)(4) | \(\displaystyle \frac{-V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta - \phi)\) | ||||
| (カ) | \(\displaystyle \frac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta - \phi)\) | ||||
| (ヨ) | \(\displaystyle \frac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta + \phi)\) |
出典:令和3年度第一種電気主任技術者理論科目B問題問5
解説
回路は単純ですが電源を交流にすると計算が複雑になります。とはいえ難しい問題ではないかと思います。
時刻\(t \geqq 0\)で成立する回路方程式
電験一種を受ける人にとってはサービス問題かと思います。
\begin{aligned} L\frac{ di(t)}{dt} + Ri(t) = V_m \sin(\omega t + \theta) \end{aligned}
よって答えは(ヌ)の\(L \displaystyle \frac{di(t)}{dt}\)です。
\(\sin(\omega t + \theta - \phi) \)の\( \phi \)
抵抗とインダクタンスの回路の場合電圧の位相に比べ電流の位相は遅れます。
コイルのリアクタンスが大きいほど電流の位相は遅れるので、\(\omega L\)が大きい時により\( \phi \)の値が大きくなる必要があります。
これを満たすのは(ニ)の\(\tan^{-1} \dfrac{\omega L}{R}\)です。
試験で問題を解く際は時間の関係からこの考え方で解くのが望ましいかと思いますが、未定係数法を使用して定常解\(i_s(t)\)を求めてみます。
右辺が\(\sin(\omega t + \theta)\)の形をしているため、\(i_s(t)\)が以下のような形で表されると仮定します。
\begin{aligned} i_s(t) = A \sin(\omega t + \theta) + B \cos(\omega t + \theta) \\ \end{aligned}
\(L\dfrac{ di_s(t)}{dt} + Ri_s(t) = V_m \sin(\omega t + \theta) \)の式に上の\(i_s(t)\)を代入します。
\begin{aligned} &L [A \omega \cos(\omega t + \theta) - B \omega \sin(\omega t + \theta)] + R [A \sin(\omega t + \theta) + B \cos(\omega t + \theta)] = V_m \sin(\omega t + \theta) \\ &(AR - B \omega L )\sin(\omega t + \theta) + ( A \omega L + BR)\cos(\omega t + \theta) = V_m \sin(\omega t + \theta) \\ \end{aligned}
ここで、等式が常に成り立つためには\(\sin(\omega t + \theta)\)の係数と\(\cos(\omega t + \theta )\)の係数がそれぞれ等しくなければならないので
\begin{aligned} AR - B \omega L &= V_m \\ A \omega L + BR &= 0 \\ \end{aligned}
である必要があります。
下の式より、\( B = -\dfrac{ \omega L}{R} A \)なので、これを上の式に代入すると
\begin{aligned} AR - \omega L \left( -\frac{ \omega L}{R} A \right) &= V_m \\ \left( \frac{R^2 + \omega^2 L^2}{R} \right) A &= V_m \\ A &= \frac{R V_m}{R^2 + (\omega L)^2} \\ \end{aligned}
となります。これよりBは
\begin{aligned} B = -\frac{ \omega L}{R} A = -\frac{ \omega L}{R} \cdot \frac{R V_m}{R^2 + (\omega L)^2} = -\frac{\omega L V_m}{R^2 + (\omega L)^2} \\ \end{aligned}
となります。これを定常解の式に代入すると
\begin{aligned} i_s(t) = \frac{R V_m}{R^2 + (\omega L)^2} \sin(\omega t + \theta) - \frac{\omega L V_m}{R^2 + (\omega L)^2} \cos(\omega t + \theta) \\ \end{aligned}
となります。
問題文にあるように、これを\(\sin\)関数のみにまとめます。
三角関数の合成公式を使用します。参考:三角関数の合成公式
\begin{aligned} i_s(t) &= \frac{V_m}{\sqrt{R^2 + (\omega L)^2}} \left[ \frac{R}{\sqrt{R^2 + (\omega L)^2}} \sin(\omega t + \theta) - \frac{\omega L}{\sqrt{R^2 + (\omega L)^2}} \cos(\omega t + \theta) \right] \\ &= \frac{V_m}{\sqrt{R^2 + (\omega L)^2}} [ \cos \phi \sin(\omega t + \theta) - \sin \phi \cos(\omega t + \theta) ]\\ \end{aligned}
ここで、\( \cos \phi = \dfrac{R}{\sqrt{R^2 + (\omega L)^2}} \)、\(\sin \phi = \dfrac{\omega L}{\sqrt{R^2 + (\omega L)^2}}\)です。
加法定理を用いて式を変形します。
\begin{aligned} \sin((\omega t + \theta) - \phi) = \sin(\omega t + \theta) \cos \phi - \cos(\omega t + \theta) \sin \phi \\ \end{aligned}
より、
\begin{aligned} i_s(t) = \frac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\omega t + \theta - \phi) \\ \end{aligned}
問題文に与えられた式となりました。
最後に\(\phi\)を求めます。
\begin{aligned} \tan \phi = \frac{\sin \phi}{\cos \phi} = \dfrac{\dfrac{\omega L}{\sqrt{R^2 + (\omega L)^2}}}{\dfrac{R}{\sqrt{R^2 + (\omega L)^2}}} = \frac{\omega L}{R} \\ \end{aligned}
\(\phi\)はこれの逆関数なので
\begin{aligned} \phi = \tan^{-1} \dfrac{\omega L}{R} \\ \end{aligned}
となります。
過渡解\(i_T(t)\)
\(L\dfrac{ di_T(t)}{dt} + Ri_T(t) = 0 \)の\(i_T(t)\)を求めます。
なお、試験では時定数\(\tau = \dfrac{L}{R}\)で減衰するので答えは(ホ)の\(e^{-\frac{R}{L}t}\)になる、で答えをすぐに出すべきかと思います。
変数分離します。
\begin{aligned} L \frac{di_T(t)}{dt} = -Ri_T \\ \frac{di_T(t)}{i_T(t)} = -\frac{R}{L} dt \\ \end{aligned}
両辺を積分して\(i_T(t)\)を求めます。ここで\(C\)は積分定数です。
\begin{aligned} \int \frac{1}{i_T} di_T &= \int -\frac{R}{L} dt \\ \ln |i_T(t)| &= -\frac{R}{L} t + C \\ |i_T(t)| &= e^{-\frac{R}{L} t + C} = e^{-\frac{R}{L} t} e^{C} \\ i_T(t) &= \pm e^{C} e^{-\frac{R}{L} t} \\ i_T(t) &= K e^{-\frac{R}{L} t} \quad (K = \pm e^C) \\ \end{aligned}
となり、答えを導けました。
任意定数\(K\)
一般解は定常解と過渡解の和になるので、
\begin{aligned} i(t) = i_s(t) + i_T(t) = \dfrac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\omega t + \theta - \phi) + K e^{-\frac{R}{L} t} \\ \end{aligned}
ここで、\(t=0\)のとき、\( i(t) = 0 \)なので、
\begin{aligned} 0 &= \frac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta - \phi) + K \\ K &= -\frac{V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta - \phi) \\ \end{aligned}
となり、答えは(ワ)の\(\displaystyle \frac{-V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta - \phi)\)です。
\(i(t)\)が定常解\(i_s(t)\)のみとなる条件
\(K e^{-\frac{R}{L} t} = \dfrac{-V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta - \phi) \cdot e^{-\frac{R}{L} t} = 0\)であればいいので、
\begin{aligned} \sin(\theta - \phi) = 0 \\ \theta - \phi = 0 \end{aligned}
となり、答えは(ハ)の\(0\)となります。
- (1)ヌ \(L \displaystyle \frac{di(t)}{dt}\)
- (2)ニ \(\tan^{-1} \dfrac{\omega L}{R}\)
- (3)ホ \(e^{-\frac{R}{L}t}\)
- (4)ワ \(\displaystyle \frac{-V_m}{\sqrt{R^2 + (\omega L)^2}} \sin(\theta - \phi)\)
- (5)ハ \(0\)