電験一種 R3年 理論 問4
次の文章は、三相交流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
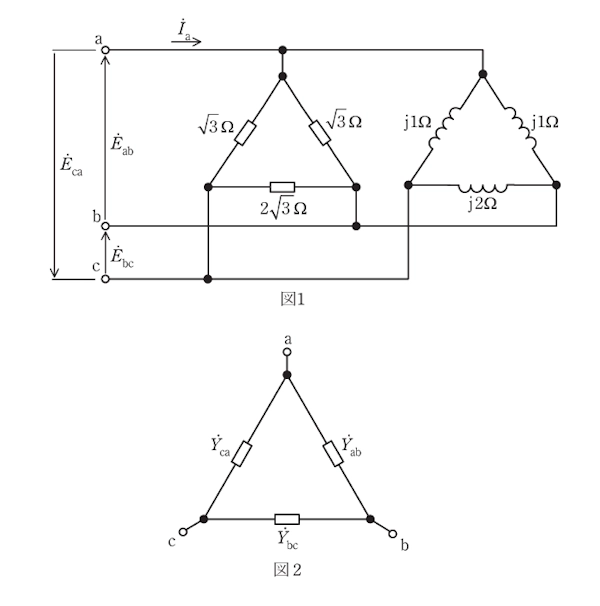
図1のように、実効値が1Vである対称三相交流電源に、二つのΔ形不平衡負荷が並列接続されている。図1の各線間電圧は\(\dot{E}_{ab}=1\angle 0^\circ\) [V] を基準に、\(\dot{E}_{bc}=a^2\dot{E}_{ab}\), \(\dot{E}_{ca}=a\dot{E}_{ab}\) とする。ただし、\(a=e^{j\frac{2}{3}\pi}\) である。
図2は、アドミタンス\(\dot{Y}_{ab}\), \(\dot{Y}_{bc}\)及び\(\dot{Y}_{ca}\)を用いて表した図1の等価回路であり、\(\dot{Y}_{ab}\)及び\(\dot{Y}_{ca}\)は(1)S, \(\dot{Y}_{bc}\)は(2)Sとなる。
線電流\(\dot{I}_a\)の実効値及び位相角を求めると、それぞれ(3)A及び(4)°となる。ただし、位相角の符号は進みを正とする。
図1で消費する有効電力は(5)Wである。
| (イ) | \(\displaystyle \frac{5\sqrt{3}}{3}\) | (ロ) | \(-45\) | (ハ)(2) | \(\displaystyle \frac{\sqrt{3}}{3} e^{-j\frac{1}{3}\pi}\) |
| (ニ) | \(2\sqrt{3}e^{-j\frac{1}{3}\pi}\) | (ホ) | \(\sqrt{3}e^{-j\frac{1}{3}\pi}\) | (ヘ) | \(\sqrt{3}\) |
| (ト) | \(\displaystyle \frac{5\sqrt{3}}{2}\) | (チ) | \(\displaystyle \frac{\sqrt{3}}{3}e^{-j\frac{2}{3}\pi}\) | (リ)(3) | \(2\) |
| (ヌ)(4) | \(-90\) | (ル) | \(\displaystyle \frac{2\sqrt{3}}{3}e^{-j\frac{2}{3}\pi}\) | (ヲ)(5) | \(\displaystyle \frac{5\sqrt{3}}{6}\) |
| (ワ) | \(-60\) | (カ) | \(2\sqrt{3}\) | (ヨ)(1) | \(\displaystyle \frac{2\sqrt{3}}{3}e^{-j\frac{1}{3}\pi}\) |
出典:令和3年度第一種電気主任技術者理論科目A問題問4
解説
比較的解きやすい問題かと思います。
アドミタンス\(\dot{Y}_{ab}\)
アドミタンス\(\dot{Y}_{ab}\)は\(\sqrt{3}\)Ωと\(j1\)Ωの並列アドミタンスなので
\begin{aligned} \displaystyle \dot{Y_{ab}} &= \frac{1}{\sqrt{3}} + \frac{1}{j1} \\ &= \frac{1}{\sqrt{3}} - j\\ &= \frac{1}{\sqrt{3}} ( 1 - j\sqrt{3} )\\ &= \frac{2}{\sqrt{3}} e^{-j\tan^{-1}\sqrt{3}}\\ &= \frac{2}{\sqrt{3}} e^{-j\frac{1}{3}\pi}\\ &= \frac{2\sqrt{3}}{3} e^{-j\frac{1}{3}\pi} \end{aligned}
です。
アドミタンス\(\dot{Y}_{bc}\)
(1)と同様にアドミタンス\(\dot{Y}_{bc}\)は\(2\sqrt{3}\)Ωと\(j2\)Ωの並列アドミタンスなので
\begin{aligned} \displaystyle \dot{Y}_{bc}&= \frac{1}{2\sqrt{3}} + \frac{1}{j2} \\ &= \frac{1}{2\sqrt{3}} - j\frac{1}{2}\\ &= \frac{1}{2\sqrt{3}} \left( 1 - j\sqrt{3} \right)\\ &= \frac{1}{\sqrt{3}} e^{-j\tan^{-1}\sqrt{3}} \\ &= \frac{1}{\sqrt{3}} e^{-j\frac{1}{3}\pi}\\ &= \frac{\sqrt{3}}{3} e^{-j\frac{1}{3}}\pi\\ \end{aligned}
です。
線電流\(\dot{I_a}\)の実効値
以下が成り立ちますので、これより\(\dot{I}_a\)を求めます。
\begin{aligned} \dot{I}_a &= \dot{I}_{ab} - \dot{I}_{ca} \\ \dot{I}_{ab} &= \dot{Y}_{ab} \dot{E}_{ab}\\ \dot{I}_{ca} &= \dot{Y}_{ca} \dot{E}_{ca}\\ \end{aligned}
まずは\(\dot{I}_{ab}\)を求めます。
\begin{aligned} \dot{I}_{ab} &= \dot{Y}_{ab} \dot{E}_{ab} = \left( \frac{2\sqrt{3}}{3} e^{-j\frac{1}{3}\pi} \right) \times 1\\ &= \frac{\sqrt{3}}{3} - j \end{aligned}
図より、\( \dot{Y}_{ca} \)は\( \dot{Y}_{ab} \)と等しいので
\begin{aligned} \dot{I}_{ca} &= \dot{Y}_{ca} \dot{E}_{ca} = \dfrac{2\sqrt{3}}{3}e^{-j\frac{1}{3}\pi } \cdot Ee^{j\frac{2}{3}\pi } \\ &= \frac{2\sqrt{3}}{3} e^{j\frac{1}{3}\pi} \\ &= \frac{2\sqrt{3}}{3} \left(\frac{1}{2} + j\frac{\sqrt{3}}{2}\right)\\ &= \frac{\sqrt{3}}{3} + j \end{aligned}
とって、\(\dot{I}_{a}\)は
\begin{aligned} \dot{I}_a &= \dot{I}_{ab} - \dot{I}_{ca} \\ &=\frac{\sqrt{3}}{3} - j - ( \frac{\sqrt{3}}{3} - j ) \\ &= -j2\\ \end{aligned}
となり、その実効値は\(2\)となります。
線電流\(\dot{I_a}\)の位相角
(3)より、\(\dot{I}_{a}\)は実部0で虚部が\(-j2\)なので位相角は\(-90 \ ° \)となります。
消費する有効電力
各抵抗には実効値1Vの電圧がかかっていますので、\( \dfrac{V^2}{R} \)より
\begin{aligned} P &= \frac{1^2}{\sqrt{3}} + \frac{1^2}{2\sqrt{3}} + \frac{1^2}{\sqrt{3}}\\ &= \frac{5}{2\sqrt{3}}\\ &= \frac{5\sqrt{3}}{6} \\ \end{aligned}
- (1)ヨ \(\displaystyle \frac{2\sqrt{3}}{3}e^{-j\frac{1}{3}\pi}\)
- (2)ハ \(\displaystyle \frac{\sqrt{3}}{3} e^{-j\frac{1}{3}\pi}\)
- (3)リ \(2\)
- (4)ヌ \(-90\)
- (5)ヲ \(\displaystyle \frac{5\sqrt{3}}{6}\)