電験一種 R3年 理論 問3
次の文章は、2端子対抵抗回路の電流、電圧に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
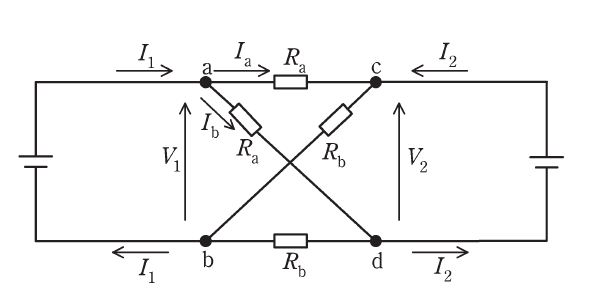
図のように2端子対抵抗回路の電流と電圧を定義する。オームの法則とキルヒホッフの法則を使って、\(\dfrac{V_1}{I_1}\) と \(\dfrac{V_2}{I_2}\) を求めてみる。
端子対a-b間の電位差\(V_1\)は、経路 a→c→b での電圧降下の和で表すと、
\(V_1 = R_a I_a + R_b \)((1)) …①
となり、経路 a→d→b での電圧降下の和で表すと、
\(V_1 = R_a I_b + R_b \)((2)) …②
となる。\(I_1 = I_a + I_b\) を利用すると、①式と②式より \(\dfrac{V_1}{I_1} = \)(3) となる。
一方、端子対c-d間の電位差\(V_2\)は経路 c→a→d での電圧降下の和で表すと、
\(V_2 = R_a (-I_a) + R_a I_b\) …③
となり、経路 c→b→d での電圧降下の和で表すと、
\(V_2 = R_b \)((1))\( + R_b \)((4)) …④
となる。③式から \(\dfrac{V_2}{R_a}\) を求め、④式から \(\dfrac{V_2}{R_b}\) を求めて加算すると、\(\dfrac{V_2}{I_2} = \)(5)となる。
| (イ) | \(R_a + R_b\) | (ロ) | \(I_b\) | (ハ) | \(I_a - I_2\) |
| (ニ) | \(R_a\) | (ホ) | \(I_b + I_2\) | (ヘ)(1) | \(I_a + I_2\) |
| (ト)(2) | \(I_b - I_2\) | (チ) | \(I_a\) | (リ) | \(-I_b\) |
| (ヌ)(4) | \(I_2 - I_b\) | (ル) | \(-I_a\) | (ヲ)(3) | \(\displaystyle \frac{1}{2}(R_a + R_b)\) |
| (ワ)(5) | \(\displaystyle \frac{2R_a R_b}{R_a + R_b}\) | (カ) | \(\displaystyle \frac{R_a R_b}{R_a + R_b}\) | (ヨ) | \(R_b\) |
出典:令和3年度第一種電気主任技術者理論科目A問題問3
解説
難しい要素はないので、理論の限られた時間で冷静に解けるかどうかだけが問題です。過去問の周回で慣れておきましょう。
経路a→c→bで表した端子対a-b間の電位差\(V_1\)
c-b間を流れる電流は図のようになりますので
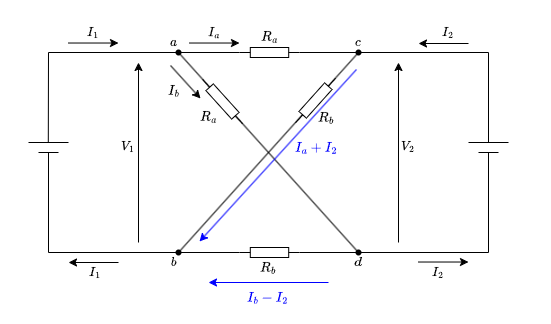
答えは(ヘ)の\(I_a + I_2\)です。
経路a→d→bで表した端子対a-b間の電位差\(V_1\)
同様に、d-b間を流れる電流は上図のようになりますので、答えは(ト)の\(I_b - I_2\)です。
①式と②式より求めた\(\dfrac{V_1}{I_1} \)
以下の3つの式を用いて\(\dfrac{V_1}{I_1} \)を求めます。
\begin{aligned} V_1 &= R_a I_a + R_b (I_a + I_2) \\ V_1 &= R_a I_b + R_b (I_b - I_2) \\ I_1 &= I_a + I_b \\ \end{aligned}
上2つの和を求め、\(I_1 = I_a + I_b\)を代入すると、
\begin{align*} V_1 + V_1 &= R_a I_a + R_b (I_a + I_2) + R_a I_b + R_b (I_b - I_2) \\ 2V_1 &= R_a I_a + R_b I_a + R_b I_2 + R_a I_b + R_b I_b - R_b I_2 \\ &= (R_a + R_b)I_a + (R_a + R_b)I_b \\ &= (R_a + R_b)(I_a + I_b) \\ &= (R_a + R_b)I_1 \\ \end{align*}
よって、
\begin{align*} 2V_1 &= (R_a + R_b)I_1 \\ \frac{V_1}{I_1} &= \frac{1}{2}(R_a + R_b) \\ \end{align*}
となるので、答えは(ヲ)の\(\displaystyle \frac{1}{2}(R_a + R_b)\)です。
経路c→b→dで表した端子対a-b間の電位差\(V_2\)
b-d間を流れる電流は図のようになりますので
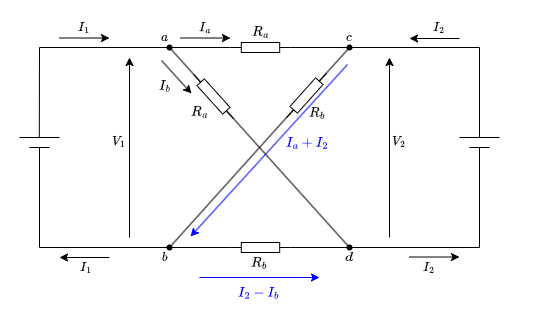
答えは(ヌ)の\(I_2 - I_b\)です。
③式と④式より求めた\(\dfrac{V_2}{I_2} \)
誘導の通り、まずは\(\dfrac{V_2}{R_a}\)を求めます。
\begin{align*} V_2 &= R_a (-I_a) + R_a I_b \\ \frac{V_2}{R_a} &= I_b - I_a \end{align*}
同様に、\(\dfrac{V_2}{R_b}\)は
\begin{align*} V_2 &= R_b (I_a + I_2) + R_b(I_2 - I_b) \\ \frac{V_2}{R_b} &= I_a + 2I_2 - I_b \end{align*}
なので、これらの和を求めると、
\begin{align*} \frac{V_2}{R_a} + \frac{V_2}{R_b} &= (I_b - I_a) + (I_a + 2I_2 - I_b) \\ V_2 \left( \frac{1}{R_a} + \frac{1}{R_b} \right) & = I_b - I_a + I_a + 2I_2 - I_b \\ V_2 \left( \frac{1}{R_a} + \frac{1}{R_b} \right) &= 2I_2 \\ \frac{V_2}{I_2} &= \frac{2}{\dfrac{1}{R_a} + \dfrac{1}{R_b}} \\ \frac{V_2}{I_2} &= \frac{2 R_a R_b}{R_a + R_b} \\ \end{align*}
よって、答えは(ワ)の\(\displaystyle \frac{2R_a R_b}{R_a + R_b}\)です。
- (1)ヘ \(I_a + I_2\)
- (2)ト \(I_b - I_2\)
- (3)ヲ \(\displaystyle \frac{1}{2}(R_a + R_b)\)
- (4)ヌ \(I_2 - I_b\)
- (5)ワ \(\displaystyle \frac{2R_a R_b}{R_a + R_b}\)