電験一種 R3年 理論 問2
次の文章は、コイルのインダクタンスに関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
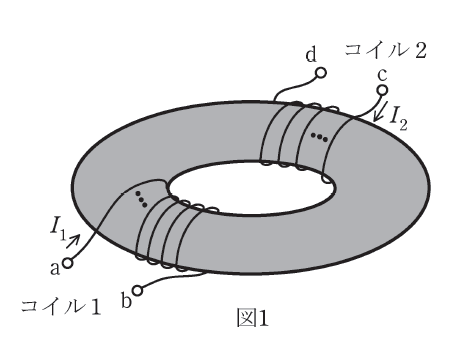
図1のように、環状鉄心にコイル1とコイル2が巻かれており、コイル1の巻数とコイル2の巻数の比は 1 : \(a\) である。各コイルに電流が流れたときには鉄心の内部にのみ磁界が発生するものとする。
コイル1の自己インダクタンスを\(L_1\)とすると、コイル2の自己インダクタンス\(L_2\)は(1)、コイル1の端子abとコイル2の端子cdの間の相互インダクタンス \(M\) は (2) と表される。図1に示す向きに\(I_1\), \(I_2\)の電流が各コイルに流れている場合には、蓄積された磁界のエネルギー\(W\)は、
\(W = \dfrac{1}{2} L_1 I_1^2 + \dfrac{1}{2} L_2 I_2^2 + M I_1 I_2\)
と表されるので、\(I_1 = -a I_2\)の場合には磁界のエネルギーは(3)となる。
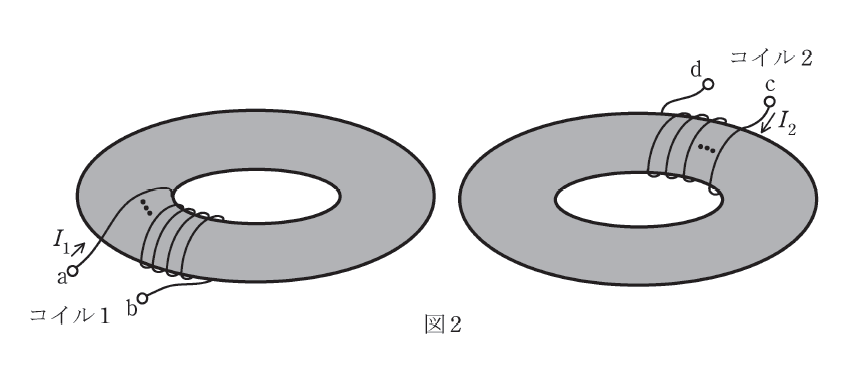
図1のコイル1の端子bとコイル2の端子cを接続すると、端子ad間の自己インダクタンスは (4)となる。これに対して図2のように、図1で用いたものと同じ特性を有する2個の環状鉄心にそれぞれ巻かれているコイル1の端子bとコイル2の端子cを接続した場合には、端子ad間の自己インダクタンスは(5)となる。
| (イ)(2) | \(aL_1\) | (ロ) | \(\displaystyle \frac{L_1}{\sqrt{a}}\) | (ハ) | \(\displaystyle \frac{L_1}{a^2}\) |
| (ニ)(1) | \(a^2 L_1\) | (ホ)(4) | \((a+1)^2 L_1\) | (ヘ) | \(2L_1 I_1^2\) |
| (ト) | \((a+1)L_1\) | (チ) | \(a^3 L_1\) | (リ) | \((a^3+1)L_1\) |
| (ヌ)(5) | \((a^2+1)L_1\) | (ル) | \(\sqrt{a+1}L_1\) | (ヲ)(3) | \(0\) |
| (ワ) | \(4a^2 L_1 I_1^2\) | (カ) | \(\displaystyle \frac{L_1}{a}\) | (ヨ) | \(\sqrt{a-1}L_1\) |
出典:令和3年度第一種電気主任技術者理論科目A問題問2
解説
基本的な問題にあたるかと思います。
コイル2の自己インダクタンス\(L_2\)
コイルの自己インダクタンスはコイルの巻数の二乗に比例します。
ここで、各コイルの巻数を\(N_1\)、\(N_2\)とすると、その他のパラメータに\(L_1\)と\(L_2\)で差異はないことから、\(\dfrac{L_2}{L_1} = \dfrac{N_2^2}{N_1^2}\)が成立します。
\(\dfrac{N_2}{N_1} = a \)なので、
\begin{aligned} \frac{L_2}{L_1} &= \dfrac{N_2^2}{N_1^2} \\ \frac{L_2}{L_1} &= a^2 \\ L_2 &= a^2L_1 \\ \end{aligned}
となることから、答えは(ニ)の\(a^2L_1 \)です。
相互インダクタンス\(M\)
相互インダクタンスは結合係数を\(k\)とすると
\begin{aligned} M &= k\sqrt{L_1L_2}\\ \end{aligned}
で表されます。
問題文に「各コイルに電流が流れたときには鉄心の内部にのみ磁界が発生するものとする」とあることから、漏れ磁束はなく、結合係数は1となるため\(M = \sqrt{L_1L_2}\)となります。
(2)より、\(L_2 = a^2L_1\)なので、これを代入すると
\begin{aligned} M &= \sqrt{L_1L_2}\\ &= \sqrt{L_1\cdot a^2L_1} \\ &= aL_1 \\ \end{aligned}
となるので、答えは(イ)の\(aL_1\)です。
磁界のエネルギー
与えられた式\(W = \dfrac{1}{2} L_1 I_1^2 + \dfrac{1}{2} L_2 I_2^2 + M I_1 I_2\)に\(I_1 = -a I_2\)、\(L_2 = a^2L_1 \)、\(M=aL_1\)を代入します。
\begin{aligned} W &= \dfrac{1}{2} L_1 I_1^2 + \dfrac{1}{2} L_2 I_2^2 + M I_1 I_2 \\ &= \frac{1}{2} L_1 (-aI_2)^2 + \frac{1}{2} a^2 L_1 I_2^2 + a L_1 (-aI_2) \cdot I_2 \\ &= \frac{1}{2} a^2 L_1 I_2^2 + \frac{1}{2} a^2 L_1 I_2^2 - a^2 L_1 I_2^2 \\ &= 0 \end{aligned}
よって答えは(ヲ)の\(0\)です。
図1のコイル1の端子bとコイル2の端子cを接続したときの端子ad間の自己インダクタンス
端子bと端子cを接続した場合、和動接続となりますので、コイルの巻数が\(N_2\)分増えたと解釈できます。よって、端子ad間の自己インダクタンスを\(L_{ad}\)とすると、(1)の考え方を参考にして
\begin{aligned} L_{ad} &= \dfrac{\left(N_1+N_2\right)^2}{N_1^2}L_1 \\ &= \dfrac{\left(N_1+aN_1\right)^2}{N_1^2}L_1 \\ &= \dfrac{ \left( 1+a \right)^2 \cdot N_1^2 }{N_1^2}L_1 \\ &= \left(a+1\right)^2L_1 \end{aligned}
あるいは、和動接続の式を用いて
\begin{aligned} L_{ad} &= L_1 + L_2 + 2M \\ &= L_1 + a^2L_2 + 2aL_1 \\ &= \left( a^2 + 2a + 1\right)L_1 \\ &= \left(a+1\right)^2L_1 \\ \end{aligned}
で、答えは(ホ)の\((a+1)^2 L_1\)となります。
図2のコイル1の端子bとコイル2の端子cを接続したときの端子ad間の自己インダクタンス
この時は相互インダクタンスはありませんので、自己インダクタンス\(L_{ad2}\)は各コイルのインダクタンスの和となります。よって
\begin{aligned} L_{ad} &= L_1 + L_2 \\ &= L_1 + a^2L_2 \\ &= \left( a^2 + 1\right)L_1 \\ \end{aligned}
よって答えは(ヌ)の\((a^2+1)L_1\)です。
- (1)ニ \(a^2 L_1\)
- (2)イ \(aL_1\)
- (3)ヲ \(0\)
- (4)ホ \((a+1)^2 L_1\)
- (5)ヌ \((a^2+1)L_1\)