電験一種 R3年 理論 問1
次の文章は、誘電体の近くに存在する電荷に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
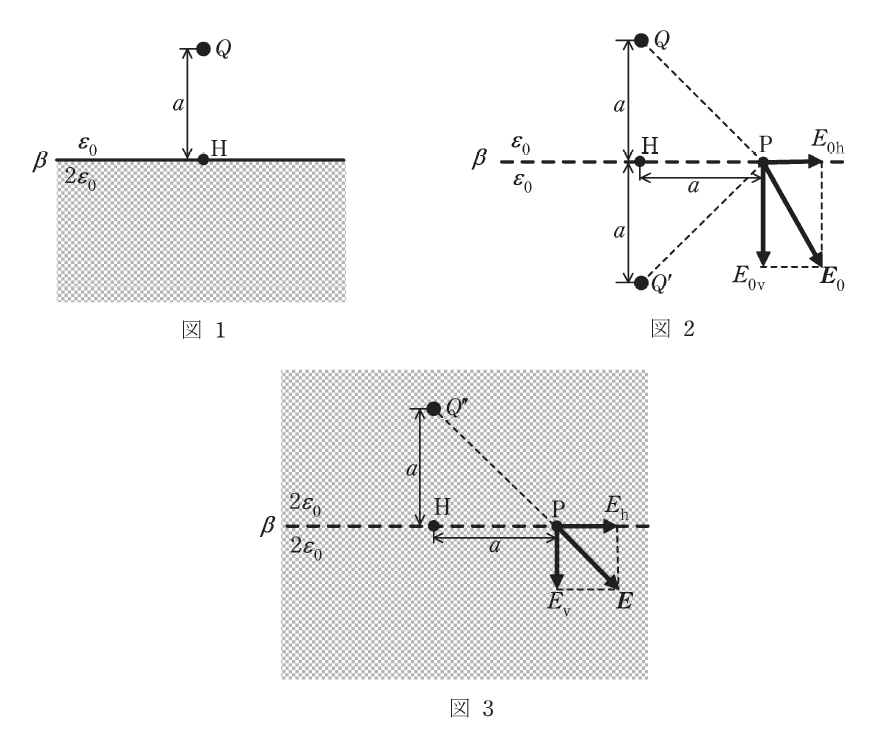
図1のように、平面\(\beta\)から上方へ距離\(a\)離れた真空中に点電荷\(Q\)を置く。\( \beta \)より上側は誘電率\(\varepsilon_0\)の真空であり、下側は誘電率\(2\varepsilon_0\)の誘電体で完全に満たされている。このとき、空間中の電界を求めるために、影像電荷の考え方を用いる。
\(\beta\)より上側の電界は、図2のように、誘電体を取り除き、\(\beta\)に対して電荷\(Q\)と対称な位置に電荷\(Q'\)を置くことで求める。\( \beta \)より下側の電界は、図3のように、全空間を誘電体で満たし、電荷\(Q\)の位置の電荷を\(Q''\)とすることで求める。
\(Q'\)及び\(Q''\)は、\(\beta\)上の任意の点において、\(\beta\)に平行な電界の成分が同じであることと、\(\beta\)に(1)な電束密度の成分が同じであることにより求められる。ただし、ここでは簡単のため、電荷\(Q\)より\(\beta\)に下ろした垂線の足Hから距離\(r\)離れた点Pを考える。
図2で、電荷\(Q\)と\(Q'\)が点Pに作る電界\(\boldsymbol{E_0}\)において、\(\beta\)に平行な成分\(E_{0h}\)と垂直な成分\(E_{0v}\)はそれぞれ
\(E_{0h} = \dfrac{Q + Q'}{8\sqrt{2} \pi \varepsilon_0 a^2}\), \(E_{0v} = \)(2)
である。ただし、\(E_{0h}\)と\(E_{0v}\)は、それぞれ点Hから点Pへ向かう方向と誘電体に進入する方向を正とする。また、図3で、電荷\(Q''\)が点Pに作る電界\(\boldsymbol{E}\)において、\(\beta\)に平行な成分\(E_h\)と垂直な成分\(E_v\)はそれぞれ
\(E_h = E_v =\dfrac{Q''}{4 \pi \cdot 2\varepsilon_0 \cdot 2a^2} \cdot \dfrac{1}{\sqrt{2}} = \dfrac{Q''}{16 \sqrt{2} \pi \varepsilon_0 a^2}\)
である。ただし、\(E_h\)と\(E_v\)の向きの定義は、\(E_{0h}\)と\(E_{0v}\)と同様である。
ここで、\(\beta\)に平行な電界の成分が同じであることにより\(E_{0h} = E_h\)が成り立ち、\(\beta\)に(1)な電束密度の成分が同じであることにより、(3)が成り立つ。これらから導かれる方程式を解くことで、置くべき影像電荷\(Q'\)と\(Q''\)をそれぞれ(4),(5)と定められる。
| (イ) | \(\displaystyle \frac{E_{0v}}{\varepsilon_0} = \frac{E_v}{2\varepsilon_0}\) | (ロ) | \(\displaystyle \dfrac{\dfrac{QQ'}{Q + Q'}}{8\sqrt{2}\pi\varepsilon_0 a^2}\) | (ハ) | \(2Q\) |
| (ニ) | \(\displaystyle \frac{2}{3}Q\) | (ホ)(4) | \(-\displaystyle \frac{1}{3}Q\) | (ヘ) | \(\varepsilon_0 E_{0h} = 2\varepsilon_0 E_h\) |
| (ト) | \(\displaystyle \frac{Q + Q'}{8\sqrt{2}\pi\varepsilon_0 a^2}\) | (チ) | \(0\) | (リ) | \(\displaystyle \frac{E_{0h}}{\varepsilon_0} = \frac{E_h}{2\varepsilon_0}\) |
| (ヌ)(1) | 垂直 | (ル) | 平行 | (ヲ)(3) | \(\varepsilon_0 E_{0v} = 2\varepsilon_0 E_v\) |
| (ワ)(5) | \(\displaystyle \frac{4}{3}Q\) | (カ) | \(-Q\) | (ヨ)(2) | \(\displaystyle \frac{Q - Q'}{8\sqrt{2}\pi\varepsilon_0 a^2}\) |
出典:令和3年度第一種電気主任技術者理論科目A問題問1
解説
電気影像法の詳細については書籍や別サイトを参照してください。
電束密度の同じ成分
\(\beta\)に垂直な電束密度の成分は連続でなければなりません。
\(\beta\)に垂直な成分\(E_{0v}\)
図2において、電荷\(Q\)が点\(P\)に作る電界の各方向の成分を\(E_{Qh}\)と\(E_{Qv}\)とすると、
\begin{aligned} E_{Qh} &= \frac{Q}{4\pi\varepsilon_0 (\sqrt{a^2 + a^2})^2} \times \frac{a}{\sqrt{a^2 + a^2}} \\ &= \frac{Q}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ E_{Qv} &= \frac{Q}{4\pi\varepsilon_0 (\sqrt{a^2 + a^2})^2} \times \frac{a}{\sqrt{a^2 + a^2}} \\ &= \frac{Q}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ \end{aligned}
となります。また、電荷\(Q'\)が点\(P\)に作る電界の各方向の成分を\(E_{Q'h}\)と\(E_{Q'v}\)とすると、垂直方向の成分の向きは\(E_{Qv}\)と逆になることに注意して
\begin{aligned} E_{Q'h} &= \frac{Q'}{4\pi\varepsilon_0 (\sqrt{a^2 + a^2})^2} \times \frac{a}{\sqrt{a^2 + a^2}} \\ &= \frac{Q'}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ E_{Q'v} &= -\frac{Q'}{4\pi\varepsilon_0 (\sqrt{a^2 + a^2})^2} \times \frac{a}{\sqrt{a^2 + a^2}} \\ &= -\frac{Q'}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ \end{aligned}
\(E_{0h}\)と\(E_{0v}\)はこれらの和になるので
\begin{aligned} E_{0h} &= E_{Qh} + E_{Q'h} = \frac{Q}{8\sqrt{2}\pi\varepsilon_0 a^2} +\frac{Q'}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ &= \frac{Q+Q'}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ E_{0v} &= E_{Qv} + E_{Q'v} = \frac{Q}{8\sqrt{2}\pi\varepsilon_0 a^2} - \frac{Q'}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ &= \frac{Q-Q'}{8\sqrt{2}\pi\varepsilon_0 a^2} \\ \end{aligned}
よって答えは(ヨ)の\(\displaystyle \frac{Q - Q'}{8\sqrt{2}\pi\varepsilon_0 a^2}\)です。
\(\beta\)に垂直な電束密度の成分が同じであることにより成り立つ関係
垂直な電束密度が等しいことから、図2の垂直な電束密度を\(D_{0v}\)、図3の垂直な電束密度を\(D_v\)とすると
\begin{aligned} D_{0v} &= D_v\\ \end{aligned}
となり、誘電率と電界を使って表現すると
\begin{aligned} \varepsilon_0 E_{0v} = 2\varepsilon_0 E_v \\ \end{aligned}
となるので、答えは(ヲ)の\(\varepsilon_0 E_{0v} = 2\varepsilon_0 E_v\)です。
影像電荷\(Q'\)
電荷\(Q''\)による電界\(E_h\)と\(E_v\)を求めます。
\begin{aligned} E_{h} &= \frac{Q''}{4\pi\cdot 2\varepsilon_0 (\sqrt{a^2 + a^2})^2} \times \frac{a}{\sqrt{a^2 + a^2}} \\ &= \frac{Q''}{16\sqrt{2}\pi\varepsilon_0 a^2} \\ E_{v} &= \frac{Q''}{4\pi\cdot 2\varepsilon_0 (\sqrt{a^2 + a^2})^2} \times \frac{a}{\sqrt{a^2 + a^2}} \\ &= \frac{Q''}{16\sqrt{2}\pi\varepsilon_0 a^2} \\ \end{aligned}
\(\beta\)に平行な電界の成分が等しいことから、\(E_{0h} = E_{h}\)なので、
\begin{aligned} E_{0h} &= E_{h} \\ \frac{Q+Q'}{8\sqrt{2}\pi\varepsilon_0 a^2} &= \frac{Q''}{16\sqrt{2}\pi\varepsilon_0 a^2} \\ 2\left( Q+Q' \right)&= Q'' \\ \end{aligned}
また、\(\beta\)に垂直な電束密度の成分が等しいことから、\(\varepsilon_0 E_{0v} = 2\varepsilon_0 E_v\)なので、
\begin{aligned} \varepsilon_0 E_{0v} &= 2\varepsilon_0 E_v \\ \frac{Q-Q'}{8\sqrt{2}\pi a^2} &= \frac{2Q''}{16\sqrt{2}\pi a^2} \\ Q-Q' &= Q'' \\ \end{aligned}
これより\(Q'\)を求めると、\(Q''\)を消去して
\begin{aligned} 2\left( Q+Q' \right)&= Q-Q' \\ 3Q' &= -Q \\ Q' &= -\frac{1}{3}Q \\ \end{aligned}
よって答えは(ホ)の\(-\displaystyle \frac{1}{3}Q\)です。
影像電荷\(Q''\)
(4)で\(Q' = -\dfrac{1}{3}Q \)であることが分かりましたので、これを\(Q-Q' = Q''\)に代入すると
\begin{aligned} Q-Q' &= Q'' \\ Q-\left( -\frac{1}{3}Q \right) &= Q'' \\ Q'' & = \frac{4}{3}Q \\ \end{aligned}
よって答えは(ワ)の\(\displaystyle \frac{4}{3}Q\)です。
- (1)ヌ 垂直
- (2)ヨ \(\displaystyle \frac{Q - Q'}{8\sqrt{2}\pi\varepsilon_0 a^2}\)
- (3)ヲ \(\varepsilon_0 E_{0v} = 2\varepsilon_0 E_v\)
- (4)ホ \(-\displaystyle \frac{1}{3}Q\)
- (5)ワ \(\displaystyle \frac{4}{3}Q\)