電験一種 R2年 理論 問5
次の文章は、三相交流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
図1のように、インダクタ\(L\)と可変抵抗\(R\)から構成されるY形不平衡負荷に、対称三相交流電源が接続されている。線間電圧の大きさは\(|\dot{E}_{ab}| = |\dot{E}_{bc}| = |\dot{E}_{ca}| = E\)、電源の角周波数は\(\omega\)である。
図1において、端子A-Bから見たテブナンの等価回路を考えれば、図2の等価回路が得られる。図2の等価回路において、インピーダンス\(\dot{Z} = \)(1)であり、電源の電圧の大きさ\(|\dot{V}| = \)(2)である。
図2において、可変抵抗\(R\)を流れる電流\(\dot{I}_R\)の大きさ\(|\dot{I}_R| = \)(3)となる。可変抵抗\(R\)で消費される有効電力\(P_R = \)(4)であり、(5)の条件が成立するとき、\(P_R\)は最大となる。
| (イ) | \(j2\omega L\) | (ロ) | \(\displaystyle \frac{\dfrac{E}{\sqrt{3}}}{ \sqrt{R^2 + (\omega L)^2}}\) | (ハ) | \(\displaystyle \frac{\dfrac{E}{2}}{ \sqrt{R^2 + (2\omega L)^2}}\) |
| (ニ) | \(R = 2\omega L\) | (ホ) | \(\displaystyle \frac{E}{2}\) | (ヘ)(3) | \(\displaystyle \frac{\dfrac{\sqrt{3}E}{2}}{ \sqrt{ R^2 + \left( \dfrac{\omega L}{2}\right)^2 } } \) |
| (ト) | \(\displaystyle \dfrac{\dfrac{RE^2}{3}}{R^2 + (\omega L)^2}\) | (チ) | \(R = \omega L\) | (リ)(5) | \(R = \displaystyle \frac{\omega L}{2}\) |
| (ヌ)(4) | \(\displaystyle \dfrac{\dfrac{3RE^2}{4}}{R^2 + \left(\dfrac{\omega L}{2} \right)^2 }\) | (ル) | \(\displaystyle \frac{\dfrac{RE^2}{4}}{R^2 + (2\omega L)^2} \) | (ヲ) | \(\displaystyle \frac{E}{\sqrt{3}}\) |
| (ワ) | \(j\omega L\) | (カ)(2) | \(\displaystyle \frac{\sqrt{3}E}{2}\) | (ヨ)(1) | \(j \displaystyle \frac{\omega L}{2}\) |
出典:令和2年度第一種電気主任技術者理論科目B問題問5
解説
問題を解くだけであれば比較的簡単なのかなと思いますが、私自身はテブナンの等価回路の電源電圧に非常に悩まされました。
等価回路におけるインピーダンス\(\dot{Z}\)
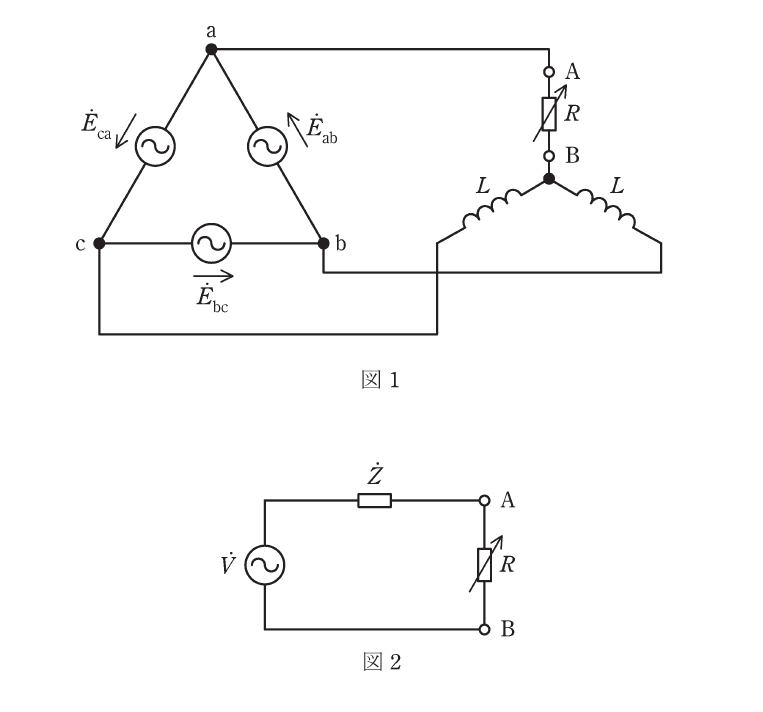
電圧源を短絡した場合、回路は図のようになります。
この時、端子A-Bから見るとインダクタンス\(L\)の並列回路なので\(\dot{Z}\)は
\begin{aligned} \dot{Z} = j \displaystyle \frac{\omega L}{2} \\ \end{aligned}
となり、答えは(ヨ)の\(j \displaystyle \frac{\omega L}{2}\)です。
電源電圧の大きさ\(|\dot{V}| \)
テブナン等価回路の電源電圧\(\dot{V} \)は端子A-Bを開放した時に現れる電圧です。これはいいと思います。
この後、ベクトル図が正三角形になり、\(\cos\dfrac{\pi}{6} = \dfrac{\sqrt{3}}{2}\)であることや、
端子Aの電位がaの電位と等しく\(\dot{E}_{ab}\)であって、端子Bの電位が\(\dfrac{\dot{E}_{bc}}{2}\)であるから
\begin{aligned} \dot{V} &= \dot{E}_{ab} + \dfrac{\dot{E}_{bc}}{2} \\ \end{aligned}
になる等の解説がありますが、いまいち理解できなかったので違った方法で考えてみたいと思います。
私は\(\dot{E}_{ca}\)がどこにいったかも分からなかったし、なぜ上の式が電圧の和になるかも理解できませんでした。
なお、これは私の解釈が多く含まれているため取り扱い注意でお願いします。
また、長くなるので試験に受かるためだけであれば答えが(カ)の\(\displaystyle \frac{\sqrt{3}E}{2}\)になることだけ覚えて読み飛ばしてください。
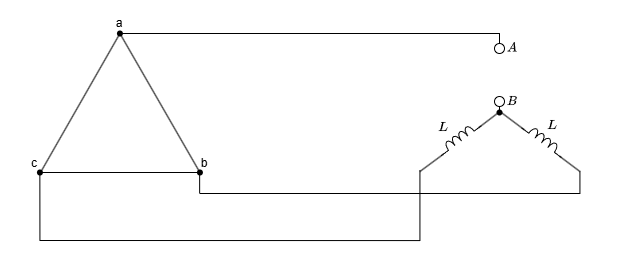
図のように、各電源によって端子A-Bにかかる電圧を考えたいと思います。
ここで、電圧はbを基準とします。なお、何を基準にしても端子A-Bの電圧は電位差なので同じ結果が得られます。
一旦、上の図の黄緑の閉路を無視して端子A-Bにかかる電圧を考えたいと思います。これを\(\dot{V_a}\)とします。
すると、下の図のようになります。なお、この時は電流が流れるルートがないことからインダクタンス\(L\)は無視しました。
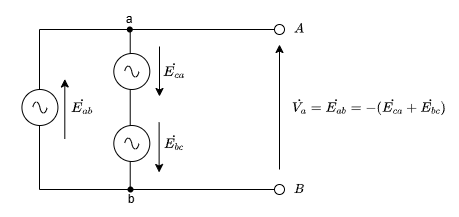
\(\dot{V}_a = \dot{E}_{ab} = -(\dot{E}_{ca} + \dot{E}_{bc}) \)となることが分かります。
対称三相交流電源なので、\( \dot{E}_{ab} + \dot{E}_{bc} + \dot{E}_{ca} = 0 \)であり、キルヒホッフの第2法則、閉じた道筋に沿って一周すると、電位の変化の合計は必ずゼロになるとも矛盾していません。
そのため、bを基準とした時の端子A-Bの電圧は\( \dot{E}_{ab} = -(\dot{E}_{ca} + \dot{E}_{bc}) \)です。
同様に、インダクタンス\(L\)が無視できない閉路による電圧を求めます。これを\(\dot{V_b}\)とします。
この時は下図のようになります。
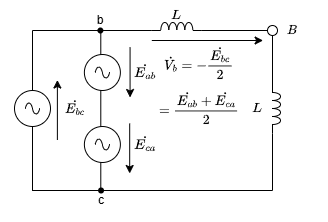
どちらもインダクタンス\(L\)なので当然半分に分圧された形となります。普段の回路であれば\(\dot{V_b} = \dfrac{\dot{E}_{bc}}{2} \)となりますが、ここではbを基準としているので電圧の正負が逆となり、
\( \dot{V}_b = - \dfrac{\dot{E}_{bc}}{2} = \dfrac{\dot{E}_{ab} + \dot{E}_{ca}}{2} \)となります。
以上より、端子A-Bの電圧は、\(\dot{V} = \dot{V_a} - \dot{V_b} \)で表されますので、これを計算すると
\begin{aligned} \dot{V} &= \dot{E}_{ab} - \left( -\frac{\dot{E}_{bc}}{2} \right) \\ &= \dot{E}_{ab} + \frac{\dot{E}_{bc}}{2} \\ \end{aligned}
や、
\begin{aligned} \dot{V} &= \dot{E}_{ab} - \left( \frac{\dot{E}_{ab} + \dot{E}_{ca}}{2} \right) \\ &= \dot{E}_{ab} - \frac{\dot{E}_{ab}}{2} - \frac{\dot{E}_{ca}}{2} \\ &= \frac{\dot{E}_{ab} - \dot{E}_{ca}}{2} \\ \end{aligned}
で表されることがわかります。
これらをベクトル図で示すと以下のようになり、\(\dot{V} = \dot{E}_{ab} + \dfrac{\dot{E}_{bc}}{2} = \dfrac{\dot{E}_{ab} - \dot{E}_{ca}}{2}\)であることが分かります。
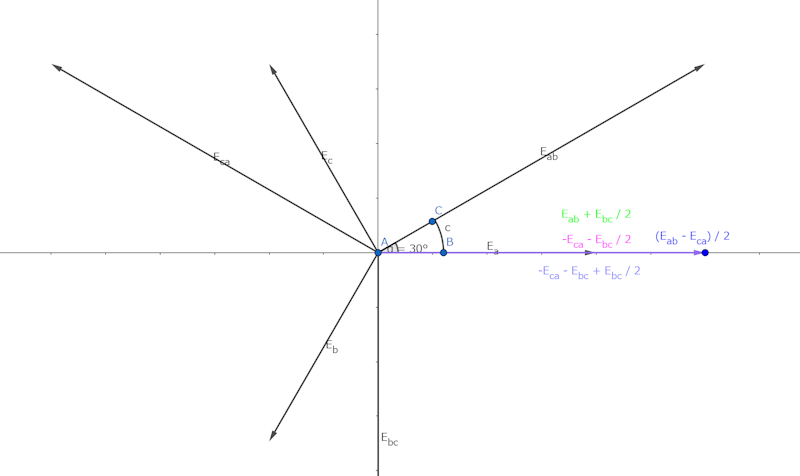
また、\(\dot{V}\)は\(\dot{E}_{ab}\)に対して\(\dfrac{\pi}{6}\)遅れであり、\(x\)軸は同じ大きさなので\(|\dot{V}| = E\cos \dfrac{\pi}{6} = \dfrac{\sqrt{3}E}{2}\)です。
ベクトルオペレータを用いて\(\dot{E}_{ab}\)を基準として\(\dot{E}_{ab}= E\)、\(\dot{E}_{bc}= a^2E\)、\(\dot{E}_{ca}= aE\)として大きさを計算してみます。
\begin{aligned} \dot{V} &= \dot{E}_{ab} + \dfrac{\dot{E}_{bc}}{2} \\ &= E + \frac{a^2 E}{2} \\ &= E \left( 1 + \frac{a^2}{2} \right)\\ &= E \left( 1 + \frac{-\frac{1}{2} - j\frac{\sqrt{3}}{2}}{2} \right) = E \left( 1 - \frac{1}{4} - j\frac{\sqrt{3}}{4} \right)\\ &= E \left( \frac{3}{4} - j\frac{\sqrt{3}}{4} \right)\\ |\dot{V}| &= E \sqrt{\left(\frac{3}{4}\right)^2 + \left(-\frac{\sqrt{3}}{4}\right)^2}\\ &= E \sqrt{\frac{9}{16} + \frac{3}{16}} = E \sqrt{\frac{12}{16}} = E \sqrt{\frac{3}{4}}\\ &= \frac{\sqrt{3}E}{2} \end{aligned}
同様に
\begin{aligned} \dot{V} &= \dfrac{\dot{E}_{ab} - \dot{E}_{ca}}{2} \\ &= \frac{E (1 - a)}{2} \\ &= \frac{E \left\{ 1 - \left(-\frac{1}{2} + j\frac{\sqrt{3}}{2}\right) \right\} }{2} = \frac{E \left( 1 + \frac{1}{2} - j\frac{\sqrt{3}}{2} \right)}{2} \\ &= \frac{E \left( \frac{3}{2} - j\frac{\sqrt{3}}{2} \right)}{2} = E \left( \frac{3}{4} - j\frac{\sqrt{3}}{4} \right) \\ &= E \left( 1 + \frac{-\frac{1}{2} - j\frac{\sqrt{3}}{2}}{2} \right) = E \left( 1 - \frac{1}{4} - j\frac{\sqrt{3}}{4} \right)\\ &= E \left( \frac{3}{4} - j\frac{\sqrt{3}}{4} \right)\\ \end{aligned}
以降の計算は同じです。
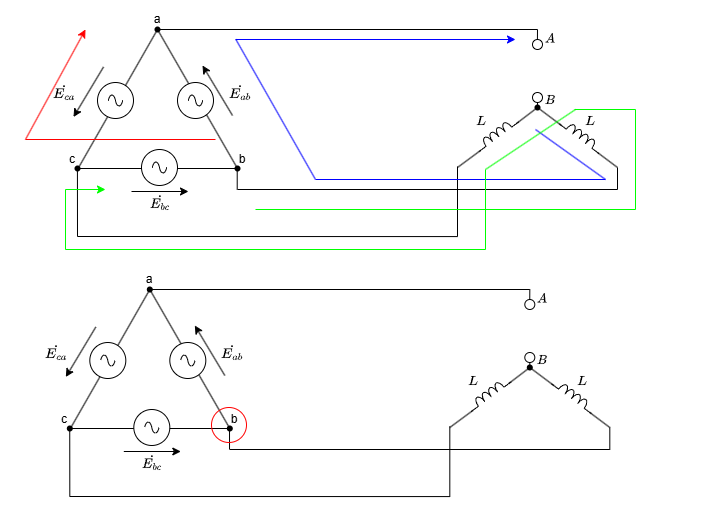
これらを1枚にまとめた画像が以下となります。
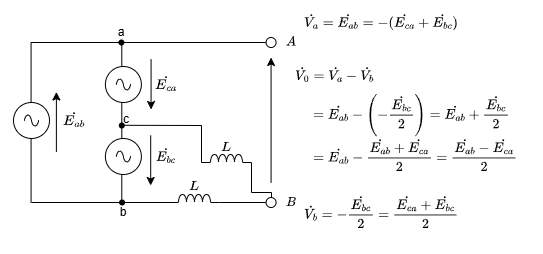
というわけで、\(\dot{E}_{ca}\)は消えたのではなく見方を変えればちゃんと出てくるということでした。
可変抵抗\(R\)を流れる電流\(\dot{I_R}\)の大きさ\(|\dot{I_R}|\)
テブナンの定理により電流を求めます。
\begin{aligned} \dot{I}_R &= \frac{\dot{V}}{R + \dot{Z}} \\ &= \frac{\dot{V}}{R + j \dfrac{\omega L}{2}} \\ |\dot{I}_R| &= \frac{|\dot{V}|}{\sqrt{R^2 + \left(\dfrac{\omega L}{2}\right)^2}} \\ |\dot{I}_R| &= \frac{\dfrac{\sqrt{3}E}{2}}{\sqrt{R^2 + \left(\dfrac{\omega L}{2}\right)^2}} \\ \end{aligned}
よって答えは(ヘ)の\(\displaystyle \frac{\dfrac{\sqrt{3}E}{2}}{ \sqrt{ R^2 + \left( \dfrac{\omega L}{2}\right)^2 } } \)です。
有効電力\(P_R\)
有効電力\(P_R\)は\( R \cdot |\dot{I}_R|^2\)で表されるので
\begin{aligned} P_R &= R \cdot |\dot{I}_R|^2 \\ &= R \left\{ \dfrac{\dfrac{\sqrt{3}E}{2}}{\sqrt{R^2 + \left(\dfrac{\omega L}{2}\right)^2}} \right\}^2 \\ &= \frac{ \dfrac{3RE^2}{4}}{R^2 + \left(\dfrac{\omega L}{2}\right)^2} \\ \end{aligned}
よって答えは(ヌ)の\(\displaystyle \dfrac{\dfrac{3RE^2}{4}}{R^2 + \left(\dfrac{\omega L}{2} \right)^2 }\)です。
\(P_R\)が最大になる条件
(4)の答えを分母、分子ともに\(R\)で割ります。
\begin{aligned} P_R = \frac{\dfrac{3E^2}{4}}{R + \dfrac{\left(\dfrac{\omega L}{2}\right)^2}{R}} \\ \end{aligned}
ここで、\(f(R)= R + \dfrac{\left(\dfrac{\omega L}{2}\right)^2}{R}\)とします。
\(R\)で微分します。
\begin{aligned} \frac{df(R)}{dR} &= \frac{d}{dR} \left( R + \dfrac{\left(\frac{\omega L}{2}\right)^2}{R} \right) \\ &= 1 - \frac{1}{R^2} \left(\dfrac{\omega L}{2}\right)^2 \\ \end{aligned}
\(=0\)とおいて極値を調べます。
\begin{aligned} 0 &= 1 - \frac{1}{R^2} \left(\dfrac{\omega L}{2}\right)^2 \\ 1 &= \frac{1}{R^2} \left(\dfrac{\omega L}{2}\right)^2 \\ R^2 &= \left(\frac{\omega L}{2}\right)^2 \\ R &= \frac{\omega L}{2} \\ \end{aligned}
試験の際はこの時点で答えを(リ)の\(R = \displaystyle \frac{\omega L}{2}\)として大丈夫です。
この解説では念のため極値が最小か最大か調べるため二階微分します。
\begin{aligned} \frac{d^2f(R)}{dR^2} &= \frac{d}{dR} \left\{ 1 - \frac{1}{R^2} \left(\dfrac{\omega L}{2}\right)^2 \right\} \\ &= - \left(\frac{\omega L}{2}\right)^2 (-2 R^{-3}) \\ & = \frac{\left(\omega L\right)^2}{2R^3} \end{aligned}
ここで、\( \omega \)、\( L \)、\( R \)いずれも正であることから、\(\dfrac{d^2f(R)}{dR^2}\)は正となりますので、\(f(R)\)は\(R = \dfrac{\omega L}{2} \)の時最小となり、この時\( P_R \)は最大となります。
参考
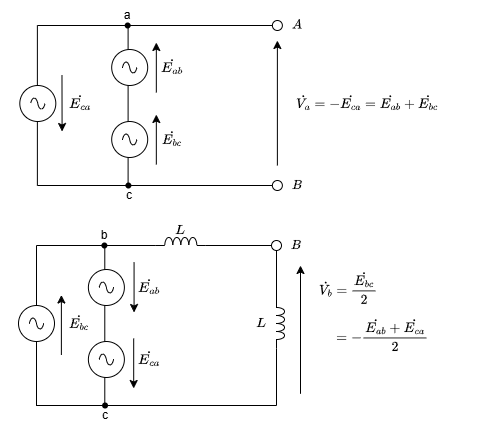
(2)においてcを基準とした時の考え方です。
計算すると\(\dot{V} = \dot{V_a} - \dot{V_b} \)は(2)と同じになることが分かります。
- (1)ヨ \(j \displaystyle \frac{\omega L}{2}\)
- (2)カ \(\displaystyle \frac{\sqrt{3}E}{2}\)
- (3)ヘ \(\displaystyle \frac{\dfrac{\sqrt{3}E}{2}}{ \sqrt{ R^2 + \left( \dfrac{\omega L}{2}\right)^2 } } \)
- (4)ヌ \(\displaystyle \dfrac{\dfrac{3RE^2}{4}}{R^2 + \left(\dfrac{\omega L}{2} \right)^2 }\)
- (5)リ \(R = \displaystyle \frac{\omega L}{2}\)