電験一種 R2年理論問4

次の文章は,回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。

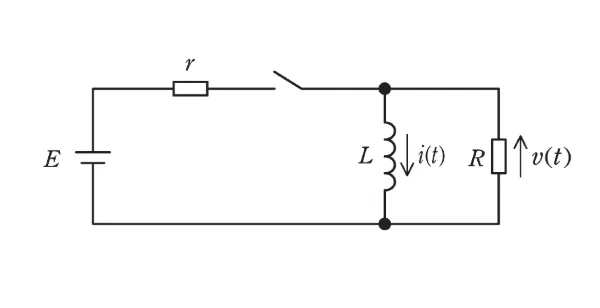
　図の回路は,直流電圧源\(E\),抵抗\(r\)及び\(R\),インダクタンス\(L\)のコイルで構成されている。時刻 \(t<0\) でスイッチは開いており,コイルの磁束は零とする \(t=0\) でスイッチを閉じた。

　\(t\geqq 0\) における抵抗Rの電圧 \(v(t)\) はコイルの電圧と等しいので,コイルの電流を \(i(t)\) とおくと,\(v(t)=\)(1)である。したがって,回路の閉路 \(E-r-R-E\) の電圧平衡の式は以下の式となる。

\(\displaystyle E=r[\frac{1}{R}\)(1)\(+i(t)]+\)(1)・・・・・・・・・①

ここで,回路の時定数を\(\tau\)とすると,①式より\(\tau=\)(2)である。時定数を使うと,\(t\geqq 0\)での抵抗Rの電圧 \(v(t)\) とコイルの電流 \(i(t)\) の式は,それぞれ,

\(v(t)=v(0)e^{-t/\tau}\) ,ただし,\(v(0)=\)(3)

\(i(t)=i(\infty)(1-e^{-t/\tau})\) ただし,\(i(\infty)=\)(4)

と表せる。

　\(t=0\) から回路が定常状態となるまでに,抵抗\(R\)が消費するエネルギーを \(J_{R}\),定常状態でコイルが保有する磁気エネルギーを \(J_{L}\) とおくと,

\(\displaystyle J_{R}=\int_{0}^{\infty}\frac{v(t)^{2}}{R}dt=\frac{1}{R}v(0)^{2}\int_{0}^{\infty}e^{-2t/\tau}dt=\frac{1}{R}v(0)^{2}\frac{\tau}{2}\)

\(\displaystyle J_{L}=\frac{1}{2}Li(\infty)^{2}\)

となる。\(J_{R}\)と\(J_{L}\)に(2),(3),(4)の式を代入すると,\(\displaystyle \frac{J_{R}}{J_{L}}\)は(5)となる。

(ｲ)	\(E\)	(ﾛ)	\(\displaystyle \frac{J_R}{J_L} = 1\)	(ﾊ)	\(\displaystyle \frac{J_R}{J_L} = \frac{R}{r}\)
(ﾆ)(2)	\(\displaystyle L\frac{R+r}{Rr}\)	(ﾎ)	\(\displaystyle \frac{E}{R}\)	(ﾍ)	\(\displaystyle \frac{L}{r}\)
(ﾄ)(1)	\(L \displaystyle \frac{d}{dt} i(t)\)	(ﾁ)(3)	\(\displaystyle \frac{ER}{R+r}\)	(ﾘ)(4)	\(\displaystyle \frac{E}{r}\)
(ﾇ)	\(\displaystyle \frac{L}{R}\)	(ﾙ)	\(Li(t)\)	(ｦ)	\(\displaystyle \frac{1}{L} \int_0^t i(\theta) d\theta\)
(ﾜ)	\(\displaystyle \frac{Er}{R}\)	(ｶ)	\(\displaystyle \frac{E}{Rr}(R+r)\)	(ﾖ)(5)	\(\displaystyle \frac{J_R}{J_L} = \frac{r}{R+r}\)

出典:令和2年度第一種電気主任技術者理論科目A問題問4

解説

慣れていれば複雑な計算をしなくとも答え自体は出せる問題なので、他の問題に時間を割くために早く終わらせたいところです。

抵抗\(R\)の電圧 \(v(t)\)

抵抗Rの電圧 \(v(t)\) はコイルの電圧と等しいので、

\(\displaystyle v(t) = L \frac{d}{dt} i(t)\)

回路の時定数\(\tau\)

問題で与えられた電圧平衡の式に(1)の答えを入れると

\(\displaystyle E = r \left[ \frac{1}{R}･ L \frac{d}{dt} i(t) + i(t) \right] + L \frac{d}{dt} i(t)\)

これを整理すると

\(\displaystyle \frac{E}{r} = \left(L･\frac{R+r}{Rr} \right)\frac{d}{dt} i(t) + i(t) \)

この時点で解答の\(\displaystyle L\frac{R+r}{Rr} \)を選択することができるかと思います。

この後は微分方程式を解いてもいいのですがラプラス変換でやります。やりやすい方でいいかと思います。

ラプラス変換すると

\(\displaystyle \frac{E}{sr} = \left(L･\frac{R+r}{Rr} \right) \{ sI(s)-i(0) \} + I(s) \)

\( i(0) \)はコイルの電流の初期値であり、\( t = 0 \)のとき\( i(0) = 0 \)なので

\begin{aligned} \frac{E}{sr} &= \left(L･\frac{R+r}{Rr} \right) sI(s) + I(s) \\ \frac{E}{sr} &= \left(sL･\frac{R+r}{Rr} + 1\right) I(s) \\ \end{aligned}

\(I(s)\)について整理すると

\begin{aligned} I(s) &= \frac{E}{sr\left(sL･\frac{R+r}{Rr} + 1\right)} \\ I(s) &= \frac{E}{r}･\frac{1}{s\left(sL･\frac{R+r}{Rr} + 1\right)} \\ \end{aligned}

\(\displaystyle \frac{1}{s\left(sL･\frac{R+r}{Rr} + 1\right)}\)を部分分数分解すると

\begin{aligned} \frac{A}{s} + \frac{B}{sL･\frac{R+r}{Rr} + 1} &= \frac{1}{s\left(sL･\frac{R+r}{Rr} + 1\right)} \\ A\left(sL･\frac{R+r}{Rr} + 1\right)+Bs &= 1 \\ \end{aligned}

よって、

\(\displaystyle A = 1\)

\begin{aligned} L･\frac{R+r}{Rr} + B &= 0 \\ B &= -L･\frac{R+r}{Rr} \\ \end{aligned}

これを代入すると、

\begin{aligned} \frac{A}{s} + \frac{B}{sL･\frac{R+r}{Rr} + 1} &= \frac{1}{s} - \frac{1}{s + \frac{Rr}{L(R+r)}} \\ \end{aligned}

となり、\( I(s) \)は

\begin{aligned} I(s) &= \frac{E}{r}･ \left\{ \frac{1}{s} - \frac{1}{s + \frac{Rr}{L(R+r)}} \right\} \\ \end{aligned}

となります。これをラプラス逆変換すると、

\begin{aligned} i(t) = \mathcal{L}^{-1} [I(s)] = \frac{E}{r}･ \left\{ 1 - e^{-\frac{Rr}{L(R+r)}t} \right\} \\ \end{aligned}

となります。時定数は\( \displaystyle \tau = L\frac{R+r}{Rr}\) です。

抵抗\(R\)の電圧\(v(0)\)

(1)より、

\(\displaystyle v(t) = L \frac{d}{dt} i(t)\)

なので、(2)で求めた\(i(t)\)を使用し計算すると

\begin{aligned} v(t) &= L \frac{d}{dt} \left\{ \frac{E}{r} \left( 1 - e^{-\frac{Rr}{L(R+r)}t} \right) \right\} \\ &= \frac{RE}{R+r} e^{-\frac{Rr}{L(R+r)}t} \\ \end{aligned}

よって、\( \displaystyle v(0) = \frac{RE}{R+r} \) です。

なお、スイッチを閉じた瞬間はコイルに電流が流れないことが分かっていれば、そこを開放として考えて、\( E \)が\( R \)と\( r \)で分圧された時\( R \)にかかる電圧を考えれば答えは出せます。

コイルの電流\(i(\infty)\)

(2)より、

\begin{aligned} i(t) = \frac{E}{r}･ \left\{ 1 - e^{-\frac{Rr}{L(R+r)}t} \right\} \\ \end{aligned}

なので、\(\displaystyle i(\infty) = \frac{E}{r} \)です。

なお、定常状態の時コイルのインピーダンスが0になることが分かっていれば、複雑な計算を必要とせず答えの\(\displaystyle \frac{E}{r} \)を出せます。

消費エネルギーの比

各エネルギーの答えが与えられているので、まず比率を求めると

\(\displaystyle \frac{J_R}{J_L} = \frac{1}{R} v(0)^2 \frac{\tau}{2}･ \frac{2}{Li(\infty)^2} = \frac{\tau}{LR} ･ \frac{v(0)^2}{i(\infty)^2} \)

\( \displaystyle \tau = L\frac{R+r}{Rr}\)なので

\(\displaystyle \frac{\tau}{LR} = L\frac{R+r}{Rr} ･ \frac{1}{LR} = \frac{R+r}{R^2r} \)

\( \displaystyle v(0) = \frac{RE}{R+r} \)、\(\displaystyle i(\infty) = \frac{E}{r} \)なので

\(\displaystyle \frac{v(0)^2}{i(\infty)^2} = \left( \frac{RE}{R+r} \right) ^2 ･ \left(\frac{r}{E} \right)^2 = \left( \frac{Rr}{R+r} \right) ^2 \)

よって、

\(\displaystyle \frac{J_R}{J_L} = \frac{\tau}{LR} ･ \frac{v(0)^2}{i(\infty)^2} = \frac{R+r}{R^2r} ･ \left( \frac{Rr}{R+r} \right) ^2 = \frac{r}{R+r} \)

(1)ト　\(L \displaystyle \frac{d}{dt} i(t)\)
(2)ニ　\(\displaystyle L\frac{R+r}{Rr}\)
(3)チ　\(\displaystyle \frac{ER}{R+r}\)
(4)リ　\(\displaystyle \frac{E}{r}\)
(5)ヨ　\(\displaystyle \frac{J_R}{J_L} = \frac{r}{R+r}\)

misobonのサイト