電験一種 R2年 理論 問2
次の文章は、アンペア(アンペール)の周回積分に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
一般に、空間上の磁界ベクトルを\( \boldsymbol{H} \)、\(C\)を閉曲線、\(d\boldsymbol{l}\)を\(C\)上の微小区間ベクトル、\(I\)を\(C\)と鎖交する電流の総量とすると、アンペアの周回積分の法則は①式のようになる。
\(\displaystyle \oint_C \boldsymbol{H} \cdot d\boldsymbol{l} = I\) …①
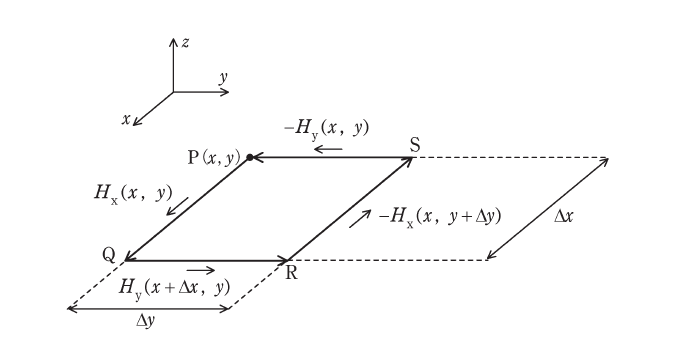
ここで、直交座標空間上において、\(z\)軸の正方向に一様な電流が流れている時の磁界\(\boldsymbol{H}\)を考える。電流の面密度は\(J_z\)である。図のように、\(z\)軸と垂直で微小な長方形の積分路を仮定する。積分路は点P\((x, y)\)から点Q, R, Sを経て点Pに戻る閉路であり、辺PQ及びRSの長さは\(\Delta x\)、辺QR及びSPの長さは\(\Delta y\)である。また、\(z\)軸方向の磁界は0であるので、\(\boldsymbol{H} = (H_x(x, y), H_y(x, y), 0)\)とし、\(x-y\)平面上で考える。
このとき、積分路PQRSを閉曲線\(C\)として①式を適用する。まず辺PQを考え、PQに平行なPQ上の磁界を\(H_x(x, y)\)と近似すると、PQに沿った\(\boldsymbol{H}\)の線積分は(1)である。同様に、辺QR, RS, SPに平行な磁界をそれぞれ\(H_y(x+\Delta x, y)\), \(-H_x(x, y+\Delta y)\), \(-H_y(x, y)\)と近似すると、①式の左辺は(2)である。一方、①式の右辺は、この積分路に鎖交する電流\(I\)なので(3)である。したがって、①式より(4)が導かれる。
\(\Delta x\), \(\Delta y\)をともに0に近づけると、電流密度ベクトルを\(\boldsymbol{J}\)としたときに(5)のように表されるアンペアの法則の微分形における\(z\)方向成分と同じ式になる。
| (イ) | \(\displaystyle \frac{H_y(x+\Delta x, y) - H_y(x, y)}{\Delta y} - \frac{H_x(x, y + \Delta y) - H_x(x, y)}{\Delta x} = J_z\) | ||||
| (ロ) | \(\displaystyle \frac{H_x(x, y)}{\Delta x} + \frac{H_y(x + \Delta x, y)}{\Delta y} - \frac{H_x(x, y + \Delta y)}{\Delta x} - \frac{H_y(x, y)}{\Delta y}\) | ||||
| (ハ) | \(H_x(x, y) \cdot \Delta y + H_y(x + \Delta x, y) \cdot \Delta x - H_x(x, y + \Delta y) \cdot \Delta y - H_y(x, y) \cdot \Delta x\) | ||||
| (ニ)(2) | \(H_x(x, y) \cdot \Delta x + H_y(x + \Delta x, y) \cdot \Delta y - H_x(x, y + \Delta y) \cdot \Delta x - H_y(x, y) \cdot \Delta y\) | ||||
| (ホ)(4) | \(\displaystyle \frac{H_y(x + \Delta x, y) - H_y(x, y)}{\Delta x} - \frac{H_x(x, y + \Delta y) - H_x(x, y)}{\Delta y} = J_z\) | ||||
| (ヘ) | \(\displaystyle \frac{H_y(x + \Delta x, y) - H_y(x, y)}{\Delta x \cdot \Delta y} - \frac{H_x(x, y + \Delta y) - H_x(x, y)}{\Delta x \cdot \Delta y} = J_z\) | ||||
| (ト)(1) | \(H_x(x, y) \cdot \Delta x\) | (チ) | \(\mathrm{div} \mathbf{H} = 0\) | (リ)(3) | \(J_z \cdot \Delta x \cdot \Delta y\) |
| (ヌ) | \(J_z\) | (ル) | \(\displaystyle \frac{H_x(x, y)}{\Delta x}\) | (ヲ)(5) | \(\mathrm{rot} \mathbf{H} = \mathbf{J}\) |
| (ワ) | \(\mathrm{rot} \mathbf{J} = \mathbf{H}\) | (カ) | \(\displaystyle \frac{J_z}{\Delta x \cdot \Delta y}\) | (ヨ) | \(H_x(x, y) \cdot \Delta y\) |
出典:令和2年度第一種電気主任技術者理論科目A問題問2
解説
一見難解ですが、電験の問題はこのような場合読解で解けるようになっていることが多いです。
PQに沿った\(\boldsymbol{H}\)の線積分
辺PQの長さが\(\Delta x\)であり、PQに平行なPQ上の磁界は\(H_x(x, y)\)なので、\(\boldsymbol{H}\)の線積分は
\(H_x(x, y) \cdot \Delta x\)
です。よって答えは(ト)です。
①式の左辺
(1)と同様の考えで、PQRSと一周しますと
\begin{aligned} \oint_C \boldsymbol{H} \cdot d\boldsymbol{l} &= H_x(x, y) \cdot \Delta x + H_y(x + \Delta x, y) \cdot \Delta y - H_x(x, y + \Delta y) \cdot \Delta x - H_y(x, y) \cdot \Delta y \\ \end{aligned}
となりますので、答えは(ニ)です。
積分路に鎖交する電流\(I\)
電流の面密度が\(J_z\)で、その鎖交面積は\(\Delta x \cdot \Delta y\)なので、電流は
\(J_z \cdot \Delta x \cdot \Delta y\)
となり、答えは(リ)です。
①より導かれる式
\(\displaystyle \oint_C \boldsymbol{H} \cdot d\boldsymbol{l} = I\)に(2)と(3)の答えを代入しますと
\begin{aligned} &H_x(x, y) \cdot \Delta x + H_y(x + \Delta x, y) \cdot \Delta y - H_x(x, y + \Delta y) \cdot \Delta x - H_y(x, y) \cdot \Delta y = J_z \cdot \Delta x \cdot \Delta y\\ &\frac{H_y(x + \Delta x, y) - H_y(x, y)}{\Delta x} - \frac{H_x(x, y + \Delta y) - H_x(x, y)}{\Delta y} = J_z \end{aligned}
となりますので、答えは(ホ)です。
\(\Delta x\)、\(\Delta y\)を0に近づけた時の式
偏微分の定義式より
\begin{aligned} \frac{\partial }{\partial x}f(x, y) = \lim_{h \to 0} \frac{f(x + h, y) - f(x, y)}{h} \\ \end{aligned}
\(\Delta x\)、\(\Delta y\)を0に近づけた時とは要するに\(H_y\)を\(x\)で、\(H_x\)を\(y\)で偏微分するということなので
\begin{aligned} \frac{\partial H_y}{\partial x} - \frac{\partial H_x}{\partial y} = J_z\\ \end{aligned}
となります。
また、アンペアの法則の微分形は
\begin{aligned} \mathrm{rot} \mathbf{H} = \mathbf{J} \\ \end{aligned}
で表されます。※(5)の答え(ヲ)
\(\mathrm{rot}\)の定義より、各方向の成分は以下のようになります。
\begin{aligned} \frac{\partial H_z}{\partial y} - \frac{\partial H_y}{\partial z} = J_x \\ \frac{\partial H_x}{\partial z} - \frac{\partial H_z}{\partial x} = J_y \\ \frac{\partial H_y}{\partial x} - \frac{\partial H_x}{\partial y} = J_z \\ \end{aligned}
\(z\)軸方向の成分の式が一致しています。
- (1)ト \(H_x(x, y) \cdot \Delta x\)
- (2)ニ \(H_x(x, y) \cdot \Delta x + H_y(x + \Delta x, y) \cdot \Delta y - H_x(x, y + \Delta y) \cdot \Delta x - H_y(x, y) \cdot \Delta y\)
- (3)リ \(J_z \cdot \Delta x \cdot \Delta y\)
- (4)ホ \(\displaystyle \frac{H_y(x + \Delta x, y) - H_y(x, y)}{\Delta x} - \frac{H_x(x, y + \Delta y) - H_x(x, y)}{\Delta y} = J_z\)
- (5)ヲ \(\mathrm{rot} \mathbf{H} = \mathbf{J}\)