電験一種 R2年 理論 問1
次の文章は、円板状の電荷分布が作り出す電界に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。なお、電位は無限遠点を基準とする。
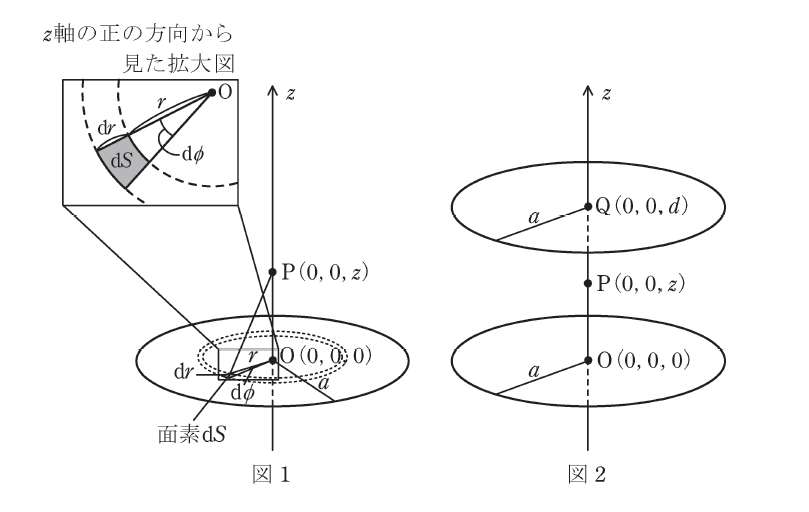
図1のように電荷が一様な面密度\(\sigma\) (ただし\(\sigma \gt 0\)とする) で分布した半径\(a\)の薄い円板が真空 (誘電率\(\varepsilon_0\)) 中に存在している。円板の厚みはその半径に比べて十分に薄いものとし、円板の軸を\(z\)軸とした円筒座標 \((r, \phi, z)\) を定め、円板の中心を原点O\((0, 0, 0)\) とする。
円板上の半径\(r\)の位置における微小半径\(dr\)、微小角度\(d\phi\)の領域 (面素) の面積は \(dS = r dr d\phi\) と表されるので、この領域に含まれる電荷が\(z\)軸上の点P\((0, 0, z)\) (ただし \(z \gt 0\) とする) に作る電位は、
\(dV = \dfrac{ dr d\phi}{4\pi\varepsilon_0} \times \)(1)
となる。よって、円板上の電荷全体が点Pに作る電位は、
\(\displaystyle V = \dfrac{1}{4\pi\varepsilon_0} \times \int_0^{2\pi} \int_0^a \)(1)\( dr d\phi \)
\(=\)(2)
となる。なお、必要であれば、
\(\dfrac{d}{dx} \sqrt{x^2 + 1} = \dfrac{x}{\sqrt{x^2 + 1}}\)
という関係式を用いても良い。
(2)の結果を用いると、このとき点Pに形成される\(z\)方向の電界は、
\(E_{z1} = -\dfrac{dV}{dz} = \)(3)
と求められる。
次に、図2に示すように点Q\((0, 0, d)\) (ただし \(d \gt 0\) とする) を中心とした半径\(a\)の十分に薄い円板上にも一様な面密度\(-\sigma\)で電荷が分布している場合を考える。点Pが点Oと点Qの間にあるとすると、点Pの\(z\)方向電界は重ね合わせにより、
\(E_{z2} = \)(4)
となる。二つの円板の半径\(a\)が円板間距離\(d\)に対して十分大きい場合には、円板間の電界は一様であるとみなせ、その大きさは(5)となる。
| (イ)(5) | \(\displaystyle \frac{\sigma}{\varepsilon_0}\) | (ロ) | \(\displaystyle \frac{\sigma}{2\varepsilon_0} \frac{z^2}{z^2 + a^2}\) | (ハ)(4) | \(\displaystyle \frac{\sigma}{2\varepsilon_0} \left[ 2 - \frac{z}{\sqrt{z^2 + a^2}} - \frac{d-z}{\sqrt{(d-z)^2 + a^2}} \right]\) |
| (ニ) | \(\displaystyle \frac{\sigma r}{z^2 + r^2}\) | (ホ) | \(\displaystyle \frac{\sigma}{2\varepsilon_0} \frac{a^2}{z^2 + a^2}\) | (ヘ)(2) | \(\displaystyle \frac{\sigma}{2\varepsilon_0} \left(\sqrt{z^2 + a^2} - z \right)\) |
| (ト)(1) | \(\displaystyle \frac{\sigma r}{\sqrt{z^2 + r^2}}\) | (チ) | \(\displaystyle \frac{\sigma}{2\varepsilon_0}\) | (リ) | \(\displaystyle \frac{\sigma}{2\varepsilon_0} \left[ \frac{z^2}{z^2 + a^2} - \frac{(d-z)^2}{(d-z)^2 + a^2} \right]\) |
| (ヌ) | \(\displaystyle \frac{\sigma}{2\varepsilon_0} z\) | (ル) | \(\displaystyle \frac{\sigma r}{(z^2 + r^2)^{\frac{3}{2}}}\) | (ヲ) | \(\displaystyle \frac{\sigma}{2\varepsilon_0} \left[ \frac{a^2}{z^2 + a^2} - \frac{a^2}{(d-z)^2 + a^2} \right]\) |
| (ワ) | \(0\) | (カ) | \(\displaystyle \frac{\sigma}{2\epsilon_0} a\) | (ヨ)(3) | \(\displaystyle \frac{\sigma}{2\epsilon_0} \left( 1 - \frac{z}{\sqrt{z^2 + a^2}} \right)\) |
出典:令和2年度第一種電気主任技術者理論科目A問題問1
解説
微分積分が苦手でなければ解けると思いますが、本番ではどのくらい時間を要するか読めないことから後回しにする人が多いと思われる問題です。
電荷が\(z\)軸上の点\(P\)に作る電位
図1の微小面積における微小電荷\(dQ\)は電荷の面密度が\(\sigma\)なので
\(\displaystyle dQ = \sigma dS = \sigma rdrd\phi\)
で表されます。また、\(dQ\)から点\(P\)までの距離\(l\)は
\(\displaystyle l = \sqrt{r^2 + z^2} \)
です。
無限遠点を基準とした時の点電荷の電位は
\( V = \dfrac{1}{4\pi\varepsilon_0} \dfrac{Q}{r} \quad (rは距離で上のrとは異なる) \)
ですから、今回のパラメータをあてはめると、微小電位\(dV\)は
\begin{aligned} dV &= \frac{dQ}{4\pi\varepsilon_0 l} \\ &= \frac{\sigma r dr d\phi}{4\pi\varepsilon_0 \sqrt{r^2 + z^2}} \\ &= \frac{dr d\phi}{4\pi\varepsilon_0} \times \frac{\sigma r}{\sqrt{z^2 + r^2}} \\ \end{aligned}
となるので、答えは(ト)の\(\displaystyle \frac{\sigma r}{\sqrt{z^2 + r^2}}\)です。
円板上の電荷全体が点\(P\)に作る電位
問題の式に(1)の答えを入れると
\begin{aligned} V &= \frac{1}{4\pi\varepsilon_0} \times \int_{0}^{2\pi} \int_{0}^{a} \frac{\sigma r}{\sqrt{z^2 + r^2}} dr d\phi \\ \end{aligned}
となりますので、これを計算します。
問題文に公式が与えられていますが、それを使った解き方は参考書にもあると思うので別の置換積分で解きます。
\begin{aligned} \int_{0}^{a} \frac{\sigma r}{\sqrt{z^2 + r^2}} dr \\ \end{aligned}
\(u=z^2+r^2\)とおきます。このとき、\(\dfrac{du}{dr}=2r\)なので、\(rdr= \dfrac{1}{2}du\)です。
また、積分範囲は\(r=0\)のとき\(z^2\)、\(r=a\)のとき\(z^2 + a^2\)となります。以上より、内側の積分は
\begin{aligned} &\frac{\sigma}{2} \int_{z^2}^{z^2 + a^2} \frac{1}{\sqrt{u}} du \\ =& \frac{\sigma}{2} \left[ \frac{u^{-\frac{1}{2} + 1}}{-\frac{1}{2} + 1} \right]_{z^2}^{z^2 + a^2}\\ =& \frac{\sigma}{2} \left[ \frac{u^{\frac{1}{2}}}{\frac{1}{2}} \right]_{z^2}^{z^2 + a^2} \\ =& \sigma \left[ \sqrt{u} \right]_{z^2}^{z^2 + a^2} \\ =& \sigma \left( \sqrt{z^2 + a^2} - \sqrt{z^2} \right) \\ =& \sigma \left( \sqrt{z^2 + a^2} - |z| \right) \\ =& \sigma \left( \sqrt{z^2 + a^2} - z \right) \quad (z>0) \\ \end{aligned}
となります。全体は
\begin{aligned} V &= \frac{1}{4\pi\varepsilon_0} \times \int_{0}^{2\pi} \int_{0}^{a} \frac{\sigma r}{\sqrt{z^2 + r^2}} dr d\phi \\ &= \frac{1}{4\pi\varepsilon_0} \times \int_{0}^{2\pi} \sigma \left( \sqrt{z^2 + a^2} - z \right) d\phi \\ &= \frac{\sigma (\sqrt{z^2 + a^2} - z)}{4\pi\varepsilon_0} \int_{0}^{2\pi} d\phi \\ &= \frac{\sigma (\sqrt{z^2 + a^2} - z)}{4\pi\varepsilon_0} \times 2\pi \\ &= \frac{\sigma }{2\varepsilon_0} (\sqrt{z^2 + a^2} - z)\\ \end{aligned}
よって、答えは(ヘ)の\(\displaystyle \frac{\sigma}{2\varepsilon_0} \left(\sqrt{z^2 + a^2} - z \right)\)です。
点Pに形成される\(z\)方向電界
\(\boldsymbol{E} = -\nabla V \)であり、問題文にある通り\(z\)方向の電界は\(E_{z1} = -\dfrac{\partial V}{\partial z}\)となりますので、これを計算します。
\begin{aligned} E_{z1} &= -\frac{\partial V}{\partial z} \\ &= -\frac{\partial}{\partial z} \left[ \frac{\sigma}{2\varepsilon_0} (\sqrt{z^2 + a^2} - z) \right] \\ &= -\frac{\sigma}{2\varepsilon_0} \frac{\partial}{\partial z} (\sqrt{z^2 + a^2} - z) \\ & = -\frac{\sigma}{2\varepsilon_0} \left( \frac{z}{\sqrt{z^2 + a^2}} - 1 \right) \\ &= \frac{\sigma}{2\varepsilon_0} \left( 1 - \frac{z}{\sqrt{z^2 + a^2}} \right) \\ \end{aligned}
よって、答えは(ヨ)の\(\displaystyle \frac{\sigma}{2\varepsilon_0} \left( 1 - \frac{z}{\sqrt{z^2 + a^2}} \right)\)です。
点Qに円板がある場合の\(z\)方向電界
上の円板による電界を\(E_{z1}'\)とします。この時、\(E_{z1}\)の\(z\)に相当する部分が\(d-z\)になり、また電荷の面密度が\(-\sigma\)であることから点Pにおいては下の円板による電界と向きが同じになるので
\begin{aligned} E_{z1}' = \frac{\sigma}{2\varepsilon_0} \left( 1 - \frac{d - z}{\sqrt{(d - z)^2 + a^2}} \right) \\ \end{aligned}
となります。合成電界\(E_{z2}\)は重ね合わせにより\(E_{z1} + E_{z1}'\)となるので
\begin{aligned} E_{z2} &= E_{z1} +E_{z1}' \\ &= \frac{\sigma}{2\varepsilon_0} \left( 1 - \frac{z}{\sqrt{z^2 + a^2}} \right) + \frac{\sigma}{2\varepsilon_0} \left[ 1 - \frac{d - z}{\sqrt{(d - z)^2 + a^2}} \right] \\ &= \frac{\sigma}{2\varepsilon_0} \left[ 1 - \frac{z}{\sqrt{z^2 + a^2}} + 1 - \frac{d - z}{\sqrt{(d - z)^2 + a^2}} \right] \\ &= \frac{\sigma}{2\varepsilon_0} \left[ 2 - \frac{z}{\sqrt{z^2 + a^2}} - \frac{d - z}{\sqrt{(d - z)^2 + a^2}} \right] \\ \end{aligned}
よって答えは(ハ)の\(\displaystyle \frac{\sigma}{2\varepsilon_0} \left[ 2 - \frac{z}{\sqrt{z^2 + a^2}} - \frac{d-z}{\sqrt{(d-z)^2 + a^2}} \right]\)です。
二つの円板の半径aが円板間距離dに対して十便に大きい場合の電界
\(a \to \infty\)の極限を考えます。
\begin{aligned} \lim_{a \to \infty} E_{z2} &= \lim_{a \to \infty} \left\{ \frac{\sigma}{2\varepsilon_0} \left[ 2 - \frac{z}{\sqrt{z^2 + a^2}} - \frac{d - z}{\sqrt{(d - z)^2 + a^2}} \right] \right\} \\ & = \frac{\sigma}{2\varepsilon_0} [2 - 0 - 0]\\ &= \frac{\sigma}{\varepsilon_0}\\ \end{aligned}
となり、答えは(イ)の\(\displaystyle \frac{\sigma}{\varepsilon_0}\)で、電界は一様となります。
- (1)ト \(\displaystyle \frac{\sigma r}{\sqrt{z^2 + r^2}}\)
- (2)ヘ \(\displaystyle \frac{\sigma}{2\varepsilon_0} \left(\sqrt{z^2 + a^2} - z \right)\)
- (3)ヨ \(\displaystyle \frac{\sigma}{2\varepsilon_0} \left( 1 - \frac{z}{\sqrt{z^2 + a^2}} \right)\)
- (4)ハ \(\displaystyle \frac{\sigma}{2\varepsilon_0} \left[ 2 - \frac{z}{\sqrt{z^2 + a^2}} - \frac{d-z}{\sqrt{(d-z)^2 + a^2}} \right]\)
- (5)イ \(\displaystyle \frac{\sigma}{\varepsilon_0}\)