電験一種 R1年 理論 問5
次の文章は、三相交流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
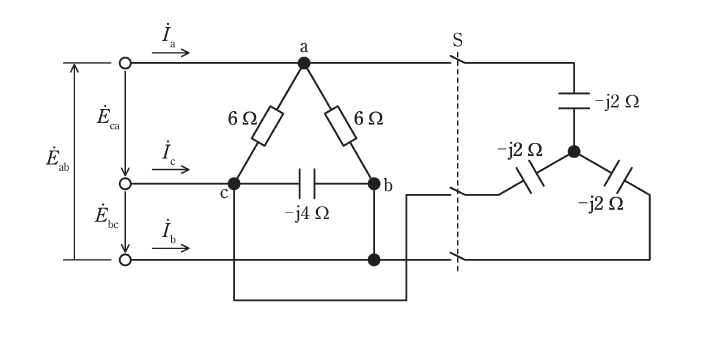
図のように、実効値が100Vである対称三相交流電圧が△形不平衡負荷とY形平衡負荷からなる回路に印加されている。図の各線間電圧は\(\dot{E}_{ab} = 100 \angle 0^\circ\) [V]を基準に、\(\dot{E}_{bc} = a^2 \dot{E}_{ab}\)、\(\dot{E}_{ca} = a \dot{E}_{ab}\)とする。ただし、\(a\)は複素数で\(a = e^{j \frac{2 \pi}{3}}\)である。
スイッチSを開き、Y形平衡負荷が接続されていない状態で△形不平衡負荷の無効電力の大きさ\(Q\)を求めると、\(Q = \)(1) kvarとなる。
次に、スイッチSを閉じ、△形不平衡負荷にY形平衡負荷が接続された場合の線電流を求める。Y形平衡負荷を△形に変換して解くと、\(\dot{I}_a = \)(2) A、\(\dot{I}_b = \)(3) A、\(\dot{I}_c = \)(4) Aとなる。また、回路全体で消費される有効電力\(P\)は\(P = \)(5) kWとなる。
| (イ) | \(1.4\) | (ロ) | \(4.1 - j19.4\) | (ハ)(2) | \(39.4 + j10.6\) | (ニ) | \(3.7\) |
| (ホ) | \(-26.9 + j58.9\) | (ヘ)(5) | \(3.3\) | (ト) | \(68.3 + j60.6\) | (チ) | \(-2.3 - j58.3\) |
| (リ)(1) | \(2.5\) | (ヌ)(4) | \(-58.9 + j26.9\) | (ル) | \(0.7\) | (ヲ)(3) | \(19.4 - j37.5\) |
| (ワ) | \(-66.0 - j2.3\) | (カ) | \(22.8 - j39.3\) | (ヨ) | \(6.6\) |
出典:令和1年度第一種電気主任技術者理論科目B問題問5
解説
順を追って解いていけば解けると思いますが、計算が面倒な問題です。
Y形平衡負荷が接続されていない状態の△形不平衡負荷の無効電力の大きさ\(Q\)
線間電圧の大きさが100で負荷が4Ωのコンデンサなので、無効電力は\(Q= \dfrac{100^2}{4} = 2500 \)となります。よって答えは(リ)の\(2.5\) kvarです。
b-c間に流れる電流を\( \dot{I}_{bc} \)として遅れ無効電力を正としたときのb-c間の皮相電力を計算してみますと、
\begin{aligned} \dot{E}_{bc} \bar{\dot{I}_{bc}} &= \dot{E}_{bc} \left( \frac{ \bar{\dot{E}_{bc}}}{j4} \right) \\ &= \frac{ |\dot{E}_{bc}|^2}{j4} \\ &= \frac{ 10000}{j4} \\ &= -j2500 \end{aligned}
となります。これからも無効電力が2.5kvarで進みであることが分かります。
電流\(\dot{I_a}\)
問題文にある通りにY型平衡負荷をΔ型に変換すると、各負荷は\(-j2 \times 3 = -j6 \)となります。
不平衡負荷の各電流を\(\dot{I_{ab}}\)、\(\dot{I_{bc}}\)、\(\dot{I_{ca}}\)として、平衡負荷の各電流を\(\dot{I_{Sab}}\)、\(\dot{I_{Sbc}}\)、\(\dot{I_{Sca}}\)とすると以下が成り立ちます。
\begin{aligned} \dot{I_a} &= \dot{I_{ab}} - \dot{I_{ca}} + \dot{I_{Sab}} - \dot{I_{Sca}} \\ \dot{I_b} &= \dot{I_{bc}} - \dot{I_{ab}} + \dot{I_{Sbc}} - \dot{I_{Sab}} \\ \dot{I_c} &= \dot{I_{ca}} - \dot{I_{bc}} + \dot{I_{Sca}} - \dot{I_{Sab}} \\ \end{aligned}
各電流を求めます。
\begin{aligned} \dot{I_{ab}} &= \frac{\dot{E}_{ab}}{6} \\ \dot{I_{bc}} &= \frac{a^2\dot{E}_{ab}}{-j4} \\ \dot{I_{ca}} &= \frac{a\dot{E}_{ab}}{6} \\ \dot{I_{Sab}}&= \frac{\dot{E}_{ab}}{-j6} \\ \dot{I_{Sbc}}&= \frac{a^2\dot{E}_{ab}}{-j6} \\ \dot{I_{Sca}}&= \frac{a\dot{E}_{ab}}{-j6} \\ \end{aligned}
先ほどの式に代入し計算します。
\begin{aligned} \dot{I_a} &= \frac{\dot{E}_{ab}}{6} - \frac{a\dot{E}_{ab}}{6} +\frac{\dot{E}_{ab}}{-j6} - \frac{a\dot{E}_{ab}}{-j6} \\ &= 100 \left\{ \frac{1}{6} - \frac{a}{6} + \frac{1}{-j6} - \frac{a}{-j6} \right\} \\ &= \frac{50}{3} \left\{ 1 - a + j - ja \right\} \\ &= \frac{50}{3} \left\{ 1 + \frac{1}{2} - j\frac{\sqrt{3}}{2} + j - \left(-\frac{j}{2} + j^2\frac{\sqrt{3}}{2}\right) \right\} \\ &= \frac{50}{3} \left\{ \frac{3 + \sqrt{3}}{2} + j\frac{3 - \sqrt{3}}{2} \right\} \\ &\fallingdotseq 39.4 + j10.6 \\ \end{aligned}
よって答えは(ハ)の\(39.4 + j10.6\)です。
なお、実部と虚部それぞれにおいて同じ選択肢が存在しないため、片方を無視して計算するのも方法としてはありかと思います。(ただし、当然誤るリスクはあがるので、時間との相談かと思います。)
電流\(\dot{I_b}\)
同様に、電流\(\dot{I_b}\)は
\begin{aligned} \dot{I_b} &= \dot{I_{bc}} - \dot{I_{ab}} + \dot{I_{Sbc}} - \dot{I_{Sab}} \\ &= \frac{a^2 \dot{E}_{ab}}{-j4} - \frac{\dot{E}_{ab}}{6} + \frac{a^2 \dot{E}_{ab}}{-j6} - \frac{\dot{E}_{ab}}{-j6} \\ &= \frac{ja^2 \dot{E}_{ab}}{4} - \frac{\dot{E}_{ab}}{6} + \frac{ja^2 \dot{E}_{ab}}{6} - \frac{j\dot{E}_{ab}}{6} \\ &= 100 \left( \frac{ja^2}{4} - \frac{1}{6} + \frac{ja^2}{6} - \frac{j}{6} \right) \\ &= 100 \left( -\frac{1}{6} + j\frac{a^2}{4} + j\frac{a^2}{6} - j\frac{1}{6} \right) \\ &= 100 \left\{ -\frac{1}{6} + \frac{1}{4} \left(\frac{\sqrt{3}}{2} - j\frac{1}{2}\right) + \frac{1}{6} \left(\frac{\sqrt{3}}{2} - j\frac{1}{2}\right) - j\frac{1}{6} \right\} \\ &= 100 \left( -\frac{1}{6} + \frac{\sqrt{3}}{8} - j\frac{1}{8} + \frac{\sqrt{3}}{12} - j\frac{1}{12} - j\frac{1}{6} \right) \\ &= 100 \left( \frac{-4 + 5\sqrt{3}}{24} - j\frac{3}{8} \right) \\ &\fallingdotseq 19.4 - j37.5 \end{aligned}
よって答えは(ヲ)の\(19.4 - j37.5\)です。
電流\(\dot{I_c}\)
3つ真面目に計算してると時間が足りなくなるので、ここは\( \dot{I_c} = -\dot{I_a} - \dot{I_b} \)で計算するのがいいと思われます。
残りの2つが間違っていない前提となるので、とりあえず上記で答えを求めて時間が余るなら検算として各電流を用いて解くのがベターでしょう。
\begin{aligned} \dot{I_c} &= -\dot{I_a} - \dot{I_b} \\ &\fallingdotseq -39.4 - j10.6 - 19.4 + j37.5 \\ &\fallingdotseq -58.8 + j26.9 \\ \end{aligned}
小数点のところでズレはあるものの、(ヌ)の\(-58.9 + j26.9\)が答えになることは分かるかと思います。
回路全体で消費される有効電力\(P\)
有効電力を消費するものはa-b、c-a間の6Ωの抵抗しかありません。よって
\begin{aligned} P &= \frac{|\dot{E}_{ab}|^2}{6} + \frac{|\dot{E}_{ca}|^2}{6} \\ &= \frac{10000}{6} + \frac{10000}{6} \\ &\fallingdotseq 3333.3 \\ \end{aligned}
よって答えは(ヘ)の\(3.3\) kWです。
- (1)リ \(2.5\)
- (2)ハ \(39.4 + j10.6\)
- (3)ヲ \(19.4 - j37.5\)
- (4)ヌ \(-58.9 + j26.9\)
- (5)ヘ \(3.3\)