電験一種 R1年 理論 問3
次の文章は、直流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
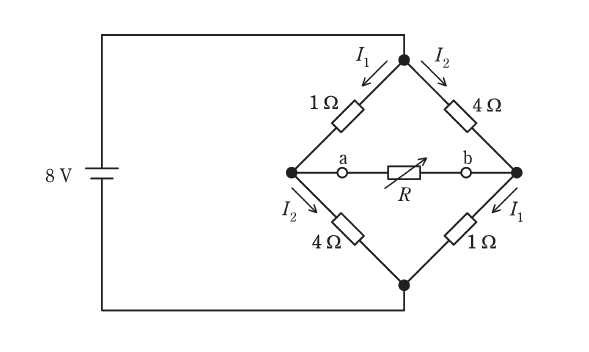
図の回路において、テブナンの定理に基づいて端子a-bから見た等価回路を考えれば、可変抵抗\(R\)の値が\(R = \)(1)Ωのとき可変抵抗\(R\)を流れる電流は0.5Aとなり、また、可変抵抗\(R\)の値が\(R = \)(2) Ωのとき可変抵抗\(R\)で消費される電力は最大となることがわかる。
図の回路において、電圧源から見た回路の合成抵抗\(R_0\)は、可変抵抗\(R\)を用いて\(R_0 = \)(3) [Ω]と表せる。また、可変抵抗\(R\)の値を\(R = \)(4) Ωとすれば、電圧源から見た回路の合成抵抗\(R_0\)の値は可変抵抗\(R\)の値と同じ値、すなわち\(R_0 = \)(4)となる。可変抵抗\(R\)の値を\(R = \)(4)としたとき、図に示す電流\(I_1\)は、\(I_1 = \) (5)Aとなる。
| (イ) | \(1\) | (ロ) | \(\displaystyle \frac{2}{3}\) | (ハ) | \(\displaystyle \frac{4}{5}\) | (ニ) | \(\displaystyle \frac{5R+1}{R+5}\) |
| (ホ)(2) | \(\displaystyle \frac{8}{5}\) | (ヘ)(1) | \(8\) | (ト) | \(\displaystyle \frac{4}{3}\) | (チ) | \(\displaystyle \frac{2R+9}{R+2}\) |
| (リ)(3) | \(\displaystyle \frac{5R+8}{2R+5}\) | (ヌ) | \(\displaystyle \frac{6}{5}\) | (ル)(4) | \(2\) | (ヲ)(5) | \(\displaystyle \frac{8}{3}\) |
| (ワ) | \(12\) | (カ) | \(3\) | (ヨ) | \(10\) |
出典:令和1年度第一種電気主任技術者理論科目A問題問3
解説
テブナンの定理を使用した基本的な問題です。
可変抵抗を流れる電流を0.5Aとする可変抵抗の値\(R\)
端子a-bの開放電圧\(V_0\)を求めます。端子aの電圧を\(V_a\)、端子bの電圧を\(V_b\)とすると
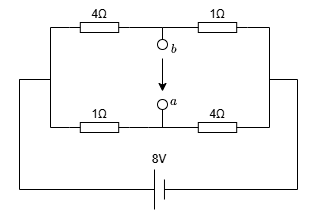
\begin{aligned} V_a &= 8 \times \frac{4}{1 + 4} = 6.4 \\ V_b &= 8 \times \frac{1}{4 + 1} = 1.6 \\ V_{0} &= V_a - V_b \\ &= 6.4 - 1.6 = 4.8 \\ \end{aligned}
となり、開放電圧は4.8Vとなります。
次に、端子a-bからみた電源側の合成抵抗\(R_{ab}\)は
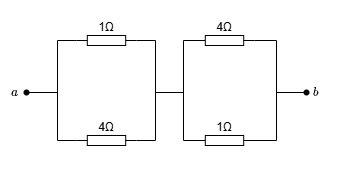
\begin{aligned} R_{ab} &=\frac{4 \times 1}{4 + 1} + \frac{1 \times 4}{1 + 4} \\ &= 0.8 + 0.8 = 1.6 \\ \end{aligned}
端子a-bを流れる電流が0.5Aとなる時の抵抗\(R\)は
\begin{aligned} I &= \frac{V_0}{R_{ab}+ R} \\ 0.5 &= \frac{V_0}{R_{ab}+ R} \\ 0.5 &= \frac{4.8}{1.6+ R} \\ R &= 8 \\ \end{aligned}
となるので、答えは(ヘ)の\(8\)です。
可変抵抗で消費される電力が最大になる時の\(R\)
(1)で端子a-bから見た合成抵抗が1.6と分かっているので、この時点で(ホ)の\(\displaystyle \frac{8}{5}\)としいいです。
念のため計算してみます。
\begin{aligned} P &= RI^2 \\ &= \frac{R \cdot (4.8)^2}{(1.6+ R)^2} \\ &= \frac{23.04 R}{R^2 + 3.2R + 2.56} \\ &= \frac{23.04}{R + 3.2 + \dfrac{2.56}{R}} \\ \end{aligned}
分母をRで微分して、傾きが0になるところを求めます。
\begin{aligned} g(R) &= R + 3.2 + \frac{2.56}{R} \\ \frac{dg}{dR} &= 1 - \frac{2.56}{R^2} = 0\\ R^2 &= 2.56 \\ R &= 1.6 \\ \end{aligned}
答えと一致することが分かります。(二階微分省略)
電圧源から見た回路の合成抵抗\(R_0\)
電圧源から見た回路の合成抵抗\(R_0\)は\( \dfrac{8}{I_1 + I_2} \)なので、\(I_1 \)と\( I_2\)を求めます。
下図のような閉回路を考えます。
以下が成立します。
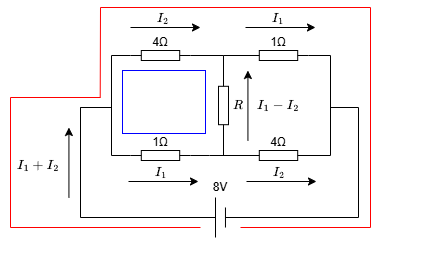
\begin{aligned} 8 &= 4I_2 + I_1 \\ 0 &= I_1 + R(I_1 - I_2) - 4I_2 \\ \end{aligned}
これを解きます。
\begin{aligned} 8 &= I_1 + 4I_2 \\ I_1 &= 8 - 4I_2 \\ \end{aligned}
\(I_2\)を求めます。
\begin{aligned} 0 &= (1 + R)I_1 - (R + 4)I_2 \\ 0&= (1 + R)(8 - 4I_2) - (R + 4)I_2 \\ 0&= 8 + 8R - (4 + 4R + R + 4)I_2 \\ I_2 &= \frac{8 + 8R}{5R + 8} \\ \end{aligned}
\(I_1\)を求めます。
\begin{aligned} I_1 &= 8 - 4 \left( \frac{8 + 8R}{5R + 8} \right) \\ &= \frac{8(5R + 8)}{5R + 8} - \frac{32(1 + R)}{5R + 8} \\ &= \frac{40R + 64 - 32 - 32R}{5R + 8} \\ &= \frac{8R + 32}{5R + 8}\\ \end{aligned}
\(I_1+I_2\)を求めます。
\begin{aligned} I_1 + I_2 &= \frac{8R + 32}{5R + 8} + \frac{8 + 8R}{5R + 8} \\ &= \frac{16R + 40}{5R + 8}\\ \end{aligned}
\(R_0\)を求めます。
\begin{aligned} R_0 &= \frac{8}{I_1 + I_2} \\ &= \frac{8}{\dfrac{16R + 40}{5R + 8}} \\ &= \frac{8(5R + 8)}{16R + 40} \\ & = \frac{5R + 8}{2R + 5} \\ \end{aligned}
よって答えは(リ)の\(\displaystyle \frac{5R+8}{2R+5}\)です。
電圧源から見た回路の合成抵抗と可変抵抗が一致する時の可変抵抗
要するに\( R= \dfrac{5R + 8}{2R + 5} \)ということなのでこれを解きます。
\begin{aligned} R &= \dfrac{5R + 8}{2R + 5} \\ 2R^2 + 5R &= 5R + 8\\ 2R^2 &= 8 \\ R^2 &= 4 \\ R &= 2 \\ \end{aligned}
よって答えは(ル)の\(2\)です。
可変抵抗が\(2\)Ωの時の電流\(I_1\)
(3)で求めた電流\(I_1\)に(4)で求めた可変抵抗\(R\)を代入します。
\begin{aligned} I_1 &= \frac{8R + 32}{5R + 8} \\ &= \frac{8 \times 2 + 32}{5 \times 2 + 8} \\ &= \frac{48}{18} \\ &= \frac{8}{3} \\ \end{aligned}
よって答えは(ヲ)の\(\displaystyle \frac{8}{3}\)です。
- (1)ヘ \(8\)
- (2)ホ \(\displaystyle \frac{8}{5}\)
- (3)リ \(\displaystyle \frac{5R+8}{2R+5}\)
- (4)ル \(2\)
- (5)ヲ \(\displaystyle \frac{8}{3}\)