電験一種 R1年 理論 問2
次の文章は、磁界によって生じる力に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。なお、\(\mu_0\)は真空の透磁率である。
図に示すような半径\(a\)、長さ\(b\)、巻数\(N\)の空心ソレノイドを考える。ただし、\(a << b\)であり、ソレノイドには一定の電流\(I\)が流れている。ソレノイドの内部には軸方向の磁束密度が一様に形成されており、ソレノイドの外部では磁束密度は零と仮定する。ソレノイド内部の磁束密度の大きさ\(B\)は、
\(B = \)(1)
と表されるので、ソレノイドのインダクタンスは\(L = \)(2)となる。
仮想変位の原理を用いて、ソレノイドを流れる電流\(I\)に働く磁界の力を求める。ソレノイド内部に蓄積された磁界のエネルギーは\(W = \)(3)となるので、ソレノイドの軸方向に働く力\(F\)は、電流一定の条件下で磁界のエネルギー\(W\)を長さ\(b\)で偏微分することで求められる。この力は磁束密度\(B\)を用いて、
\(F = \dfrac{\partial W}{\partial b} = \dfrac{B^2}{2 \mu_0} \times\)(4)
と表され、ソレノイドの(5)方向に働く。\(\dfrac{B^2}{2 \mu_0}\)は単位面積あたりに働くマクスウェルの応力と呼ばれる。 出典:令和1年度第一種電気主任技術者理論科目A問題問2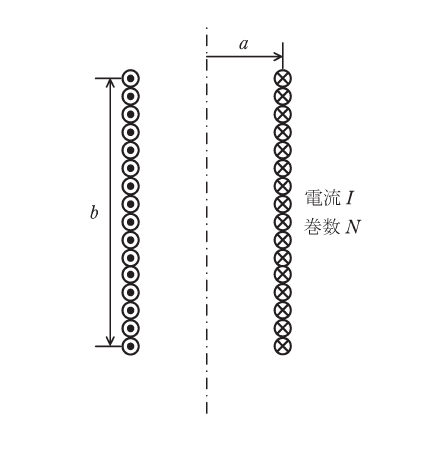
(イ)
\(\displaystyle \frac{\mu_0 \pi a^2 N}{b}\)
(ロ)
\(\displaystyle \frac{\mu_0 NI}{2b}\)
(ハ)(1)
\(\displaystyle \frac{\mu_0 NI}{b}\)
(ニ)
\(\displaystyle \frac{\mu_0 \pi a^2 N^2 I^2}{2b^2}\)
(ホ)
\(\displaystyle \frac{\mu_0 \pi a^2 NI^2}{2b}\)
(ヘ)(3)
\(\displaystyle \frac{\mu_0 \pi a^2 N^2 I^2}{2b}\)
(ト)
\(2\pi ab\)
(チ)
径を拡げる
(リ)
長さを伸ばす
(ヌ)
\(\displaystyle \frac{2\mu_0 NI}{b}\)
(ル)(2)
\(\displaystyle \frac{\mu_0 \pi a^2 N^2}{b}\)
(ヲ)
\(\pi a^2\)
(ワ)(5)
長さを縮める
(カ)(4)
\(-\pi a^2\)
(ヨ)
\(\displaystyle \frac{\mu_0 \pi a^2 N^2}{b^2}\)
解説
電磁気の基本的な問題です。
ソレノイド内部の磁束密度の大きさ\(B\)
下図のように閉経路を考えます。
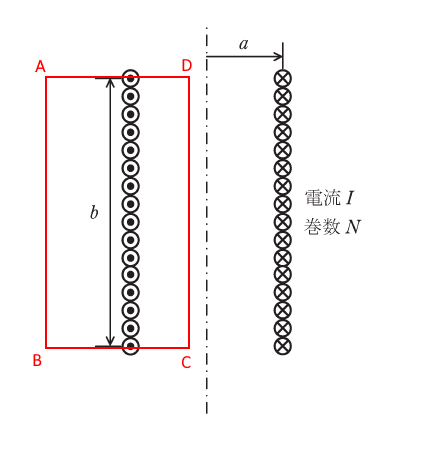
題意より、ソレノイドの外部では磁束密度は0なのでA→Bの経路の磁束密度は0です。
B→CとD→Aは軸に垂直で積分に寄与しません。
ソレノイド内部の磁界の強さを\(H\)とすると、アンペアの周回積分の法則により、\(NI = Hb \)が成立します。よって、\( H = \dfrac{NI}{b} \)であり、これより
\begin{aligned} B &= \mu _0 H \\ &= \dfrac{\mu _0 NI}{b} \\ \end{aligned}
となりますので、答えは(ハ)の\(\displaystyle \frac{\mu_0 NI}{b}\)です。
ソレノイドのインダクタンス\(L \)
\(N\Phi = LI\)より\(L\)を求めます。ここで\(\Phi \)は磁束です。
ソレノイドの断面積を\(S\)とすると、\(BS = \Phi \)であり、\(S = \pi a^2\)なので、
\begin{aligned} LI &= N \Phi \\ &= N B S \\ &= \frac{\mu_0 \pi a^2 N^2 I}{b} \\ L &= \frac{\mu_0 \pi a^2 N^2 }{b} \\ \end{aligned}
よって答えは(ル)の\(\displaystyle \frac{\mu_0 \pi a^2 N^2}{b}\)です。
ソレノイド内部に蓄積された磁界のエネルギー\(W \)
インダクタンスに蓄積されるエネルギーは\( W = \dfrac{1}{2} LI^2 \)なので
\begin{aligned} W &= \dfrac{1}{2} LI^2 \\ &= \dfrac{1}{2} \cdot \frac{\mu_0 \pi a^2 N^2}{b} \cdot I^2 \\ &= \frac{\mu_0 \pi a^2 N^2 I^2}{2b} \\ \end{aligned}
となり、答えは(ヘ)です。
ソレノイドの軸方向に働く力\(F\)
問題にある通り磁界のエネルギーを長さbで偏微分します。
\begin{aligned} F &= \frac{\partial W}{\partial b} \\ &= \frac{\mu_0 \pi a^2 N^2 I^2}{2} \frac{\partial}{\partial b} \left( \frac{1}{b} \right) \\ & = - \frac{\mu_0 \pi a^2 N^2 I^2}{2b^2} \\ & = - \left( \dfrac{\mu_0 N I}{b} \right)^2 \cdot \frac{ \pi a^2 }{2\mu_0} \\ & = - \frac{B^2}{2\mu_0} \times \left( - \pi a^2 \right) \\ \end{aligned}
よって答えは(カ)の\(-\pi a^2\)です。
ソレノイドに働く力の方向
力の方向は長さ\(b\)に対して負の方向に働くのでソレノイドの長さを縮める方向に働きます。
同じ方向に流れる平行電流は引き合うというのは三種でやっていると思いますが、ソレノイドの形から同じ方向の電流が並んでいる(=引き合う)と解釈してもいいかと思います。
- (1)ハ \(\displaystyle \frac{\mu_0 NI}{b}\)
- (2)ル \(\displaystyle \frac{\mu_0 \pi a^2 N^2}{b}\)
- (3)ヘ \(\displaystyle \frac{\mu_0 \pi a^2 N^2 I^2}{2b}\)
- (4)カ \(-\pi a^2\)
- (5)ワ 長さを縮める