電験一種 R1年 理論 問1
次の文章は、真空中のリング状電荷が作る電界に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
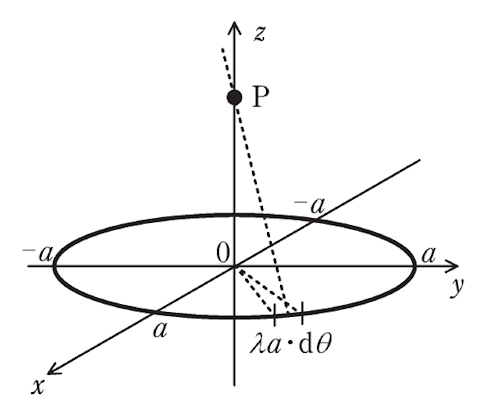
図のように、\(xy\) 平面上に原点を中心とした半径 \(a\) のリング状電荷があり、その線電荷密度は \(\lambda\) である。なお、真空中の誘電率を \(\varepsilon_0\) とする。
リング状電荷の微小角 \(d\theta\) の円弧の電荷 \(\lambda a \cdot d\theta\) により点 \(P(0, 0, z)\) に生じる電界の大きさは (1) である。この電界の \(z\) 方向成分を \(\theta\) について積分することで、リング状電荷全体が点 \(P\) に作る電界の \(z\) 方向成分は (2) と求められる。\(z \geqq 0\) において、その大きさが最も大きい点 \(P\) の \(z\) 座標は (3) である。また、原点の電界は (4) で、無限遠を基準とした原点の電位は (5) である。
| (イ) | \(\displaystyle \frac{\lambda \cdot d\theta}{4\pi\varepsilon_0\sqrt{z^2+a^2}}\) | (ロ) | \(\displaystyle \frac{\lambda z^2}{2\varepsilon_0(z^2+a^2)^{3/2}}\) | (ハ) | \(\displaystyle \frac{\lambda a}{2\varepsilon_0\sqrt{z^2+a^2}}\) |
| (ニ) | \(\displaystyle \frac{\lambda z \cdot d\theta}{4\pi\varepsilon_0(z^2+a^2)}\) | (ホ)(5) | \(\displaystyle \frac{\lambda}{2\varepsilon_0}\) | (ヘ) | \(\displaystyle \frac{\lambda}{2\varepsilon_0 a}\) |
| (ト) | \(\displaystyle \frac{1}{2}a\) | (チ)(2) | \(\displaystyle \frac{\lambda az}{2\varepsilon_0(z^2+a^2)^{3/2}}\) | (リ)(3) | \(\displaystyle \frac{\sqrt{2}}{2}a\) |
| (ヌ) | \(\displaystyle \frac{\lambda}{4\varepsilon_0}\) | (ル) | \(a\) | (ヲ)(4) | \(0\) |
| (ワ)(1) | \(\displaystyle \frac{\lambda a \cdot d\theta}{4\pi\varepsilon_0(z^2+a^2)}\) | (カ) | \(\displaystyle \frac{\sqrt{2}\lambda}{2\varepsilon_0}\) | (ヨ) | \(\displaystyle \frac{\lambda}{4\varepsilon_0 a}\) |
出典:令和1年度第一種電気主任技術者理論科目A問題問1
解説
対称性により電界のz成分以外が0になることを利用して解くのが問題文の誘導からも正しそうですが、それは参考書にもありますので別の解き方でやりたいと思います。実際に問題を解くときは誘導に従った方がいいかと思います。
電界が0でも電位が0ではないっていうのは最初勘違いしてました。電界は電位の勾配なので電位があっても傾きが0なところはあるということですね。
リング状電荷の微小角 \(d\theta\) の円弧の電荷 \(\lambda a \cdot d\theta\) により点 \(P(0, 0, z)\) に生じる電界の大きさ
電荷は\(\lambda a \cdot d\theta\)、点\(P\)までの距離\(r\)は下図のように\(r = \sqrt{z^2+a^2 }\)なので電界の大きさ\(dE\)は
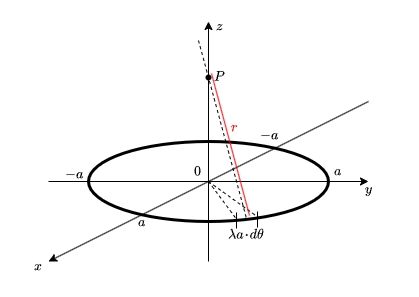
\(\displaystyle dE = \frac{\lambda a \cdot d\theta}{4\pi\varepsilon_0(z^2+a^2)}\)
となります。
リング状電荷全体が点 \(P\) に作る電界の \(z\) 方向成分
誘導のように\(dE\)の\(z\)方向成分を計算してそれを\(\theta\)について積分すればいいですが、ここでは別のやり方でやります。
無限遠点を基準に電荷\(\lambda a \cdot d\theta\)による点 \(P\)の電位を求めます。
\(\displaystyle dV = -\int_{\infty}^{\sqrt{z^2 + a^2}} \frac{\lambda a\cdot d\theta}{4\pi\varepsilon_0 r^2} dr = \frac{\lambda a\cdot d\theta}{4\pi\varepsilon_0 \sqrt{z^2 + a^2}} \)
点\( P \)との距離はリングのどこにおいても\( \sqrt{z^2+a^2 } \)であり、また電位はスカラーなので全体の点\(P\)の電位はこれを\(\theta\)について積分すればよく
\(\displaystyle V = \int_0^{2\pi} dV = \frac{\lambda a}{4\pi\varepsilon_0 \sqrt{a^2 + z^2}} \int_0^{2\pi} d\theta = \frac{\lambda a}{2\varepsilon_0 \sqrt{a^2 + z^2}} \)
となります。\(\vec{E} = -\nabla V \\\)より、\(z\)方向の電界はこれを\(z\)で偏微分したものになるので
\begin{aligned} E_z &= -\frac{\partial V}{\partial z} \\ &= -\frac{\partial}{\partial z} \left( \frac{\lambda a}{2\varepsilon_0 \sqrt{a^2 + z^2}} \right)\\ &= -\frac{\lambda a}{2\varepsilon_0} \frac{\partial}{\partial z} (a^2 + z^2)^{-1/2}\\ &= -\frac{\lambda a}{2\varepsilon_0} \left( -\frac{1}{2} \right) (a^2 + z^2)^{-3/2} (2z)\\ &= \frac{\lambda a z}{2\varepsilon_0 (a^2 + z^2)^{3/2}}\\ \end{aligned}
となり、答えと同じになりました。
\(z \geqq 0\) において\( E_z \)が最も大きい点\(P\)の\(z\)座標
\( E_z \)を\(z\)で微分してそれが0になるところの\(z\)を求めます。
\begin{aligned} \frac{dE_z}{dz} &= \frac{\lambda a}{2\varepsilon_0} \frac{d}{dz} \left\{ \frac{z}{(a^2 + z^2)^{3/2}} \right\} \\ &= \frac{\lambda a}{2\varepsilon_0} \frac{(a^2 + z^2)^{3/2} - z \cdot \frac{3}{2}(a^2 + z^2)^{1/2} \cdot 2z}{(a^2 + z^2)^3}\\ &= \frac{\lambda a}{2\varepsilon_0} \frac{(a^2 + z^2)^{3/2} - 3z^2 (a^2 + z^2)^{1/2}}{(a^2 + z^2)^3}\\ &= \frac{\lambda a}{2\varepsilon_0} \frac{(a^2 + z^2)^{1/2} (a^2 + z^2 - 3z^2)}{(a^2 + z^2)^3}\\ &= \frac{\lambda a}{2\varepsilon_0} \frac{a^2 - 2z^2}{(a^2 + z^2)^{5/2}} \end{aligned}
よって
\begin{aligned} 0 &= a^2 - 2z^2\\ z^2 &= \frac{a^2}{2}\\ z &= \frac{\sqrt{2}}{2}a \quad (z \geqq 0) \end{aligned}
原点の電界
\(\displaystyle E_z = \frac{\lambda a z}{2\varepsilon_0 (a^2 + z^2)^{3/2}} \)に\(z=0 \)代入で0と参考書にありましたが、問題は\(E_z\)だけを聞いているわけではないので\(E_x\)と\(E_y\)が0かも確認した方がいいんじゃないかなと思います。対称性により0ではあるのですが。
(2)の時と同様にまずは原点の電位を出してみたいと思います。積分範囲は\(\infty~a\)になるので
\begin{aligned} dV_0 &= -\int_{\infty}^{a} \frac{\lambda a\cdot d\theta}{4\pi\varepsilon_0 r^2} dr = \frac{\lambda a\cdot d\theta}{4\pi\varepsilon_0 a}\\ &= \frac{\lambda \cdot d\theta}{4\pi\varepsilon_0 } \end{aligned}
となり、これを\(0~2\pi\)で積分すると
\begin{aligned} V_0 &= \int_0^{2\pi} \frac{\lambda}{4\pi\varepsilon_0}d\theta \\ &=\frac{\lambda}{4\pi\varepsilon_0} \cdot 2\pi \\ &= \frac{\lambda}{2\varepsilon_0} \end{aligned}
よって、\(\vec{E} = -\nabla V \\\)より、偏微分するとどこの成分も0になりますので原点の電界は0です。
無限遠を基準とした原点の電位
(4)で求めた通り、\(\displaystyle \frac{\lambda}{2\varepsilon_0}\)です。
参考:\(E_x\)と\(E_y\)が0になることについて
対称性により0になりますと言われても、感覚的にはそうですが本当にそうなのか気になったので計算してみます。
\begin{aligned} dE_x = dE \frac{-a\cos\theta}{\sqrt{a^2 + z^2}} = -\frac{1}{4\pi\varepsilon_0} \frac{\lambda a^2 \cos\theta \cdot d\theta}{(a^2 + z^2)^{3/2}} \\ dE_y = dE \frac{-a\sin\theta}{\sqrt{a^2 + z^2}} = -\frac{1}{4\pi\varepsilon_0} \frac{\lambda a^2 \sin\theta \cdot d\theta}{(a^2 + z^2)^{3/2}} \end{aligned}
\(\displaystyle \frac{a}{\sqrt{a^2 + z^2}} \)は\(dE\)のxy平面に対する成分ということです。\(-\cos\theta\)と\(-\sin\theta\)とは下の図の通りです。
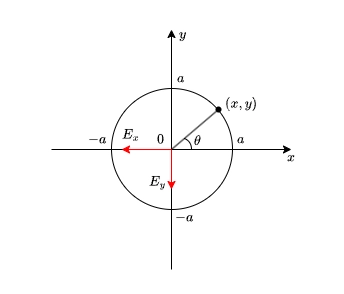
これを1周積分した結果はともに0になります。
\begin{aligned} \int_0^{2\pi} \cos\theta \, d\theta &= [\sin\theta]_0^{2\pi} = \sin(2\pi) - \sin(0) = 0\\ \int_0^{2\pi} \sin\theta \, d\theta &= [-\cos\theta]_0^{2\pi} = -\cos(2\pi) - (-\cos(0)) = -1 + 1 = 0 \end{aligned}
よって\(E_x\)と\(E_y\)は0です。
- (1)ワ \(\displaystyle \frac{\lambda a \cdot d\theta}{4\pi\varepsilon_0(z^2+a^2)}\)
- (2)チ \(\displaystyle \frac{\lambda az}{2\varepsilon_0(z^2+a^2)^{3/2}}\)
- (3)リ \(\displaystyle \frac{\sqrt{2}}{2}a\)
- (4)ヲ \(0\)
- (5)ホ \(\displaystyle \frac{\lambda}{2\varepsilon_0}\)