電験一種 H30年 理論 問6
問6 次の文章は、平行平板コンデンサに関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
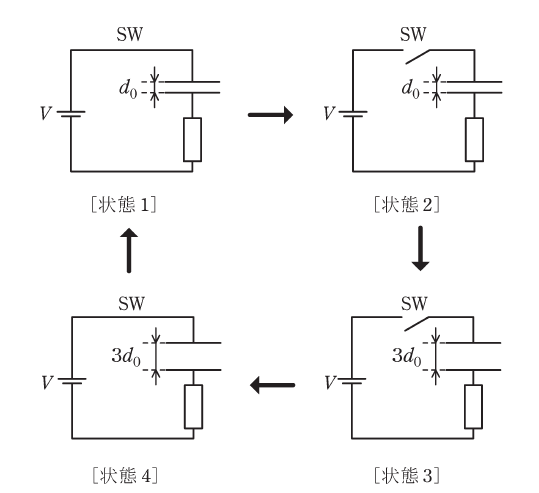
面積\(S\)で同形の導体板2枚からなる平行平板コンデンサが真空中に置かれている。真空の誘電率は\(\varepsilon_0\)である。電極間の距離\(d\)は変更することができる。最初、電極間の距離を\(d=d_0\)とし、図のようにコンデンサ、電圧\(V\)の電源、スイッチSW、負荷抵抗が直列に接続され、SWを閉じて十分な時間が経過している。これを[状態1]としたとき、コンデンサの静電容量は(1)で、そこに蓄えられた電荷は(2)である。
ここで、[状態2]のようにSWを開いて電源を切り離した状態とし、電極に外力を加えながら、電極間の距離をゆっくりと\(d=3d_0\)まで広げ、[状態3]にした。このとき、外力がコンデンサにした仕事量は(3)であり、それがそのままコンデンサにエネルギーとして蓄えられた。
次に、[状態4]のようにSWを閉じて電源を接続すると、電流が流れ、十分な時間が経過するとコンデンサの電圧が電源電圧\(V\)になる。このとき、コンデンサに蓄えられている電荷は(4)で、負荷抵抗で消費したエネルギーは\(\dfrac{2\varepsilon_0 S }{3d_0}V^2\)であった。
最後に、SWを閉じたまま、電極に外力を加えながら、電極間の距離をゆっくりと\(d=d_0\)まで狭め、[状態1]まで戻した。ただし、この操作における電流は極めて小さいため、負荷抵抗における消費電力は無視できるとみなしてよい。\(d=d_0\)に至るまでに電源が供給したエネルギーは(5)である。
[状態1]から[状態2]、[状態3]、[状態4]を経て再び[状態1]に戻す操作を1サイクルと呼ぶ。1サイクルで電源が供給した電荷の合計は0であり、電源が供給したエネルギーは(6)である。よって、このサイクルでは、コンデンサが、機械エネルギーを電気エネルギーに変換して負荷抵抗に供給する発電機の役割をしていることが分かる。
| (イ) | \(\displaystyle \frac{\varepsilon_0 S}{2d_0}\) | (ロ) | \(\displaystyle \frac{\varepsilon_0 S}{2d_0}V^2\) | (ハ) | \(\displaystyle \frac{3\varepsilon_0 S}{2d_0}V^2\) | (ニ)(6) | \(0\) |
| (ホ)(3) | \(\displaystyle \frac{\varepsilon_0 S}{d_0}V^2\) | (ヘ) | \(\displaystyle \frac{\varepsilon_0 S}{6d_0}V^2\) | (ト)(4) | \(\displaystyle \frac{\varepsilon_0 S}{3d_0}V\) | (チ)(2) | \(\displaystyle \frac{\varepsilon_0 S}{d_0}V\) |
| (リ) | \(\displaystyle \frac{\varepsilon_0 S}{6d_0}V\) | (ヌ)(1) | \(\displaystyle \frac{\varepsilon_0 S}{d_0}\) | (ル) | \(\displaystyle \frac{2\varepsilon_0 S}{3d_0}V\) | (ヲ) | \(\displaystyle \frac{2\varepsilon_0 S}{d_0}V\) |
| (ワ) | \(\displaystyle \frac{4\varepsilon_0 S}{3d_0}V^2\) | (カ) | \(\displaystyle \frac{2\varepsilon_0 S}{d_0}\) | (ヨ) | \(\displaystyle \frac{\varepsilon_0 S}{2d_0}V\) | (タ)(5) | \(\displaystyle \frac{2\varepsilon_0 S}{3d_0}V^2\) |
| (レ) | \(\displaystyle \frac{\varepsilon_0 S}{3d_0}V^2\) |
出典:平成30年度第一種電気主任技術者理論科目B問題問6
解説
理論の限られた時間では問題を理解することが難しいかもしれません。
コンデンサの静電容量
電験一種の受験者はこれで躓くことはまずないと思います。
答えは(ヌ)の\(\displaystyle \frac{\varepsilon_0 S}{d_0}\)です。
蓄えられた電荷
\(Q = CV\)より、コンデンサの静電容量は(1)で求めているので
答えは(チ)の\(\displaystyle \frac{\varepsilon_0 S}{d_0}V\)です。
外力がコンデンサにした仕事
電源を切り離した状態としているため、電荷\(Q\)は電極間の距離が変わったとしても変わりません。
この時は静電容量が減る分電圧が上がります。
この時の静電容量を\(C_3\)とすると\(C_3 = \dfrac{\varepsilon_0 S}{3d_0}\)となります。
また、電圧\(V_3\)は\(V_3 = \dfrac{Q}{C_3} = 3V\)となります。静電容量が\(\dfrac{1}{3}\)になった分電圧は3倍になります。
電源が切り離されているため、コンデンサの静電エネルギーの増加分は外力がした仕事量ということになります。
これを計算すると、静電エネルギーの差\(\Delta W\)は
\begin{aligned} \Delta W &= \dfrac{1}{2}\dfrac{\varepsilon_0 S}{3d_0}(3V)^2 - \dfrac{1}{2}\dfrac{\varepsilon_0 S}{d_0}V^2 \\ &= \dfrac{1}{2}\dfrac{3\varepsilon_0 S}{d_0}V^2 - \dfrac{1}{2}\dfrac{\varepsilon_0 S}{d_0}V^2 \\ &= \dfrac{2}{2}\dfrac{\varepsilon_0 S}{d_0}V^2 \\ &= \dfrac{\varepsilon_0 S}{d_0}V^2 \\ \end{aligned}
よって答えは(ホ)の\(\displaystyle \frac{\varepsilon_0 S}{d_0}V^2\)です。
コンデンサに蓄えられている電荷
電源電圧は変わらないので、(2)の\(Q=CV\)と同様に考えると
答えは(ト)の\(\displaystyle \frac{\varepsilon_0 S}{3d_0}V\)となります。
つまり、電源を接続すると静電容量が減った分電荷も減ります。
この時の静電エネルギーの差\(\Delta W_4\)は
\begin{aligned} \Delta W_4 &= \frac{\varepsilon_0 S}{6d_0}V^2 - \frac{3\varepsilon_0 S}{2d_0}V^2 \\ &= -\dfrac{8\varepsilon_0 S}{6d_0}V^2 \\ &= -\dfrac{4\varepsilon_0 S}{3d_0}V^2 \\ \end{aligned}
問題文にある通り、負荷抵抗で\(\dfrac{2\varepsilon_0 S}{3d_0}V^2\)のエネルギーが消費されていますので、残りの\(-\dfrac{2\varepsilon_0 S}{3d_0}V^2\)が電源にいくエネルギーということになります。
\(d=d_0\)に至るまでに電源が供給したエネルギー
おそらくこの問題で一番分かりにくい設問がこれかと思います。
状態4から状態1に戻した時の電荷の変化\(\Delta Q_5\)を計算します。
\begin{aligned} \Delta Q_5 &= \dfrac{\varepsilon_0 S}{d_0}V - \dfrac{\varepsilon_0 S}{3d_0}V \\ &= \dfrac{2\varepsilon_0 S}{3d_0}V \\ \end{aligned}
電源が供給したエネルギー\(U_5\)は、これに電圧\(V\)を乗じたものに等しいので
\begin{aligned} U_5 &= \Delta Q_5 V \\ &= \dfrac{2\varepsilon_0 S}{3d_0}V^2 \\ \end{aligned}
よって答えは(タ)の\(\displaystyle \frac{2\varepsilon_0 S}{3d_0}V^2\)です。
なお、この時の静電エネルギーの変化\(\Delta W_5\)を計算すると
\begin{aligned} \Delta W_5 &= \dfrac{1}{2}\dfrac{\varepsilon_0 S}{d_0}V^2 - \dfrac{1}{6}\dfrac{\varepsilon_0 S}{d_0}V^2 \\ &= \dfrac{1}{3}\dfrac{\varepsilon_0 S}{d_0}V^2 \\ \end{aligned}
となります。問題文より負荷抵抗の消費電力は無視できますが、電源が供給したエネルギーよりコンデンサに蓄えられたエネルギーは少ないです。
電極の間には引き合う力が働いていて、その大きさは\(F= -\dfrac{\partial W}{\partial d} = -\dfrac{\varepsilon_0 S V^2}{2d^2}\)です。
この力は負なので電極間を縮める方向に働いています。
これが\(d=3d_0\)から\(d=d_0\)までに縮めるまでに必要な仕事\(U\)は、
\begin{aligned} U &= \int_{3d_0}^{d_0} F dx \\ &= \int_{3d_0}^{d_0} -\dfrac{\varepsilon_0 S V^2}{2x^2} dx \\ &= \dfrac{\varepsilon_0 S V^2}{2} \left[ \dfrac{1}{x} \right]_{3d_0}^{d_0} \\ &= \dfrac{1}{2} \varepsilon_0 S V^2 \left( \dfrac{1}{d_0} - \dfrac{1}{3d_0} \right)\\ &= \dfrac{1}{2} \varepsilon_0 S V^2 \left( \dfrac{2}{3d_0} \right) \\ &= \dfrac{1}{3}\dfrac{\varepsilon_0 S}{d_0}V^2 \\ \end{aligned}
これは電源から供給されたエネルギーとコンデンサに蓄えられたエネルギーの差に等しいです。
外力が加えられていてもコンデンサが縮むためには機械的エネルギーを消費します。
ここらへんが気になるのであれはもっと専門的な説明を読んでください。(自分にはそこまでの知識がないため)
試験的には、電源から供給されるエネルギーとコンデンサに蓄えられるエネルギーの差は等しくないということだけ覚えておけば他の問題にも応用できるかと思います。
1サイクルで電源が供給したエネルギー
1サイクルで電源が供給した電荷の合計は0とあるところで分かるかと思いますが、答えは(ニ)の\(0\)です。
(5)で\(\displaystyle \frac{2\varepsilon_0 S}{3d_0}V^2\)のエネルギーを電源が供給しており、(4)で\(\dfrac{2\varepsilon_0 S}{3d_0}V^2\)のエネルギーを受け取っていますので電源が供給したエネルギーは差し引き0ということになります。
また、(3)より外力がコンデンサにした仕事量は\(\displaystyle \frac{\varepsilon_0 S}{d_0}V^2\)です。問題より、このうち\(\dfrac{2\varepsilon_0 S}{3d_0}V^2\)は負荷抵抗で消費されていて、\(\dfrac{\varepsilon_0 S}{3d_0}V^2\)はコンデンサを縮めるために消費されています。
エネルギーの収支があっていることが分かります。
なお、最初の充電はサイクルとは別なので、ここでのエネルギーは設問とは関係ありません。
- (1)ヌ \(\displaystyle \frac{\varepsilon_0 S}{d_0}\)
- (2)チ \(\displaystyle \frac{\varepsilon_0 S}{d_0}V\)
- (3)ホ \(\displaystyle \frac{\varepsilon_0 S}{d_0}V^2\)
- (4)ト \(\displaystyle \frac{\varepsilon_0 S}{3d_0}V\)
- (5)タ \(\displaystyle \frac{2\varepsilon_0 S}{3d_0}V^2\)
- (5)ニ \(0\)