電験一種 H30年 理論 問5
次の文章は、直流電圧源に接続された2端子対抵抗回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
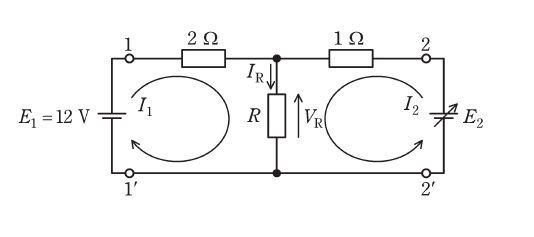
図のように未知抵抗\(R\)を含む2端子対抵抗回路の端子対1-1'に直流電圧源\(E_1\)を接続し、端子対2-2'に可変直流電圧源\(E_2\)を接続した。図の回路の抵抗で消費される電力を\(P\)とする。
図のように閉路電流\(I_1\), \(I_2\)を定めると、閉路方程式は、
\(\begin{bmatrix} E_1 \\ E_2 \end{bmatrix} = \)(1)\( \begin{bmatrix} I_1 \\ I_2 \end{bmatrix}\)
となる。(1)の行列は図の2端子対抵抗回路のZ行列と一致する。
\(E_1 = 12\) Vとし、可変直流電圧源の電圧\(E_2\)を変化させると以下の結果が得られた。
(a) \(E_2 = 15\) Vのとき、\(I_1\)は零となった。
(b) \(E_2 = 8\) Vのとき、\(P\)は最小値24Wとなった。
(c) \(E_2\)を8Vより小さなある値にすると、\(I_R = 1\)Aとなった。
(a)のときの電流\(I_2\)は、\(V_R = E_1\)であるから\(I_2 = \)(2)Aとなる。また、未知抵抗\(R\)の値は\(R = \)(3)Ωとなる。
(b)のときの電流\(I_1\), \(I_2\)は、閉路方程式と\(R = \)(3)Ωより、
\(\begin{bmatrix} I_1 \\ I_2 \end{bmatrix} = \)(4)A
となる。
(c)のときの\(E_2\)は、\(V_R\), \(I_1\)及び\(I_2\)を計算すると、\(E_2 = \)(5)Vとなる。このときの消費電力\(P\)を計算すると、(a)と同じ値になることが分かる。
| (イ) | \(2\) | (ロ) | \(\begin{bmatrix} 2+R & R \\ -R & 1+R \end{bmatrix}\) | (ハ) | \(\begin{bmatrix} 3 \\ -1.5 \end{bmatrix}\) | (ニ) | \(\begin{bmatrix} 1 \\ 1.5 \end{bmatrix}\) |
| (ホ) | \(-3\) | (ヘ)(1) | \(\begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix}\) | (ト)(3) | \(4\) | (チ) | \(6\) |
| (リ)(5) | \(1\) | (ヌ) | \(5\) | (ル)(4) | \(\begin{bmatrix} 2 \\ 0 \end{bmatrix}\) | (ヲ) | \(\begin{bmatrix} 2+R & -R \\ -R & 1+R \end{bmatrix}\) |
| (ワ)(2) | \(3\) | (カ) | \(-2\) | (ヨ) | \(-1\) |
出典:平成30年度第一種電気主任技術者理論科目B問題問5
解説
行列式にさえ慣れていれば特段難しい問題ではないかと思います。
閉路方程式の行列
各閉路の電圧方程式を立てます。
抵抗\(R\)に、\(I_R = I_1 + I_2\) が流れることを考慮すると、左の閉路は
\begin{aligned} E_1 &= 2I_1 + RI_1 + RI_2 \\ &= (2+R)I_1 + RI_2 \\ \end{aligned}
となります。また、右の閉路は
\begin{aligned} E_2 &=I_2 + RI_1 + RI_2 \\ &= RI_1 + (1+R)I_2 \\ \end{aligned}
となります。これらを行列式で表現すると
\begin{aligned} \begin{bmatrix} E_1 \\ E_2 \end{bmatrix} &= \begin{bmatrix} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \\ &= \begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \\ \end{aligned}
となりますので、答えは(ヘ)の\(\begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix}\)です。
\(I_2\)の値
(1)で求めた式に\(E_1=12\)と(a)の条件である\(I_1=0\)と\(E_2=15\)を代入します。
\begin{aligned} E_1 &= (2+R)I_1 + RI_2 \\ E_2 &= RI_1 + (1+R)I_2 \\ 12 &= RI_2 \\ 15 &= (1+R)I_2 \\ \end{aligned}
上記の式より\(R\)を消去します。\(R = \dfrac{12}{I_2}\)なので
\begin{aligned} 15 &= \left(1 + \dfrac{12}{I_2}\right)I_2 \\ 15 &= I_2 + 12 \\ I_2 &= 3 \\ \end{aligned}
よって答えは(ワ)の\(3\)です。
未知抵抗\(R\)の値
(2)で\(I_2\)が3Aと分かっていますので、\(R = \dfrac{12}{I_2}\)より\(R\)は4Ωです。
よって答えは(ト)の\(4\)です。
(b)のときの電流\(I_1\)、\(I_2\)
\(E_1=12\)、\(E_1=8\)、(3)で求めた\(R=4\)を行列式に代入します。
\begin{aligned} \begin{bmatrix} E_1 \\ E_2 \end{bmatrix} &= \begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \\ \begin{bmatrix} 12 \\ 8 \end{bmatrix} &= \begin{bmatrix} 6 & 4 \\ 4 & 5 \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \\ \end{aligned}
よって、以下が成り立ちます。
\begin{aligned} 12 &= 6I_1 + 4I_2 \\ 8 &= 4I_1 + 5I_2 \\ \end{aligned}
この連立方程式を解けばいいのですが、\(P\)を無視していいのか気になるので念のためそちらも計算します。
この回路は抵抗のみなので消費電力は電圧と電流のみで分かります。
\begin{aligned} P &= E_1 I_1 + E_2 I_2 \\ 24 &= 12I_1 + 8I_2 \\ 12 &= 6I_1 + 4I_2 \\ \end{aligned}
\(E_1\)の式と同じ形になりました。連立方程式を解くだけでいいことが分かったので、連立方程式を解きます。
\begin{aligned} 24 &= 12I_1 + 8I_2 \\ 24 &= 12I_1 + 15I_2 \\ 0 &= -7I_2 \\ \end{aligned}
\(I_2=0\)が分かりましたので、これを使用して\(I_1\)を求めると\(I_1=2\)となります。
よって答えは(ル)の\(\begin{bmatrix} 2 \\ 0 \end{bmatrix}\)です。
(c)のときの\(E_2\)
この場合の行列式は以下のようになります。
\begin{aligned} \begin{bmatrix} 12 \\ E_2 \end{bmatrix} &= \begin{bmatrix} 6 & 4 \\ 4 & 5 \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \\ \end{aligned}
また、条件より\(I_1 + I_2=1 \)です。
これらを用いて\(E_1\)を求めます。
\begin{eqnarray} \left\{ \begin{array}{l} 12 &= 6I_1 + 4I_2 \\ E_2 &= 4I_1 + 5I_2 \\ \end{array} \right. \end{eqnarray} \begin{eqnarray} \left\{ \begin{array}{l} 12 &= 6(1-I_2) + 4I_2 \\ E_2 &= 4(1-I_2) + 5I_2 \\ \end{array} \right. \end{eqnarray} \begin{eqnarray} \left\{ \begin{array}{l} 12 &= 6 - 2I_2 \\ E_2 &= 4 + 1I_2 \\ \end{array} \right. \end{eqnarray} \begin{eqnarray} \left\{ \begin{array}{l} 12 &= 6 - 2I_2 \\ 2E_2 &= 8 + 2I_2 \\ \end{array} \right. \end{eqnarray} \begin{aligned} 2E_2 + 12 &= 14 \\ E_2 &= 1 \\ \end{aligned}
よって答えは(リ)の\(1\)です。
- (1)ヘ \(\begin{bmatrix} 2+R & R \\ R & 1+R \end{bmatrix}\)
- (2)ワ \(3\)
- (3)ト \(4\)
- (4)ル \(\begin{bmatrix} 2 \\ 0 \end{bmatrix}\)
- (5)リ \(1\)