電験一種 H30年 理論 問4
次の文章は、真空中の電界下で運動する単一電子による電流に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。なお、電子の質量を\(m\)、電荷量を\(-e\) (\(e \gt 0\)) とする。
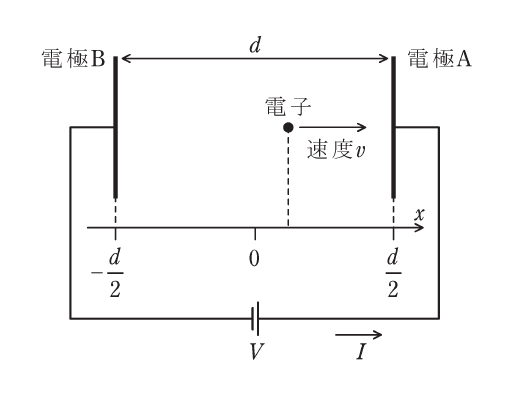
図のように、間隔\(d\)で配置した平行板電極A, B間に一定の電圧\(V\) (\(V \gt 0\)とする) が印加されている。また、電極に垂直な座標軸\(x\)を図に示す方向に定め、電極間の中点を\(x=0\)と定める。ただし、電極間に生じる電界は電極に垂直で一様とみなしてよい。時刻\(t=0\)において、一個の電子が位置\(x=0\)に静止しているものとする。時刻\(t \gt 0\)における電子の位置を\(x\) (\(x \lt \dfrac{d}{2}\)) とし、電界から受ける力を\(d\)、\(V\)等で表すと、ニュートンの運動方程式から微分方程式\(\dfrac{d^2x}{dt^2} = \)(1)が得られる。初期条件を用いてこれを解くことにより、電子の速度\(v = \dfrac{dx}{dt}\)は、時間\(t\)の関数として\(v = \)(2)と表され、位置\(x\)の関数として\(v = \)(3)と表される。
電子が速度\(v\)で運動しているとき、微小時間\(\Delta t\)の間に電界から得るエネルギーは、電子が電界から受けている力と\(\Delta t\)の間に移動する距離とを乗じて、(4)である。一方、このエネルギーは、電圧\(V\)の直流電源から微小時間\(\Delta t\)の間に電流\(I\)が流れ出ることにより供給されることから、電流\(I\)を\(d\)、\(v\)等で表すと(5)と表される。
| (イ) | \(\displaystyle \frac{V}{m_0d}\sqrt{2ex}\) | (ロ) | \(\displaystyle \frac{2eV}{m_0d}\) | (ハ) | \(eVv\Delta t\) | (ニ)(1) | \(\displaystyle \frac{eV}{m_0d}\) |
| (ホ) | \(\displaystyle \frac{e}{dv}\) | (ヘ) | \(\displaystyle \frac{V}{d} \sqrt{\frac{2e}{m_0}x}\) | (ト)(5) | \(\displaystyle \frac{e}{d}v\) | (チ)(4) | \(\displaystyle \frac{eV}{d}v\Delta t\) |
| (リ) | \(\displaystyle \frac{V}{m_0d}t\) | (ヌ) | \(\displaystyle \frac{2eV}{m_0d}\) | (ル)(2) | \(\displaystyle \frac{eV}{m_0d}t\) | (ヲ) | \(\displaystyle \frac{eV}{d}\Delta t\) |
| (ワ)(3) | \(\displaystyle \sqrt{\frac{2eV}{m_0d}x}\) | (カ) | \(\displaystyle \frac{ed}{v}\) | (ヨ) | \(\displaystyle \frac{eV}{2m_0d}\) |
出典:平成30年度第一種電気主任技術者理論科目A問題問4
解説
出題されやすい形式の問題のためよく理解しておく必要があると思います。基本的には誘導に従えば解けます。
ニュートンの運動方程式から得られる微分方程式
電極間の電界\(E\)は一様とみなせると問題文にあるため電界の大きさは、
\[E = \dfrac{V}{d}\]
です。
電子が電界\(E\)から受ける力\(F\)は、
\begin{aligned} F &= e E \\ &= e \dfrac{V}{d}\\ \end{aligned}
で表されます。
また、電子の質量を\(m_0\)、加速度を\(a = \dfrac{d^2x}{dt^2}\) とすると、ニュートンの運動方程式は
\begin{aligned} F &= m_0a \\ &= m_0\dfrac{d^2x}{dt^2}\\ \end{aligned}
で表されます。
これらの力\(F\)は等しいため、等式を立て整理すると
\begin{aligned} m_0\dfrac{d^2x}{dt^2} &= \dfrac{eV}{d} \\ \dfrac{d^2x}{dt^2} &= \dfrac{eV}{m_0d}\\ \end{aligned}
よって答えは(ニ)の\(\displaystyle \frac{eV}{m_0d}\)です。
電子の速度\(v\)
\(v = \dfrac{dx}{dt}\)であることから、(1)の答えを時間\(t\)で積分して\(v\)を求めます。
\begin{aligned} \int \left( \dfrac{d^2x}{dt^2} \right) dt &= \int \dfrac{eV}{m_0d} dt \\ \dfrac{dx}{dt} &= \dfrac{eV}{m_0d} t + C \quad (Cは積分定数)\\ \end{aligned}
問題文より、時刻\(t=0\)において\(x=0\)なので、この時電子の速度\(v\)は\(0\)であることが分かります。
そのため積分定数\(C=0\)です。よって
\begin{aligned} v &= \dfrac{dx}{dt} \\ &= \dfrac{eV}{m_0d} t \\ \end{aligned}
となり、答えは(ル)の\(\displaystyle \frac{eV}{m_0d}t\)です。
位置\(x\)の関数として表した速度\(v\)
速度を時間で積分すると距離になるので、(2)の答えを\(t\)で積分します。
\begin{aligned} x &= \int v dt \\ &= \int \dfrac{eV}{m_0d}t dt \\ &= \dfrac{1}{2}\dfrac{eV}{m_0d}t^2 + C_1 \quad (C_1は積分定数) \\ \end{aligned}
\(t=0\)のとき、\(x=0\)なので、積分定数\(C_1\)は0です。よって\(x = \dfrac{1}{2}\dfrac{eV}{m_0d}t^2 \)となります。
これを\(t\)について整理しますと、
\begin{aligned} x &= \dfrac{1}{2}\dfrac{eV}{m_0d}t^2 \\ t^2 &= \dfrac{2m_0d}{eV}x \\ t &= \sqrt{\dfrac{2m_0d}{eV}x} \\ \end{aligned}
となります。これを\(v\)の式に代入します。
\begin{aligned} v &= \dfrac{eV}{m_0d} t \\ &= \dfrac{eV}{m_0d} \cdot \sqrt{\dfrac{2m_0d}{eV}x}\\ &= \sqrt{\dfrac{2eV}{m_0d}x}\\ \end{aligned}
よって答えは(ワ)の\(\displaystyle \sqrt{\frac{2eV}{m_0d}x}\)です。
微小時間\(\Delta t\)の間に電界から得るエネルギー
電子が電界から得るエネルギーは、電界が電子にする仕事に等しく、「力 × 移動距離」です
(1)より、電子が電界から受ける力\(F\)の大きさは、\(\dfrac{eV}{d}\)です。
また、電子が速度\(v\)で運動しているとき、微小時間\(\Delta t\)の間に移動する距離\(\Delta x\)は、\(\Delta x = v \Delta t\)です。
電子が電界から得るエネルギー\(\Delta W\)は、力\(F\)と移動距離\(\Delta x\)の積で表されます。よって、
\begin{aligned} \Delta W &= F \cdot \Delta x \\ &= \left(\dfrac{eV}{d}\right) \cdot (v \Delta t) \\ &= \dfrac{eV}{d}v\Delta t \\ \end{aligned}
となり、答えは(チ)の\(\displaystyle \frac{eV}{d}v\Delta t\)です。
電流\(I\)を\(d\)、\(v\)等で表す
電圧\(V\)の直流電源から微小時間\(\Delta t\)の間に電流\(I\)が流れ出ることにより供給されるエネルギーは、\(P \Delta t = V I \Delta t\)です。
また、(4)で、電子が電界から得るエネルギーは、\(\Delta W = \dfrac{eV}{d}v\Delta t\)でした。
これらのエネルギーは等しいので、
\begin{aligned} P \Delta t &= \Delta W \\ V I \Delta t &= \dfrac{eV}{d}v\Delta t \\ \end{aligned}
この式から電流\(I\)について解きます。
\begin{aligned} V I \Delta t &= \dfrac{eV}{d}v\Delta t \\ V I &= \dfrac{eV}{d}v \\ I &= \dfrac{e}{d}v \\ \end{aligned}
よって、答えは(ト)の\(\displaystyle \frac{e}{d}v\)です。
- (1)ニ \(\displaystyle \frac{eV}{m_0d}\)
- (2)ル \(\displaystyle \frac{eV}{m_0d}t\)
- (3)ワ \(\displaystyle \sqrt{\frac{2eV}{m_0d}x}\)
- (4)チ \(\displaystyle \frac{eV}{d}v\Delta t\)
- (5)ト \(\displaystyle \frac{e}{d}v\)