電験一種 H30年 理論 問3
次の文章は、回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
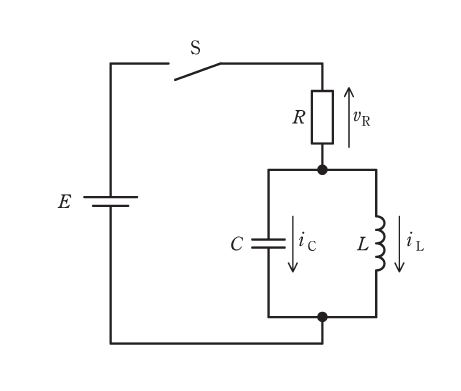
図の回路は、時刻\(t \lt 0\)ではスイッチSは開いており、キャパシタ\(C\)の電荷\(q\)は0である。
時刻\(t = 0\)でスイッチSを閉じると、時刻\(t \geqq 0\)では電圧に関する以下の二つの微分方程式
\(L\dfrac{di_L}{dt} + \)(1)\( = E \quad \cdots \text{①}\)
\(L\dfrac{di_L}{dt} - \)(2)\( = 0 \quad \cdots \text{②}\)
が成立する。
上記の①式及び②式から、インダクタ\(L\)の電流\(i_L\)に関する微分方程式
(3)\( + L\dfrac{di_L}{dt} + Ri_L = E\)
を得る。
したがって、抵抗\(R\)の電圧\(v_R\)が振動的となる条件は、
(4)\( \lt 0\)
で与えられる。
また、スイッチSを閉じて十分時間が経過し、回路が定常状態になった時のキャパシタ\(C\)の電荷は、
\(q = \)(5)
となる。
| (イ) | \(\displaystyle \frac{1}{2}CE^2\) | (ロ) | \(CE\) | (ハ)(1) | \(R(i_L+i_C)\) | (ニ)(4) | \(L-4R^2C\) |
| (ホ) | \(Ri_L\) | (ヘ) | \(Ri_C\) | (ト) | \(\displaystyle \frac{1}{RC}\int i_C dt\) | (チ)(5) | \(0\) |
| (リ)(3) | \(RLC\displaystyle \frac{d^2 i_L}{dt^2}\) | (ヌ) | \(\displaystyle \int i_C dt\) | (ル) | \(4R^2C - L\) | (ヲ) | \(LC\displaystyle \frac{d^2 i_L}{dt^2}\) |
| (ワ) | \(4R^2C + L\) | (カ)(2) | \(\displaystyle \frac{1}{C}\int i_C dt\) | (ヨ) | \(RC\displaystyle \frac{d^2 i_L}{dt^2}\) |
出典:平成30年度第一種電気主任技術者理論科目A問題問3
解説
過渡現象の問題は出題されやすく、かつ解きやすいため得点源となるのでよく理解する必要があると思います。
一つ目の微分方程式
電源と抵抗を含む方の微分方程式です。
抵抗\(R\)に流れる電流は\(i_L+i_C\)になることに注意して回路方程式を立てると
\[L\dfrac{di_L}{dt} + R(i_L + i_C) = E\]
となり、答えは(ハ)の\(R(i_L+i_C)\)です。
二つ目の微分方程式
キャパシタ\(C\)とインダクタ\(L\)の閉回路の微分方程式です。
キャパシタにかかる電圧の計算方法が分かれば間違えないかと思います。
なお、電流の向きの定義により符号にマイナスがつきます。
\[L\dfrac{di_L}{dt} - \dfrac{1}{C}\int i_C dt = 0\]
答えは(カ)の\(\displaystyle \frac{1}{C}\int i_C dt\)です。
インダクタ\(L\)の電流\(i_L\)に関する微分方程式
(1)で求めた下記式より電流\(i_C\)を消去することを目指します。
\[L\dfrac{di_L}{dt} + R(i_L + i_C) = E\]
(2)で求めた式を時間\(t\)で微分して、\(i_C\)について整理します。
\begin{aligned} L\dfrac{di^2_L}{dt^2} - \dfrac{1}{C} i_C &= 0 \\ i_C &= CL\dfrac{di^2_L}{dt^2} \\ \end{aligned}
(1)で求めた式に(2)で求めた式を代入して整理します。
\begin{aligned} L\dfrac{di_L}{dt} + R(i_L + i_C) &= E \\ L\dfrac{di_L}{dt} + R(i_L + CL\dfrac{di^2_L}{dt^2}) &= E \\ RLC\dfrac{d^2 i_L}{dt^2} + L\dfrac{di_L}{dt} + Ri_L &= E \\ \end{aligned}
よって答えは(リ)の\(RLC\displaystyle \frac{d^2 i_L}{dt^2}\)です。
抵抗\(R\)の電圧\(v_R\)が振動的となる条件
抵抗\(R\)の電圧\(v_R\)は\(v_R = R(i_L+i_C)\)で表されるため、電圧\(v_R\)が振動的となる条件は(3)のインダクタ\(L\)の電流\(i_L\)に関する微分方程式が振動解を持つ条件を調べることで判断できます。
(3)で得られた微分方程式は以下の通りです。
\begin{aligned} RLC\dfrac{d^2 i_L}{dt^2} + L\dfrac{di_L}{dt} + Ri_L &= E \\ \end{aligned}
この種の微分方程式の過渡応答は、特性方程式の根の性質によって決まります。特性方程式は、各項の微分次数を対応するべき乗に置き換えることで得られます。
\[RLC\lambda^2 + L\lambda + R = 0\]
この2次方程式の根\(\lambda\)を解の公式を用いて求めます。
\[\lambda = \dfrac{-L \pm \sqrt{L^2 - 4R^2LC}}{2RLC}\]
過渡応答が振動的となる条件は、特性方程式の根が共役な複素数となる場合です。
これは根号の中の判別式が負になる場合に相当します。この時は電流に三角関数がでてきます。
したがって振動的となる条件は \(L^2 - 4R^2LC < 0\) です。
両辺を\(L\)で割り、問題で示された形となるように整理します。(\(L > 0\)なので不等号の向きは変わりません)。
\[ L - 4R^2C < 0 \]
よって答えは(ニ)の\(L-4R^2C\)です。
スイッチSを閉じて十分時間が経過し、回路が定常状態になった時のキャパシタ\(C\)の電荷
定常状態において、インダクタ\(L\)は短絡状態とみなせます。
この時インダクタ\(L\)の電圧は0なので、並列であるキャパシタ\(C\)の電圧も0です。
よって電荷\(q\)は0となり、答えは(チ)です。
- (1)ハ \(R(i_L+i_C)\)
- (2)カ \(\displaystyle \frac{1}{C}\int i_C dt\)
- (3)リ \(RLC\displaystyle \frac{d^2 i_L}{dt^2}\)
- (4)ニ \(L-4R^2C\)
- (5)チ \(0\)