電験一種 H30年 理論 問2
次の文章は、非対称三相起電力を平衡三相負荷に接続した回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。ただし、電圧、電流及びアドミタンスの単位は、それぞれ[V], [A]及び[S]とする。
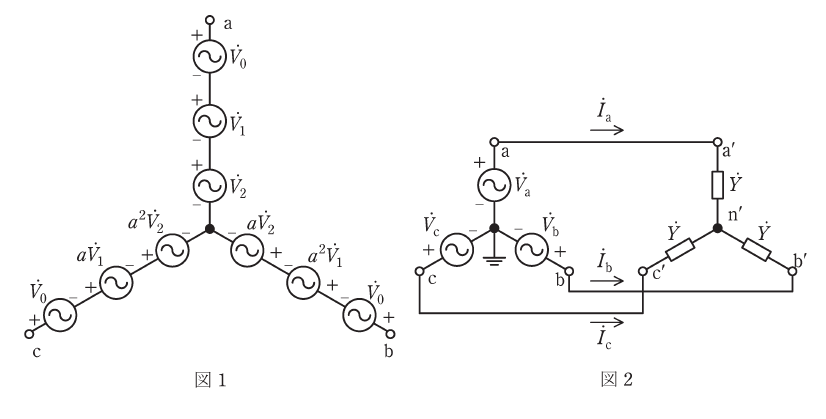
一般に非対称三相起電力\((\dot{V}_a, \dot{V}_b, \dot{V}_c)\)は図1に示すように対称三相起電力\((\dot{V}_0, \dot{V}_1, \dot{V}_2)\)を用いて表すことができる。ここで\(\dot{V}_0, \dot{V}_1, \dot{V}_2\)は\(\dot{V}_a, \dot{V}_b, \dot{V}_c\)から、
\(\begin{pmatrix} \dot{V}_0 \\ \dot{V}_1 \\ \dot{V}_2 \end{pmatrix} = \dfrac{1}{3} \begin{pmatrix} 1 & 1 & 1 \\ 1 & a & a^2 \\ 1 & a^2 & a \end{pmatrix} \begin{pmatrix} \dot{V}_a \\ \dot{V}_b \\ \dot{V}_c \end{pmatrix}\)
で導かれる。ただし、\(a = e^{j\frac{2\pi}{3}}\)である。
図2に示す非対称三相起電力\((\dot{V}_a, \dot{V}_b, \dot{V}_c)\)に\(\dot{Y} = \dfrac{1}{10}\)の平衡三相負荷を接続した回路を考える。\(\dot{V}_a = 100\), \(\dot{V}_b = 80a^2\), \(\dot{V}_c = 120a\)のとき、\(\dot{V}_0\), \(\dot{V}_1\), \(\dot{V}_2\)はそれぞれ、
\(\dot{V}_0 = \)(1), \(\dot{V}_1 = \)(2), \(\dot{V}_2 = -j\dfrac{20\sqrt{3}}{3}\)となる。このときの線電流は、零相分\(\dot{V}_0\)と正相分\(\dot{V}_1\)と逆相分\(\dot{V}_2\)の重ね合わせの理を用いることで求めることができる。零相分\(\dot{V}_0\)のみが存在する場合には点a', 点b', 点c'は等電位となるため回路に電流は流れず各線電流は零となる。一方、正相分\(\dot{V}_1\)のみが存在する場合の各線電流は、\(\dot{I}_{a1} = \)(2)\( \dot{Y}\), \(\dot{I}_{b1} = \)(2)\( \dot{Y}a^2\), \(\dot{I}_{c1} = \)(2)\( \dot{Y}a\)となる。同様に、逆相分\(\dot{V}_2\)のみが存在する場合の各線電流は、\(\dot{I}_{a2} = \dot{Y}\dot{V}_2 = -j\dfrac{2\sqrt{3}}{3}\), \(\dot{I}_{b2} = \dot{Y}a\dot{V}_2 = 1+j\dfrac{\sqrt{3}}{3}\), \(\dot{I}_{c2} = \dot{Y}a^2\dot{V}_2 = -1+j\dfrac{\sqrt{3}}{3}\)となる。これより、図2の\(\dot{I}_a\)と\(\dot{I}_b\)は、
\(\dot{I}_a = \dot{I}_{a1} + \dot{I}_{a2} = \)(3)
\(\dot{I}_b = \dot{I}_{b1} + \dot{I}_{b2} = -4-j\dfrac{14\sqrt{3}}{3}\)
と求められる。また、点n'でのキルヒホッフの電流則より、
\(\dot{I}_a + \dot{I}_b + \dot{I}_c = \)(4)であると考慮すると、\(\dot{I}_c = \)(5)が求められる。
| (イ) | \(j20\sqrt{3}\) | (ロ) | \(14+j\displaystyle \frac{16\sqrt{3}}{3}\) | (ハ) | \(10\) | (ニ) | \(-100\) |
| (ホ) | \(100-j\displaystyle \frac{2\sqrt{3}}{3}\) | (ヘ)(3) | \(10-j\displaystyle \frac{2\sqrt{3}}{3}\) | (ト)(2) | \(100\) | (チ) | \(1\) |
| (リ) | \(j\displaystyle \frac{40\sqrt{3}}{3}\) | (ヌ)(1) | \(j\displaystyle \frac{20\sqrt{3}}{3}\) | (ル) | \(300\) | (ヲ)(5) | \(-6+j\displaystyle \frac{16\sqrt{3}}{3}\) |
| (ワ) | \(-6-j\displaystyle \frac{20\sqrt{3}}{3}\) | (カ)(4) | \(0\) | (ヨ) | \(-10-j\displaystyle \frac{2\sqrt{3}}{3}\) |
出典:平成30年度第一種電気主任技術者理論科目A問題問2
解説
一見難しそうですが実際はただのベクトルオペレータを使用した計算です。
零相分電圧\(\dot{V_0}\)
問題文より、非対称三相起電力\((\dot{V}_a, \dot{V}_b, \dot{V}_c)\)を対称座標法によって零相分\(\dot{V}_0\)、正相分\(\dot{V}_1\)、逆相分\(\dot{V}_2\)に変換する式は以下のように与えられています。
\[\begin{pmatrix} \dot{V}_0 \\ \dot{V}_1 \\ \dot{V}_2 \end{pmatrix} = \dfrac{1}{3} \begin{pmatrix} 1 & 1 & 1 \\ 1 & a & a^2 \\ 1 & a^2 & a \end{pmatrix} \begin{pmatrix} \dot{V}_a \\ \dot{V}_b \\ \dot{V}_c \end{pmatrix}\]
ここで、\(a = e^{j\frac{2\pi}{3}}\) です。
求めるのは零相分\(\dot{V}_0\)なので、上記の行列演算の1行目を取り出します。
\[\dot{V}_0 = \dfrac{1}{3} (\dot{V}_a + \dot{V}_b + \dot{V}_c)\]
問題文で与えられた値を基に計算します。
\begin{aligned} \dot{V}_0 &= \dfrac{1}{3} (\dot{V}_a + \dot{V}_b + \dot{V}_c) \\ &= \dfrac{1}{3} (100 + 80a^2 + 120a) \\ &= \dfrac{1}{3} (100 + 80a^2 + 80a + 40a) \\ &= \dfrac{1}{3} \left\{ 100 + 80(a^2 + a) + 40a\right\} \\ &= \dfrac{1}{3} \left\{100 + 80(-1) + 40a\right\} \quad (\because a^2+a+1 = 0) \\ &= \dfrac{1}{3} (100 - 80 + 40a) \\ &= \dfrac{1}{3} (20 + 40a) \\ &= \dfrac{20}{3} (1 + 2a) \\ &= \dfrac{20}{3} \left\{ 1 + 2\left(-\dfrac{1}{2} + j\dfrac{\sqrt{3}}{2}\right)\right\} \\ &= \dfrac{20}{3} (1 - 1 + j\sqrt{3}) \\ &= \dfrac{20}{3} (j\sqrt{3}) \\ &= j\dfrac{20\sqrt{3}}{3} \\ \end{aligned}
よって、答えは(ヌ)の\(j\displaystyle \frac{20\sqrt{3}}{3}\)です。
正相分電圧\(\dot{V_1}\)
(1)と同様に、正相分電圧\(\dot{V_1}\)の式を求めると
\[\dot{V}_1 = \dfrac{1}{3} (\dot{V}_a + a\dot{V}_b + a^2\dot{V}_c)\]
となります。
問題文に与えられた値を代入して計算します。
\begin{aligned} \dot{V}_0 &= \dfrac{1}{3} (\dot{V}_a + a\dot{V}_b + a^2\dot{V}_c) \\ &= \dfrac{1}{3} \left\{100 + a(80a^2) + a^2(120a)\right\} \\ &= \dfrac{1}{3} (100 + 80 + 120) \quad (\because a^3 = 1) \\ &= \dfrac{1}{3} (300) \\ &= 100 \\ \end{aligned}
よって答えは(ト)の\(100\)です。
線電流\(\dot{I_a}\)
(2)の答えと問題で与えられたアドミタンスを使用して\(\dot{I}_{a1}\)を求めます。
\begin{aligned} \dot{I}_{a1} &= \dot{V_1} \dot{Y}\\ &= 100 \cdot \dfrac{1}{10} \\ &= 10 \\ \end{aligned}
逆相分電流\(\dot{I}_{a2}\)は問題で与えられており、\(\dot{I}_{a2} = \dot{Y}\dot{V}_2 = -j\dfrac{2\sqrt{3}}{3}\)です。
重ね合わせの理により、線電流\(\dot{I}_a\)は、正相分電流、逆相分電流の和で表されます。
\begin{aligned} \dot{I}_a &= \dot{I}_{a1} + \dot{I}_{a2} \\ &= 10 - j\dfrac{2\sqrt{3}}{3} \\ \end{aligned}
よって、答えは(ヘ)の\(10-j\displaystyle \frac{2\sqrt{3}}{3}\)です。
\(\dot{I}_a + \dot{I}_b + \dot{I}_c \)
キルヒホッフの電流則は電気回路の任意の節点において、流れ込む電流の総和と流れ出す電流の総和が等しいという法則です。
図の回路においては\(\dot{I}_a\) 、 \(\dot{I}_b\) 、 \(\dot{I}_c \)が流れ出る先はないので3つの電流の和は0になります。
\begin{aligned} \dot{I}_a + \dot{I}_b + \dot{I}_c &= 0 \\ \end{aligned}
よって答えは(カ)の\(0\)です。
線電流\(\dot{I}_c\)
(4)より、線電流\(\dot{I}_c\)は以下で表すことができます。
\begin{aligned} 0 &= \dot{I}_a + \dot{I}_b + \dot{I}_c\\ \dot{I}_c &= -\dot{I}_a - \dot{I}_b \\ \end{aligned}
(3)で求めた\(\dot{I}_a\)と問題文で示されている\(\dot{I}_b\)を用いて計算します。
\begin{aligned} \dot{I}_c &= - \left(10 - j\dfrac{2\sqrt{3}}{3}\right) - \left(-4 - j\dfrac{14\sqrt{3}}{3}\right) \\ &= -6 + j\dfrac{16\sqrt{3}}{3} \\ \end{aligned}
よって、答えは(ヲ)の\(-6+j\displaystyle \frac{16\sqrt{3}}{3}\)です。
- (1)ヌ \(j\displaystyle \frac{20\sqrt{3}}{3}\)
- (2)ト \(100\)
- (3)ヘ \(10-j\displaystyle \frac{2\sqrt{3}}{3}\)
- (4)カ \(0\)
- (5)ヲ \(-6+j\displaystyle \frac{16\sqrt{3}}{3}\)