電験一種 H30年 理論 問1
次の文章は、円電流が作り出す磁束密度に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。なお、\(\mu_0\)は真空の透磁率である。
図1に示すように\(z\)軸を中心軸とし、\(z=\zeta\)の位置に中心をもつ半径\(a\)の円電流\(I\)が原点(\(z\)軸上の\(z=0\)の点)に作る磁束密度をビオ・サバールの法則を用いて求める。円電流上の電流素片\(I ds\)(\(ds\)は円電流に沿った微小区間の長さ)と原点を結んだ直線と\(z\)軸とのなす角度を\(\theta\)とすると、\(\sin \theta = \dfrac{a}{\sqrt{a^2 + \zeta^2}}\)が成立することから、電流素片が原点に作る磁束密度の\(z\)方向の成分は\(\theta\)を用いて、
\(dB_z = \dfrac{\mu_0 I }{4\pi } \dfrac{ \sin^3 \theta}{ a^2}ds\)
と表される。これを円周方向に線積分すると、円電流\(I\)が原点に作る磁束密度の\(z\)方向成分は、
\(B_z(\theta) = \)(1)
と求められる。一方、原点における磁束密度の\(z\)軸に直交する成分は、対称性から
\(B_\perp(\theta) = \)(2)
となる。
次に、図2に示すように\(z\)軸を中心軸とし、原点を中心とする半径\(a\)、長さ\(2a\)の有限長ソレノイドを考える。\(z=\zeta\)の位置に中心をもつ円電流\(I\)が原点に作る磁束密度の\(z\)方向成分を\(B_z(\zeta)\)と置くと、単位長さ当たりの巻き数\(n\)が十分に大きい場合には、ソレノイドに流れる電流\(I\)がソレノイドの中心に作る磁束密度は、
\(\displaystyle B_1 = \int_{-a}^{a} n B_z(\zeta) d\zeta\)
と表される。いま、ソレノイド上の電流素片と原点を結んだ直線と\(z\)軸とのなす角度を\(\theta\)とすると、\(\zeta = \dfrac{a}{\tan \theta}\)の関係が成り立つので、\(d\zeta = -\dfrac{a}{\sin^2 \theta} d\theta\)を利用して変数変換すると、
\(\displaystyle B_1 = \int_{3\pi/4}^{\pi/4} \)(3)\( d\theta = \)(4)
となる。
同様に、無限長ソレノイドの軸上の磁束密度は、
\(B_2 = \)(5)
と求められる。

| (イ) | \(\mu_0 I\) | (ロ)(1) | \(\displaystyle \frac{\mu_0 I }{2} \frac{\sin^3 \theta}{a} \) | (ハ) | \(\displaystyle \frac{\mu_0 nI}{2}\) | (ニ) | \(2\mu_0 nI\) |
| (ホ)(5) | \(\mu_0 nI\) | (ヘ)(3) | \(-\displaystyle \frac{\mu_0 nI}{2}\sin\theta\) | (ト)(4) | \(\displaystyle \frac{\mu_0 nI}{\sqrt{2}}\) | (チ) | \(-\displaystyle \frac{\mu_0 nI}{2}\) |
| (リ) | \(4\mu_0 nI\) | (ヌ) | \(\sqrt{2}\mu_0 nI\) | (ル) | \(\displaystyle \frac{\mu_0 I }{2} \frac{\sin^2 \theta }{a}\) | (ヲ) | \(\displaystyle \frac{\mu_0 I}{2a}\) |
| (ワ)(2) | \(0\) | (カ) | \(-\mu_0 nI\displaystyle \frac{a}{\sin\theta}\) | (ヨ) | \(\mu_0 I \sin\theta\) |
出典:平成30年度第一種電気主任技術者理論科目A問題問1
解説
誘導に従えば解ける問題ですが、他の問題に応用できるように各式を導出できるようにするべきかと思います。
円電流\(I\)が原点に作る磁束密度の\(z\)方向成分
難しいことが書いてあるように思えますが、実際には問題に\(dB_z\)の計算式が与えられているのでこれを円周方向に線積分するだけです。円の半径が\(a\)なことから、一周は\(2\pi a\)なので
\begin{aligned} B_z(\theta) &= \int_0^{2\pi a} dB_z \\ &= \int_0^{2\pi a} \frac{\mu_0 I }{4\pi} \frac{\sin^3 \theta}{a^2} ds \\ &= \frac{\mu_0 I }{4\pi } \frac{ \sin^3 \theta}{ a^2} \times 2\pi a \\ &= \frac{\mu_0 I }{2 } \frac{ \sin^3 \theta}{a} \\ \end{aligned}
となり、答えは(ロ)の\(\displaystyle \frac{\mu_0 I }{2} \frac{\sin^3 \theta}{a} \)です。
なお、ビオ・サバールの法則で下記のような式を見ることがあるかと思います。
\begin{aligned} dB =\displaystyle \frac{\mu_0 I dl}{4\pi r^2} \sin\theta \\ \end{aligned}
ここの\( \sin \theta \)は導体の微小部分の接線と点Pとの角度であり、今回の\( \sin \theta \)とは別です。
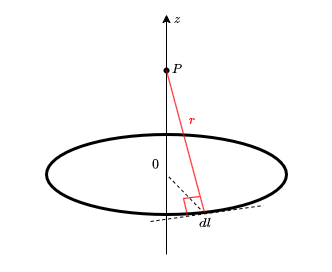
つまり上の図の角度なので、円周上では常に\(\sin \theta = 1\)です。
\(dB_z\)は以下のように導出されます。
下の図より、先ほどの式の\(r = \sqrt{a^2+\zeta^2}\)であり、また\(B_z = B \dfrac{a}{\sqrt{a^2+\zeta^2}} \)なので、
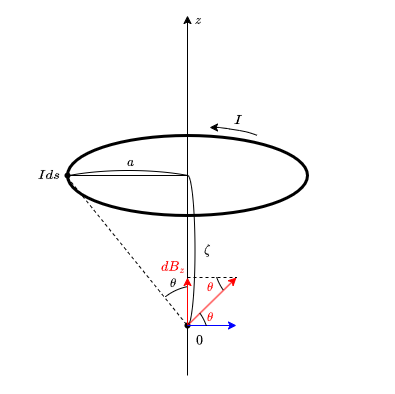
\begin{aligned} dB_z &=\displaystyle \frac{\mu_0 I ds}{4\pi (\sqrt{a^2+\zeta^2})^2} \dfrac{a}{\sqrt{a^2+\zeta^2}} \\ &=\displaystyle \frac{\mu_0 I ds}{4\pi a^2 } \left( \dfrac{a}{\sqrt{a^2+\zeta^2}} \right)^3\\ \end{aligned}
ここで、\(\sin \theta = \dfrac{a}{\sqrt{a^2+\zeta^2}} \)なので
\begin{aligned} dB_z &= \dfrac{\mu_0 I }{4\pi } \dfrac{ \sin^3 \theta}{ a^2}ds \\ \end{aligned}
原点における磁束密度の\(z\)軸に直行する成分
対称性から、というワードで察せるとは思いますが、\(z\)軸に直行する成分は対称性により積分すると0になります。
よって答えは(ワ)の0です。
上の画像で青い線の部分です。
変数変化した後の磁束密度の式
\(d\zeta = -\dfrac{a}{\sin^2 \theta} d\theta\)を使用して変数変換します。
\begin{aligned} B_1 &= \int_{-a}^{a} n B_z(\zeta) d\zeta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} n B_z(\theta) \times \left(-\frac{a}{\sin^2 \theta}\right) d\theta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} n\frac{\mu_0 I}{2} \frac{\sin^3 \theta}{a} \times \left(-\frac{a}{\sin^2 \theta}\right) d\theta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} \left( - \frac{\mu_0 n I}{2} \sin \theta \right) d\theta \\ \end{aligned}
よって答えは(ヘ)の\(-\displaystyle \frac{\mu_0 nI}{2}\sin\theta\)です。
試験でやるべきではないですが、より細かく求めてみます。
前述の式より、\(B_z(\theta)\)ではなく\(B_z(\zeta)\)を求めます。
\begin{aligned} dB_z &=\displaystyle \frac{\mu_0 I ds}{4\pi a^2 } \left( \dfrac{a}{\sqrt{a^2+\zeta^2}} \right)^3\\ &=\displaystyle \frac{\mu_0 I ds}{4\pi } \dfrac{a}{(a^2+\zeta^2)^{\frac{3}{2}}}\\ B_z(\zeta) &= \int_0^{2\pi a} \frac{\mu_0 I }{4\pi } \dfrac{a}{(a^2+\zeta^2)^{\frac{3}{2}}} ds \\ &= \frac{\mu_0 I }{2} \dfrac{a^2}{(a^2+\zeta^2)^{\frac{3}{2}}} \end{aligned}
よって、\(B_1\)は以下となります。
\begin{aligned} B_1 &= \int_{-a}^{a} n B_z(\zeta) d\zeta \\ &= \int_{-a}^{a} n \frac{\mu_0 I}{2} \dfrac{a^2}{(a^2+\zeta^2)^{\frac{3}{2}}} d\zeta \\ \end{aligned}
ここから\(\zeta = \dfrac{a}{\tan\theta}\)とおいて置換積分します。まず\(\zeta\)を\(\theta \)で微分します。
\begin{aligned} \zeta &= \frac{a}{\frac{\sin\theta}{\cos\theta}} = \frac{a\cos\theta}{\sin\theta} \\ \frac{d\zeta}{d\theta} &= \frac{(-a\sin\theta)(\sin\theta) - (a\cos\theta)(\cos\theta)}{\sin^2\theta}\\ &= \frac{-a(\sin^2\theta + \cos^2\theta)}{\sin^2\theta} \\ &= -\frac{a}{\sin^2\theta} \\ \end{aligned}
問題文にある通り、\(d\zeta = -\dfrac{a}{\sin^2\theta} d\theta \)です。
\(B_1\)の式を\(\zeta = \dfrac{a}{\tan\theta}\)とします。
ここで、\(\zeta = -a\)のとき、\( -1 = \dfrac{1}{\tan\theta } \)なので、\(\theta = \dfrac{3\pi}{4} \)です。
同様に、\(\zeta = a\)のときは\(\theta = \dfrac{\pi}{4} \)です。よって
\begin{aligned} B_1 &= \int_{-a}^{a} n \frac{\mu_0 I}{2} \dfrac{a^2}{(a^2+\zeta^2)^{\frac{3}{2}}} d\zeta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} n \frac{\mu_0 I}{2} \dfrac{a^2}{\left\{ a^2+\left( \dfrac{a}{\tan\theta}\right)^2 \right\} ^{\frac{3}{2}}} \left( -\dfrac{a}{\sin^2\theta} \right) d\theta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} n \frac{\mu_0 I}{2} \dfrac{a^2}{a^3 \left\{ 1+\left( \dfrac{1}{\tan\theta}\right)^2 \right\} ^{\frac{3}{2}}} \left( -\dfrac{a}{\sin^2\theta} \right) d\theta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} n \frac{\mu_0 I}{2a} \dfrac{1}{ \left( \dfrac{\sin^2 \theta + \cos^2 \theta}{\sin^2 \theta}\right) ^{\frac{3}{2}}} \left( -\dfrac{a}{\sin^2\theta} \right) d\theta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} n \frac{\mu_0 I}{2a} \sin^3 \theta \left( -\dfrac{a}{\sin^2\theta} \right) d\theta \\ &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} \left( - \frac{\mu_0 n I}{2} \sin \theta \right) d\theta \\ \end{aligned}
となります。
変数変化した後の磁束密度の式の答え
先ほどの\(B_1\)の式の答えを求めます。
\begin{aligned} B_1 &= \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} \left( - \frac{\mu_0 n I}{2} \sin \theta \right) d\theta \\ &= -\frac{\mu_0 nI}{2} \int_{\frac{3\pi}{4}}^{\frac{\pi}{4}} \sin \theta d\theta \\ &= -\frac{\mu_0 nI}{2} \left[ -\cos \theta \right]_{\frac{3\pi}{4}}^{\frac{\pi}{4}} \\ &= -\frac{\mu_0 nI}{2} \left( -\cos \frac{\pi}{4} + \cos \frac{3\pi}{4} \right) \\ &= -\frac{\mu_0 nI}{2} \left( -\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}\right) \\ &= -\frac{\mu_0 nI}{2} \left( -\sqrt{2} \right) \\ &= \frac{\mu_0 nI}{\sqrt{2}}\\ \end{aligned}
よって答えは(ト)の\(\displaystyle \frac{\mu_0 nI}{\sqrt{2}}\)です。
無限長ソレノイドの軸上の磁束密度
無限長ソレノイドの時は(4)の式の積分範囲が\(\pi\)から0になります。
\begin{aligned} B_1 &= - \frac{\mu_0 n I}{2} \int_{\pi}^{0} \sin \theta d\theta \\ &= -\frac{\mu_0 nI}{2} \left[ -\cos \theta \right]_{\pi}^{0} \\ &= \mu_0 nI\\ \end{aligned}
よって答えは(ホ)の\(\mu_0 nI\)です。
無限長ソレノイドの磁束密度は他の問題でも出てくるため暗記しておいた方がいいでしょう。
- (1)ロ \(\displaystyle \frac{\mu_0 I }{2} \frac{\sin^3 \theta}{a} \)
- (2)ワ \(0\)
- (3)ヘ \(-\displaystyle \frac{\mu_0 nI}{2}\sin\theta\)
- (4)ト \(\displaystyle \frac{\mu_0 nI}{\sqrt{2}}\)
- (5)ホ \(\mu_0 nI\)