電験一種 H29年 理論 問6
問6 次の文章は、直流電源と2端子対抵抗回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
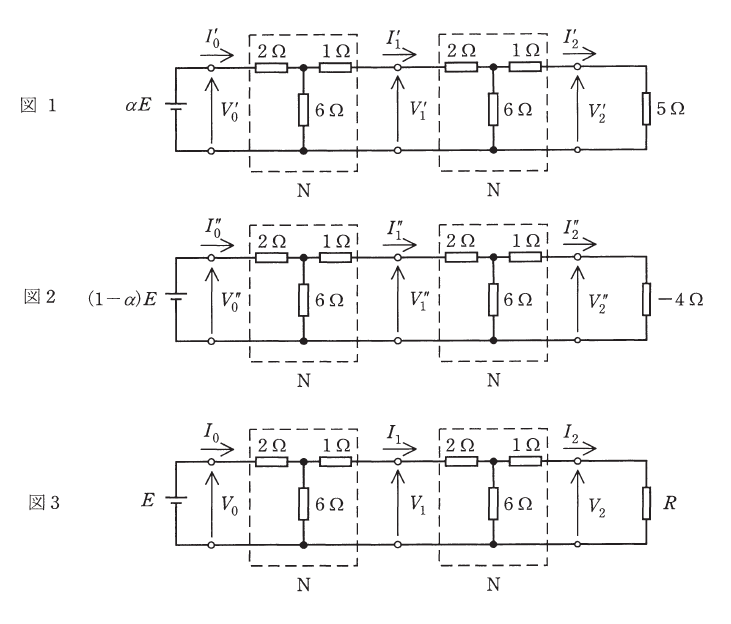
図のように、3種類の直流電圧源\(E\)、\((1-\alpha)E\)、\(\alpha E\)に同一の2端子対回路\(N\)を2段接続し、それぞれ異なる抵抗で終端した。図1, 図2の回路では、
\(\dfrac{V_0'}{I_0'} = \dfrac{V_1'}{I_1'} = \dfrac{V_2'}{I_2'} = 5\) Ω ,\(\dfrac{V_0''}{I_0''} = \dfrac{V_1''}{I_1''} = \dfrac{V_2''}{I_2''} = -4\) Ω \( \quad \cdots ①\)
が成立する。更に、分圧比、分流比の計算から、定数\(\lambda\)を用いて、①式の電圧、電流は、以下の等比数列で表すことができる。
\(V_k' = \lambda^{-k} \alpha E\), \(I_k' = \lambda^{-k} \dfrac{\alpha E}{5}\), \(k=0,1,2\)\( \quad \cdots ②\)
\(V_k'' = \lambda^{k} (1-\alpha)E\), \(I_k'' = -\lambda^{k} \dfrac{(1-\alpha)E}{4}\), \(k=0,1,2\)\( \quad \cdots ③\)
ここで、\(\lambda = \)(1)であり、\(\lambda\)とその逆数\(\lambda^{-1}\)は、図の2端子対回路\(N\)の(2)の固有値である。
次に図3の回路を解析する。任意の抵抗\(R\)に対し、図3の電圧\(V_k\)は図1の電圧\(V_k'\)と図2の電圧\(V_k''\)の和で、図3の電流\(I_k\)は図1の電流\(I_k'\)と図2の電流\(I_k''\)の和で、それぞれ表すことができる。
\(V_k = V_k' + V_k''\), \(I_k = I_k' + I_k''\), \(k=0,1,2\)\( \quad \cdots ④\)
ただし、\(\alpha\)は、図3の終端で④式の\(V_2\)と\(I_2\)が(3)の法則を満たす定数であり、\(\dfrac{V_2}{I_2} = \dfrac{V_2' + V_2''}{I_2' + I_2''} = R\)の式から一意に決定できる。例えば、\(R=0\) Ω(短絡)のときは、④式で\(V_2 = V_2' + V_2'' = 0\)となる。この式に\(\lambda = \)(1)と、\(k=2\)のときの②式及び③式を代入すると、\(\alpha = \)(4)を得る。これにより電流\(I_0\)は、\(I_0 = I_0' + I_0'' = \)(5) [A]となる。
なお、以上の解析法は、回路の段数が3段以上の場合にも適用できる。
| (イ) | \(\displaystyle \frac{15}{13}\) | (ロ)(3) | オーム | (ハ) | \(3\) | (ニ) | Z行列 |
| (ホ)(5) | \(\displaystyle \frac{23}{100}E\) | (ヘ) | ジュール | (ト) | \(4\) | (チ) | アンペール |
| (リ)(4) | \(\displaystyle \frac{16}{15}\) | (ヌ) | \(-\displaystyle \frac{13}{16}\) | (ル)(2) | F行列 | (ヲ) | \(\displaystyle \frac{19}{100}E\) |
| (ワ) | \(\displaystyle \frac{21}{100}E\) | (カ) | S行列 | (ヨ)(1) | \(2\) |
出典:平成29年度第一種電気主任技術者理論科目B問題問6
解説
過去問にないタイプの問題なためまず問題を理解するところで手間取ると思います。
このような問題は基本誘導である程度解けるようにはなっているので、冷静に読んで解ける問題を解ければ十分でしょう。(ただ理論は時間が足りなくなりがちなのでそれが難しいのですが)
定数\(\lambda\)
キルヒホッフの電圧則を左側の閉路に適用すると
\begin{aligned} V_0' &= 2 I_0' + 6(I_0' - I_1') \\ &= 8 I_0' - 6I_1' \\ \end{aligned}
が得られます。
ここに、問題にある\(V_k' = \lambda^{-k} \alpha E\)と\(I_k' = \lambda^{-k} \dfrac{\alpha E}{5}\)を代入すると、\( \lambda ^0 = 1\)なので
\begin{aligned} \alpha E & = 8 \left( \dfrac{ \alpha E}{5} \right) - 6 \left( \lambda^{-1} \dfrac{ \alpha E}{5} \right) \\ 1 &= \dfrac{ 8}{5} - \dfrac{ 6}{5 \lambda} \\ 5 &= 8 - \dfrac{ 6}{ \lambda} \\ -3 &= - \dfrac{ 6}{ \lambda} \\ \lambda &= 2 \\ \end{aligned}
となります。よって答えは(ヨ)の\(2\)です。
\(\lambda\)とその逆数\(\lambda^{-1} \)はなんの固有値か
\[\begin{pmatrix} V_1 \\ I_1 \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \end{pmatrix} \begin{pmatrix} V_2 \\ I_2 \end{pmatrix}\]
このように入力電圧・電流と出力電圧・電流の関係を記述する行列をF行列といいます。
固有値はさておき、行列の形がこれなので答えは(ル)のF行列です。
ちなみにZ行列の場合は以下のようになります。今回の形式にはあてはまりません。
\[\begin{pmatrix} V_1 \\ V_2 \end{pmatrix} = \begin{pmatrix} z_{11} & z_{12} \\ z_{21} & z_{22} \end{pmatrix} \begin{pmatrix} I_1 \\ I_2 \end{pmatrix}\]
また、S行列は過去問の選択肢としては出てこなかったと思います(定義としてS行列はある)。F行列を知らなければこれらから消去法で導くしかないかと思います。
試験中にやる必要はないですが、固有値は下記のようにして求められます。
\(\mathbf{E}\)は単位行列で\(\mathbf{F}\)はF行列です。
\[\det(\mathbf{F} - \lambda \mathbf{E}) = 0\]
行列の各パラメータを求めます。
2端子対回路Nは、図から直列インピーダンス\(Z_1 = 2\text{ }\Omega\)、並列アドミタンス\(Y_p = 1/6\text{ S}\)、直列インピーダンス\(Z_2 = 1\text{ }\Omega\)のT型回路と見ることができます。
T型回路のABCDパラメータは
\begin{aligned} A &= 1 + Z_1 Y_p \\ B &= Z_1 + Z_2 + Z_1 Z_2 Y_p \\ C &= Y_p \\ D &= 1 + Z_2 Y_p \\ \end{aligned}
で求められます。\(Z_1 = 2\), \(Z_2 = 1\), \(Y_p = 1/6\)なので、代入すると
\begin{aligned} A &= 1 + 2 \cdot \left( \dfrac{1}{6} \right) \\ &= 1 + \dfrac{1}{3} \\ &= \dfrac{4}{3} \\ B &= 2 + 1 + 2 \cdot 1 \cdot \left( \dfrac{1}{6} \right) \\ &= 3 + \dfrac{1}{3} \\ &= \dfrac{10}{3}\\ C &= \dfrac{1}{6} \\ D &= 1 + 1 \cdot \left( \dfrac{1}{6} \right)\\ &= \dfrac{7}{6} \\ \end{aligned}
よって、N回路のF行列は
\[\mathbf{F} = \begin{pmatrix} \dfrac{4}{3} & \dfrac{10}{3} \\ \dfrac{1}{6} & \dfrac{7}{6} \end{pmatrix}\]
となります。
\(\det \left( \mathbf{F} - \lambda \mathbf{E} \right) \)を計算します。
\begin{aligned} \det \left( \mathbf{F} - \lambda \mathbf{E} \right) &= \left( \dfrac{4}{3} - \lambda \right) \left( \dfrac{7}{6} - \lambda \right) - \left( \dfrac{10}{3} \right) \left( \dfrac{1}{6} \right) \\ &= \left(\dfrac{28}{18} - \dfrac{4}{3}\lambda - \dfrac{7}{6}\lambda + \lambda^2 \right) - \dfrac{10}{18} \\ &= \lambda^2 - \left(\dfrac{4}{3} + \dfrac{7}{6}\right)\lambda + \left(\dfrac{28}{18} - \dfrac{10}{18}\right) \\ &= \lambda^2 - \dfrac{15}{6} \lambda + \dfrac{18}{18} \\ &= \lambda^2 - \dfrac{5}{2} \lambda + 1 \\ \end{aligned}
これが0になればいいので
\begin{aligned} \lambda^2 - \dfrac{5}{2} \lambda + 1 &= 0 \\ 2\lambda^2 - 5 \lambda + 2 &= 0 \\ (2\lambda - 1)(\lambda - 2) &= 0 \\ \end{aligned}
したがって、固有値は、\(\lambda = \dfrac{1}{2}\) または \(\lambda = 2\)となります。
これは、(1)で求めた\(\lambda = 2\)と、その逆数\(\lambda^{-1} = 1/2\)に対応しており、F行列の固有値がこれらであることを示しています。
\(V_2\)と\(I_2\)が満たす法則
問題の中身の理解はさておき、選択肢としてはオームの法則以外は考えられないです。サービスでしょうか。
答えは(ロ)のオームです。
\(\alpha\)の値
\(R=0\) Ωの場合、終端は短絡されているため、終端電圧\(V_2\)は0になります
このとき、問題文に示されているように、\(V_2 = V_2' + V_2'' = 0\) という関係が成立します。
数値を代入すると以下のようになります。
\begin{aligned} V_2' + V_2'' &= 0 \\ \lambda^{-2} \alpha E + \lambda^{2} (1-\alpha)E &= 0 \\ \dfrac{1}{4}\alpha E + 4(1-\alpha)E &= 0 \end{aligned}
ここから\(\alpha\)を求めます。
\begin{aligned} 0 &= \dfrac{1}{4}\alpha + 4(1-\alpha)\\ 0 &= \alpha + 16 - 16\alpha \\ 15\alpha &= 16 \\ \alpha &= \dfrac{16}{15} \\ \end{aligned}
よって答えは(リ)の\(\displaystyle \frac{16}{15}\)です。
電流\(I_0\)
(4)で\(\alpha \)が求められたので、数字を代入して電流\(I_0\)を求めます。
まずは\( I_0'\)を求めます。
\begin{aligned} I_0' &= \lambda^{-0} \dfrac{\alpha E}{5} \\ &= \dfrac{\alpha E}{5} \\ &= \dfrac{16 E}{75} \end{aligned}
次に\(I_0''\)を求めます。
\begin{aligned} I_0'' &= -\lambda^{0} \dfrac{(1-\alpha)E}{4} \\ &= -\dfrac{(1-\alpha)E}{4} \\ &= -\dfrac{(1-\dfrac{16}{15})E}{4} \\ &= \dfrac{E}{60} \\ \end{aligned}
\(I_0\)はこれらの和なので
\begin{aligned} I_0 &= I_0' + I_0'' \\ &= \dfrac{16E}{75} + \dfrac{E}{60} \\ &= \dfrac{64E}{300} + \dfrac{5E}{300} \\ &= \dfrac{69E}{300} \\ &= \dfrac{23E}{100} \\ \end{aligned}
となります。よって答えは(ホ)の\(\displaystyle \frac{23}{100}E\)です。
- (1)ヨ \(2\)
- (2)ル F行列
- (3)ロ オーム
- (4)リ \(\displaystyle \frac{16}{15}\)
- (5)ホ \(\displaystyle \frac{23}{100}E\)