電験一種 H29年 理論 問5
次の文章は、三相交流回路に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
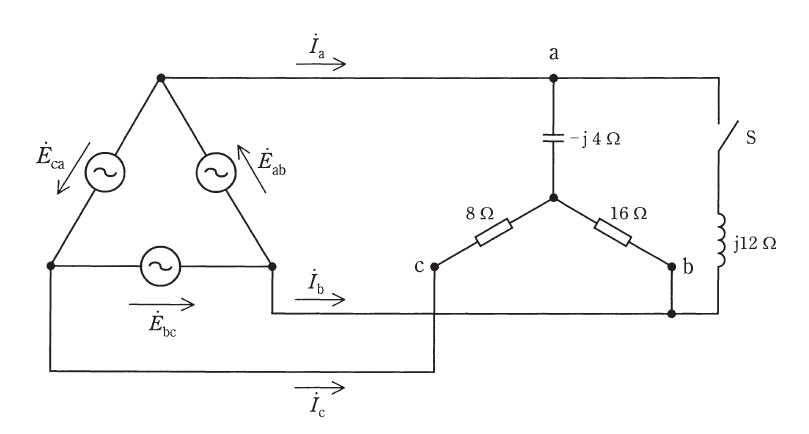
図のように、対称三相交流電源がY形不平衡負荷と12Ωの誘導性リアクタンスからなる回路に接続されている。図の各線間電圧は\(\dot{E}_{ab} = 100 \angle 0^\circ\) [V]を基準に、\(\dot{E}_{bc} = a^2 \dot{E}_{ab}\)、\(\dot{E}_{ca} = a \dot{E}_{ab}\)とする。ただし、\(a\)は複素数で\(a = e^{j \frac{2 \pi}{3}}\)である。
いま、スイッチSが開いている状態で線電流を求めると、\(\dot{I}_a = \)(1) A、\(\dot{I}_b = \)(2) A、\(\dot{I}_c = \)(3) Aとなる。また、負荷で消費される電力は(4) Wとなる。
次に、スイッチSを閉じ、12Ωの誘導性リアクタンスが端子a-b間に並列に接続されたとすると、線電流\(\dot{I}_a\)は\(\dot{I}_a = \)(5) Aとなる。
| (イ) | \(2800\) | (ロ) | \(5.20 - j1.41\) | (ハ) | \(-11.68 - j4.23\) |
| (ニ)(3) | \(-6.71 + j4.23\) | (ホ)(5) | \(13.20 - j9.26\) | (ヘ)(1) | \(13.20 - j0.93\) |
| (ト) | \(5.20 + j6.92\) | (チ) | \(11.68 + j1.41\) | (リ)(2) | \(-6.48 - j3.30\) |
| (ヌ)(4) | \(1350\) | (ル) | \(-5.20 - j6.92\) | (ヲ) | \(-1.52 - j3.30\) |
| (ワ) | \(-6.71 + j3.62\) | (カ) | \(1.52 + j2.70\) | (ヨ) | \(950\) |
出典:平成29年度第一種電気主任技術者理論科目B問題問5
解説
Y-Δ変換するよりそのまま計算した方が個人的には楽かと思ってます。好みの問題ですが。
ここではそのまま解きます。
線電流\(\dot{I_a}\)
画像のような閉回路を3つ考えます。また、\(\dot{I_a} + \dot{I_b} + \dot{I_c} = 0\)です。
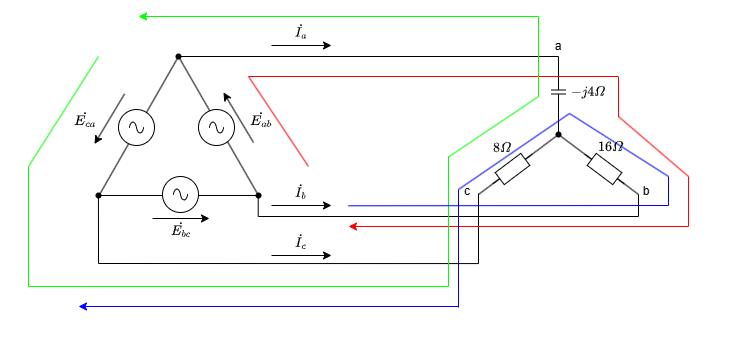
以下が成り立ちます。
\begin{aligned} \dot{E}_{ab} &= -j4\dot{I}_a - 16\dot{I}_b \\ a^2\dot{E}_{ab} &= 16\dot{I}_b - 8\dot{I}_c \\ a\dot{E}_{ab} &= 8\dot{I}_c - (-j4\dot{I}_a) \\ 0 &= \dot{I_a} + \dot{I_b} + \dot{I_c} \\ \end{aligned}
これを整理して\(\dot{I_a}\)、\( \dot{I_b} \)、\( \dot{I_c}\)を求めていきます。\(\dot{E}_{ab} = 100\)なので、
\begin{aligned} 100 &= -j4\dot{I}_a - 16\dot{I}_b \\ 100a^2 &= 16\dot{I}_b - 8\dot{I}_c \\ 100a &= 8\dot{I}_c + j4\dot{I}_a \\ 0 &= \dot{I_a} + \dot{I_b} + \dot{I_c} \\ \end{aligned}
\( \dot{I_c} = -\dot{I_a} - \dot{I_b} \)を用いて2番目の式より\(I_c\)を消去します。
\begin{aligned} 100a^2 &= 16\dot{I}_b - 8(-\dot{I}_a - \dot{I}_b)\\ &= 16\dot{I}_b + 8\dot{I}_a + 8\dot{I}_b\\ &= 8\dot{I}_a + 24\dot{I}_b \\ \end{aligned}
連立方程式を解いて\(\dot{I_a}\)を求めます。
\begin{aligned} \left\{ \begin{array}{l} 100 &= -j4\dot{I}_a - 16\dot{I}_b\\ 100a^2 &= 8\dot{I}_a + 24\dot{I}_b\\ \end{array} \right. \\ \left\{ \begin{array}{l} 300 &= -j12\dot{I}_a - 48\dot{I}_b \\ 200a^2 &= 16\dot{I}_a + 48\dot{I}_b \\ \end{array} \right. \\ \end{aligned}
\(\dot{I_b}\)を消去すると
\begin{aligned} 300 + 200a^2 &= (16 - j12)\dot{I}_a \\ 100(3 + 2a^2) &= 4(4 - j3 ) \dot{I}_a \\ 25(3 + 2a^2) &= (4 - j3 ) \dot{I}_a \\ 25(3 + 2a^2)(4 + j3 ) &= (4 - j3 )(4 + j3 ) \dot{I}_a \\ 25(3 + 2a^2)(4 + j3 ) &= 25 \dot{I}_a \\ (3 + 2a^2)(4 + j3 ) &= \dot{I}_a \\ \end{aligned}
\(\dot{I}_a\)からベクトルオペレータを消去すると
\begin{aligned} \dot{I}_a &= (3 + 2a^2)(4 + j3 ) \\ &= (3 - 1 - j\sqrt{3})(4 + j3 ) \\ &= (2 - j\sqrt{3})(4 + j3 ) \\ &= 8 + j6 - j4\sqrt{3} + 3\sqrt{3} \\ &= (8 + 3\sqrt{3}) + j(6 - 4\sqrt{3}) \\ &\fallingdotseq 13.196 - j0.928 \\ \end{aligned}
よって答えは(ヘ)の\(13.20 - j0.93\)です。
線電流\(\dot{I_b}\)
\( 100 = -j4\dot{I}_a - 16\dot{I}_b \)に(1)で求めた\(\dot{I_a}\)を代入して\(\dot{I_b}\)を求めます。
\begin{aligned} 100 &= -j4\dot{I}_a - 16\dot{I}_b \\ 25 &= -j\dot{I}_a - 4\dot{I}_b \\ 25 &= -j\left\{ (8 + 3\sqrt{3}) + j(6 - 4\sqrt{3})\right\} - 4\dot{I}_b \\ 25 &= 6 - 4\sqrt{3} -j(8 + 3\sqrt{3}) - 4\dot{I}_b \\ 4\dot{I}_b &= 6 -25 -4\sqrt{3} -j(8 + 3\sqrt{3}) \\ \dot{I}_b &= \frac{-19 - 4\sqrt{3}}{4} - j\frac{8 + 3\sqrt{3}}{4} \\ &\fallingdotseq -6.482 - j3.299 \\ \end{aligned}
よって答えは(リ)の\(-6.48 - j3.30\)です。
線電流\(\dot{I_c}\)
\( \dot{I_c} = -\dot{I_a} - \dot{I_b} \)で求めるのが楽でしょう。ただ、過去問を解く際は練習のために\(a\dot{E}_{ab}\)の式から求めてもいいかと思います。
\begin{aligned} \dot{I_c} &= -\dot{I_a} - \dot{I_b} \\ &\fallingdotseq -(13.196 - j0.928) - (-6.482 - j3.299 ) \\ &\fallingdotseq -6.714 + j4.227 \\ \end{aligned}
よって答えは(ニ)の\(-6.71 + j4.23\)です。
負荷で消費される電力
負荷で消費される電力\(P\)は、16Ωと8Ωの抵抗で消費される電力になるため
\begin{aligned} P &= 16|\dot{I}_b|^2 + 8|\dot{I}_c|^2 \\ &= 16 \left\{ (-6.482)^2 + (-3.299)^2 \right\} + 8 \left\{ (-6.714)^2 + (4.227)^2 \right\} \\ &= 16 \times 52.899725 + 8 \times 62.945425 \\ &= 1349.959 \end{aligned}
よって答えは(ヌ)の\(1350\)です。
誘導性リアクタンスが並列に接続された時の線電流\(\dot{I_a}\)
この場合、(1)で求めた電流(\(\dot{I_{a0}}\)とする)に\(\dot{I_{a}'} = \dfrac{\dot{E_{ab}}}{j12}\)が加えられた形となるので、
\begin{aligned} \dot{I_a} &= \dot{I_{a0}} + \dot{I_{a}'}\\ &\fallingdotseq 13.196 - j0.928 + \dfrac{100}{j12} \\ &\fallingdotseq 13.196 - j9.261 \\ \end{aligned}
よって答えは(ホ)の\(13.20 - j9.26\)です。
- (1)ヘ \(13.20 - j0.93\)
- (2)リ \(-6.48 - j3.30\)
- (3)ニ \(-6.71 + j4.23\)
- (4)ヌ \(1350\)
- (5)ホ \(13.20 - j9.26\)