電験一種 H29年 理論 問4
次の文章は、半導体に光を照射した際に生じる電気伝導に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
長さ\(L\)の真性半導体試料に、上方から光を均一に照射したところ、場所によらず均一に、単位時間、単位体積当たり\(g\)個の電子-正孔対が生成した。ここで試料の厚さは十分薄く、光吸収に伴う厚さ方向の電子-正孔対密度の変化は無視できるものとする。
いま、熱平衡状態における試料の電子密度を\(n_0\)、正孔密度を\(p_0\)とし、光照射により生成した電子密度の増加分を\(\Delta n\)、正孔密度の増加分を\(\Delta p\)とするとき、\(\Delta n\)と\(\Delta p\)の大きさの関係を式で表すと、(1)である。光照射により生成した電子のうち、単位時間、単位体積当たり\(\dfrac{\Delta n}{\tau}\)個が正孔と再結合して消滅する場合を考える。この\(\tau\)は再結合までの時間の目安であり、(2)と呼ばれる。定常状態では電子-正孔対の生成と消滅の割合は釣り合うことから、\(\Delta n = \)(3)となる。
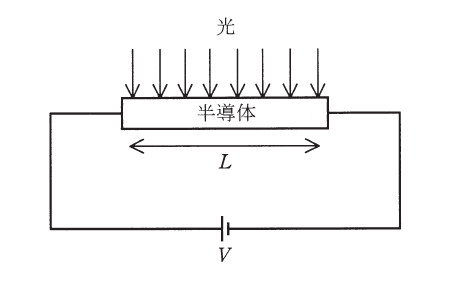
ここで図のように半導体試料の両端に電極を取り付け、電圧\(V\)を印加する。このとき、試料中には長さ方向に一様な電界\(E = \)(4)が発生し、電子と正孔は電界\(E\)からの力を受けて定常状態に達すると、\(E\)に比例したそれぞれ一定の平均速度で運動する。この比例係数を電子、正孔についてそれぞれ\(\mu_e\)、\(\mu_h\)とし、正孔の電荷量を\(q\)とすると、この運動による電流密度を計算することができる。光照射時の電流密度から、光を照射していないときの電流密度を差し引いて、光生成キャリアのみによる電流密度の大きさを求めると、(5)となる。これは、太陽電池や光検出器の基本原理として広く応用されている。
| (イ) | \(\displaystyle \frac{q\tau gV(\mu_h - \mu_e)}{L}\) | (ロ)(2) | キャリア寿命 | (ハ) | \(\displaystyle \frac{g}{\tau}\) |
| (ニ) | \(\Delta n\Delta p = n_0 p_0\) | (ホ) | \(\displaystyle \frac{V}{2L}\) | (ヘ)(4) | \(\displaystyle \frac{V}{L}\) |
| (ト) | 緩和時間 | (チ) | \(\Delta n\Delta p = (n_0+p_0)\sqrt{n_0 p_0}\) | (リ) | \(\displaystyle \frac{1}{\tau g}\) |
| (ヌ) | \(\displaystyle \frac{2V}{L}\) | (ル)(5) | \(\displaystyle \frac{q\tau gV(\mu_h + \mu_e)}{L}\) | (ヲ) | 回復時間 |
| (ワ)(1) | \(\Delta n = \Delta p\) | (カ)(3) | \(\tau g\) | (ヨ) | \(\displaystyle \frac{q\tau gV(\mu_h - \mu_e)}{2L}\) |
出典:平成29年度第一種電気主任技術者理論科目A問題問4
解説
仮に問題の意味が分からなかったとしてももっともらしい選択肢を選べるようになることが重要かと思います。
\(\Delta n\)と\(\Delta p\)の大きさの関係
真性半導体資料に均一に電子-正孔対が発生したと問題にあります。
これは励起後も等しいため、電子-正孔対は同じだけ生成されることになります。
よって答えは(ワ)の\(\Delta n = \Delta p\)です。
再結合までの時間の目安\(\tau\)
励起されたキャリアが再結合して消滅するまでの時間をキャリア寿命といいます。
よって答えは(ロ)のキャリア寿命です。
電子の増加分\(\Delta n\)を表す式
問題文にあるとおり、定常状態では電子-正孔対の生成と消滅の割合は釣り合うことから
\begin{aligned} \dfrac{\Delta n}{\tau} &= g \\ \Delta n &= \tau g \\ \end{aligned}
となるので答えは(カ)の\(\tau g\)です。
なお、gが単位時間、単位体積あたりの個数であること、\(\dfrac{\Delta n}{\tau}\)が単位時間、単位体積あたりの個数であり、\(\Delta n\)が個数であることを考えると\(\tau g\)以外単位が合いませんのでこれで答えを出してもいいかと思います。
試料中に発生する一様な電界\(E\)
サービス問題にあたるかと思います。
答えは(ヘ)の\(\displaystyle \frac{V}{L}\)です。
光生成キャリアのみによる電流密度の大きさ
正孔と電子がそれぞれ電流密度に寄与します。
正孔と電子の速度は移動度と電界の積で表されます。また、電流密度は電荷量と密度と速度の積になります。これらをまとめると、電流密度\(J\)は
\begin{aligned} J= \frac{q\tau gV(\mu_h + \mu_e)}{L} \\ \end{aligned}
となりますので、答えは(ル)の\(\displaystyle \frac{q\tau gV(\mu_h + \mu_e)}{L}\)です。
なお、他の選択肢は移動度が正孔と電子で同じような値の時に電流密度が0になってしまう、という考えで消去法で解いてもいいかと思います。
- (1)ワ \(\Delta n = \Delta p\)
- (2)ロ キャリア寿命
- (3)カ \(\tau g\)
- (4)ヘ \(\displaystyle \frac{V}{L}\)
- (5)ル \(\displaystyle \frac{q\tau gV(\mu_h + \mu_e)}{L}\)