電験一種 H29年 理論 問3
次の文章は、回路の過渡現象に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。
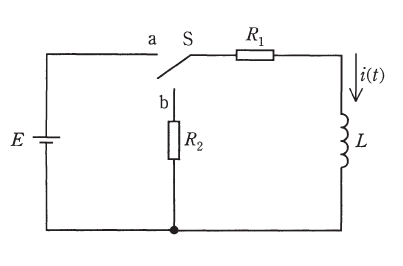
図の回路において、時刻\(t \lt 0\)では、スイッチSはa側にあり、回路は定常状態にあるものとする。
時刻\(t = 0\)で、スイッチSをb側に切り換えたとする。時刻\(t \geqq 0\)において、キルヒホッフの電圧則に従う微分方程式が成立するが、この微分方程式の両辺をラプラス変換し、コイル\(L\)を流れる電流\(I(s) = \mathcal{L}[i(t)]\)を求めると、
\(I(s) = \)(1)\( i(0) \quad \cdots ① \)
となる。ここで、\(i(0)\)は時刻\(t=0\)におけるコイルの電流であり、
\(i(0) = \)(2)\(\quad \cdots ② \)
で与えられる。
ラプラス逆変換により、時刻\(t \geqq 0\)における電流\(i(t)\)は、
\(i(t) = \mathcal{L}^{-1}[I(s)] = \)(3)\(\quad \cdots ③ \)
となる。
一方、\(t = \infty\)における電流\(i(\infty)\)は、①式及び②式で求めた\(I(s)\)にラプラス変換の最終値定理を適用すれば、
\(i(\infty) = \)(4)\(\quad \cdots ④ \)
と表される。
また、スイッチSをb側に切り換えた後に、\(t = \infty\)までに抵抗\(R_1\)で消費されるエネルギー\(W\)は、
\(W = \)(5)\(\quad \cdots ⑤ \)
となる。
| (イ) | \(\displaystyle \frac{E}{R_1+R_2}\) | (ロ)(1) | \(\displaystyle \frac{L}{sL+R_1+R_2}\) | (ハ) | \(\displaystyle \lim_{s\to\infty} \frac{sLE}{sR_1L+R_1(R_1+R_2)}\) |
| (ニ)(2) | \(\displaystyle \frac{E}{R_1}\) | (ホ) | \(\displaystyle \frac{E}{R_2}\) | (ヘ) | \(\displaystyle \frac{E}{R_1+R_2}e^{-\frac{R_1+R_2}{L}t}\) |
| (ト) | \(\displaystyle \frac{L}{sL+R_2}\) | (チ) | \(\displaystyle \frac{L}{sL+R_1}\) | (リ)(4) | \(\displaystyle \lim_{s\to 0} \frac{sLE}{sR_1L+R_1(R_1+R_2)}\) |
| (ヌ) | \(\displaystyle \frac{E}{R_2}e^{-\frac{R_1+R_2}{L}t}\) | (ル) | \(\displaystyle \frac{E^2}{2(R_1+R_2)}\) | (ヲ) | \(\displaystyle \lim_{s\to\infty} \frac{LE}{s^2R_1L+sR_1(R_1+R_2)}\) |
| (ワ)(5) | \(\displaystyle \frac{LE^2}{2R_1(R_1+R_2)}\) | (カ)(3) | \(\displaystyle \frac{E}{R_1}e^{-\frac{R_1+R_2}{L}t}\) | (ヨ) | \(\displaystyle \frac{LE^2}{2R_2(R_1+R_2)}\) |
出典:平成29年度第一種電気主任技術者理論科目A問題問3
解説
過渡現象は素直に解ける問題が多く得点源になるので確実に解けるようにしておきたいです。
コイル\(L\)を流れる電流\(I(s)\)
回路方程式は以下のようになります。
\[ L\frac{di(t)}{dt} + (R_1 + R_2)i(t) = 0 \]
これをラプラス変換して整理します。
\begin{aligned} \mathcal{L}\left[L\frac{di(t)}{dt} + (R_1 + R_2)i(t)\right] &= \mathcal{L}[0] \\ L[sI(s) - i(0)] + (R_1 + R_2)I(s) &= 0 \\ (sL + R_1 + R_2)I(s) &= Li(0) \\ I(s) &= \frac{L}{sL + R_1 + R_2}i(0) \\ \end{aligned}
よって答えは(ロ)の\(\displaystyle \frac{L}{sL+R_1+R_2}\)です。
時刻\(t=0\)におけるコイルの電流\(i(0)\)
\(i(0)\)の時の電流は、スイッチを切り換える前の定常状態においてコイルは短絡状態とみなせることから
\(i(0)=\dfrac{E}{R_1}\)
となります。よって答えは(ニ)の\(\displaystyle \frac{E}{R_1}\)です。
ラプラス逆変換による時刻\(t \geqq 0\)における電流\(i(t)\)
ラプラス逆変換\(\mathcal{L}^{-1}\left[\dfrac{1}{s+a}\right] = e^{-at}\)を使用します。
\begin{aligned} I(s) &= \frac{L}{sL + R_1 + R_2}i(0) \\ &= \frac{1}{s + \dfrac{R_1 + R_2}{L}}i(0) \\ \end{aligned} \begin{aligned} i(t) &= \mathcal{L}^{-1}\left[I(s)\right] \\ &= i(0) e^{-\frac{R_1 + R_2}{L}t}\\ &= \frac{E}{R_1} e^{-\frac{R_1 + R_2}{L}t} \\ \end{aligned}
よって答えは(カ)の\(\displaystyle \frac{E}{R_1}e^{-\frac{R_1+R_2}{L}t}\)です。
\(t = \infty\)における電流\(i(\infty)\)
ラプラスの最終値の定理\(\displaystyle f(\infty) = \lim_{s \to 0} sF(s)\)より
\begin{aligned} \lim_{s \to 0} sI(s) &= \frac{sL}{sL + R_1 + R_2}i(0) \\ &= \frac{sLE}{sR_1 L + R_1(R_1 + R_2)} \\ \end{aligned}
よって答えは(リ)の\(\displaystyle \lim_{s\to 0} \frac{sLE}{sR_1L+R_1(R_1+R_2)}\)です。
当然ですが、電源が繋がっていないため最終的に電流は0になります。
\(t = \infty\)までに抵抗\(R_1\)で消費されるエネルギー\(W\)
抵抗\(R_1\)の電力を\(t=\infty \)まで積分します。
\begin{aligned} W &= \int_0^\infty R_1 i(t)^2 dt \\ &= \frac{E^2}{R_1} \int_0^\infty e^{-\frac{2(R_1+R_2)}{L}t} dt \\ &= \frac{E^2}{R_1} \left\{ -\frac{L}{2(R_1 + R_2)} \right\} \left[ e^{-\frac{2(R_1+R_2)}{L}t} \right]_0^\infty \\ &= -\frac{LE^2}{2R_1(R_1 + R_2)} \left[ e^{-\frac{2(R_1+R_2)}{L}t} \right]_0^\infty \\ &= \frac{LE^2}{2R_1(R_1 + R_2)} \\ \end{aligned}
よって答えは(ワ)の\(\displaystyle \frac{LE^2}{2R_1(R_1+R_2)}\)です。
なお、コイルに蓄えているエネルギー\( \dfrac{1}{2} L i^2(0) = \dfrac{LE^2}{2R_1^2} \)以外のエネルギーが存在しないため、これが\(R_1\)と\(R_2\)でそれぞれ消費されると考えることもできます。この場合
\begin{aligned} W &= \dfrac{LE^2}{2R_1^2} \times \dfrac{R_1}{R1 + R_2} \\ &= \frac{LE^2}{2R_1(R_1 + R_2)} \\ \end{aligned}
となります。
- (1)ロ \(\displaystyle \frac{L}{sL+R_1+R_2}\)
- (2)ニ \(\displaystyle \frac{E}{R_1}\)
- (3)カ \(\displaystyle \frac{E}{R_1}e^{-\frac{R_1+R_2}{L}t}\)
- (4)リ \(\displaystyle \lim_{s\to 0} \frac{sLE}{sR_1L+R_1(R_1+R_2)}\)
- (5)ワ \(\displaystyle \frac{LE^2}{2R_1(R_1+R_2)}\)