電験一種 H29年 理論 問2
次の文章は、同軸円筒中の電界に関する記述である。文中の(0)に当てはまる最も適切なものを解答群の中から選べ。なお、円筒の端部が電界に及ぼす効果は無視できるものとする。
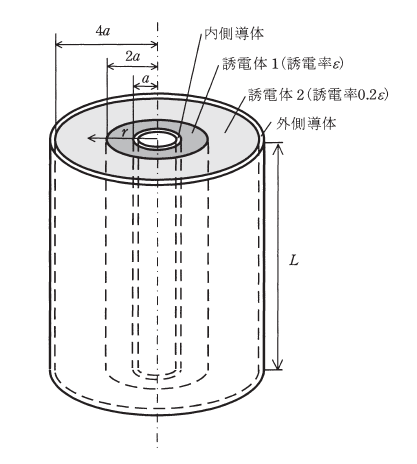
図のような長さ\(L\)、外半径\(a\)の内側導体と、長さ\(L\)、内半径\(4a\)の外側導体が中心軸を同じくして配置され、同軸円筒を構成している。内側導体と外側導体の間の空間は、図のように半径\(2a\)を境に、誘電率\(\varepsilon\)の誘電体1と誘電率\(0.2\varepsilon\)の誘電体2で満たされている。
このような誘電体の内部には、径方向の電界のみが発生する。内側導体に正の電荷\(+Q\)、外側導体に負の電荷\(-Q\)を与えた場合の誘電体内部の電界分布を、円筒状の閉曲面にガウスの法則を適用して求めると、誘電体1の内部の電界の大きさは\(E_1 = \)(1)、誘電体2の内部の電界の大きさは\(E_2 = \)(2)と表され、電界の大きさが最大となるのは、(3)である。
誘電体1の内側境界に対する外側境界の電位\(V_1\)は、電界を半径\(r\)方向に積分して、\(\displaystyle V_1 = -\int_a^{2a} E_1 dr = \)(4)と求められる。同様に、誘電体2の内側境界に対する外側境界の電位\(V_2\)を求めると\(V_2=5V_1\)となるので、この同軸円筒状の導体及び誘電体全体をコンデンサとみなしたときの容量は(5)と求められる。
| (イ) | \(\displaystyle -\frac{Qa}{2\pi \varepsilon L}\) | (ロ) | \(\displaystyle \frac{5Q}{2\pi \varepsilon L}\) | (ハ)(5) | \(\displaystyle \frac{\pi\varepsilon L}{3\ln2}\) |
| (ニ)(3) | 誘電体1と誘電体2の境界 | (ホ) | \(\displaystyle \frac{Q}{2\pi \varepsilon L}\) | (ヘ)(4) | \(\displaystyle -\frac{Q}{2\pi \varepsilon L}\ln2\) |
| (ト) | 誘電体2と外側導体の境界 | (チ) | \(\displaystyle \frac{5Q}{4\pi \varepsilon L} \frac{1}{r^2}\) | (リ) | \(\displaystyle \frac{Q}{4\pi \varepsilon L} \frac{1}{r^2}\) |
| (ヌ) | 内側導体と誘電体1の境界 | (ル)(1) | \(\displaystyle \frac{Q}{2\pi \varepsilon L} \frac{1}{r}\) | (ヲ) | \(\displaystyle \frac{\pi\varepsilon L}{3a}\) |
| (ワ)(2) | \(\displaystyle \frac{5Q}{2\pi \varepsilon L} \frac{1}{r}\) | (カ) | \(\displaystyle -\frac{Q}{8\pi \varepsilon L} \frac{1}{a}\) | (ヨ) | \(\displaystyle \frac{16\pi\varepsilon L a}{7}\) |
出典:平成29年度第一種電気主任技術者理論科目A問題問2
解説
基本的な問題にあたるかと思います。
誘電体1の内部の電界の大きさ
問題文にある通り、電界は径方向のみに発生するため、側面のみ考えればいいことになります。
よって、ガウスの法則より、誘電体1の範囲(\(a \lt r \lt 2a\))の電界は
\begin{aligned} \int_S \mathbf{E}_1 \cdot d\mathbf{S} &= 2\pi rLE_1 \\ &= \frac{Q}{\varepsilon} \\ \end{aligned} \begin{aligned} E_1 = \frac{Q}{2\pi \varepsilon L} \frac{1}{r} \\ \end{aligned}
となります。よって答えは(ル)の\(\displaystyle \frac{Q}{2\pi \varepsilon L} \frac{1}{r}\)です。
誘電体2の内部の電界の大きさ
(1)と同様に考えると、誘電体2の範囲(\(2a \lt r \lt 4a\))の電界は、誘電率の違いを考慮すると
\begin{aligned} \int_S \mathbf{E}_2 \cdot d\mathbf{S} &= 2\pi rLE_2 \\ &= \frac{Q}{0.2\varepsilon} \\ \end{aligned} \begin{aligned} E_2 = \frac{5Q}{2\pi \varepsilon L} \frac{1}{r} \\ \end{aligned}
となります。よって答えは(ワ)の\(\displaystyle \frac{5Q}{2\pi \varepsilon L} \frac{1}{r}\)です。
電界の大きさが最大になるところ
電界は半径\(r\)に反比例しているので、電界が最大になるところは誘電体1の最も内側か誘電体2の最も内側のどちらかしかありえません。
どちらが大きいか\(r=a\)と\(r=2a\)を代入して計算してみます。
\begin{aligned} E_1 &= \frac{Q}{2\pi \varepsilon L} \frac{1}{r} \\ &= \frac{Q}{2\pi \varepsilon L} \frac{1}{a} \\ E_2 &= \frac{5Q}{2\pi \varepsilon L} \frac{1}{r} \\ &= \frac{5Q}{2\pi \varepsilon L} \frac{1}{2a} \\ \end{aligned}
\(E_2 \gt E_1 \)なので誘電体2の最も内側が電界の大きさが最大となります。
よって答えは(ニ)の誘電体1と誘電体2の境界となります。
誘電体1の内側境界に対する外側境界の電位\(V_1\)
問題に式が与えられていますのでそのまま計算します。
\begin{aligned} V_1 &= -\int_a^{2a} E_1 dr \\ &= -\frac{Q}{2\pi\varepsilon L}\int_a^{2a} \frac{1}{r}dr \\ &= -\frac{Q}{2\pi\varepsilon L} [\ln r]_a^{2a} \\ &= -\frac{Q}{2\pi\varepsilon L} \ln 2 \\ \end{aligned}
よって答えは(ヘ)の\(\displaystyle -\frac{Q}{2\pi \varepsilon L}\ln2\)です。
同軸円筒状の導体及び誘電体全体をコンデンサとみなしたときの容量
問題文に\(V_2 = 5V_1 \)が与えられています。
内側の外側に対する電位は\(V = V_1 + V_2 = 6V_1 = -\dfrac{3Q}{\pi\varepsilon L} \ln 2 \)となりますので、コンデンサの容量は\(Q=CV\)より
\begin{aligned} C &= \left| \frac{Q}{V} \right| \\ &= \dfrac{Q} {\dfrac{3Q}{\pi\varepsilon L} \ln 2 } \\ &= \dfrac{\pi\varepsilon L }{3\ln 2} \\ \end{aligned}
よって答えは(ハ)の\(\displaystyle \frac{\pi\varepsilon L}{3\ln2}\)です。
- (1)ル \(\displaystyle \frac{Q}{2\pi \varepsilon L} \frac{1}{r}\)
- (2)ワ \(\displaystyle \frac{5Q}{2\pi \varepsilon L} \frac{1}{r}\)
- (3)ニ 誘電体1と誘電体2の境界
- (4)ヘ \(\displaystyle -\frac{Q}{2\pi \varepsilon L}\ln2\)
- (5)ハ \(\displaystyle \frac{\pi\varepsilon L}{3\ln2}\)