電験一種 H28年 理論 問6
次の文章は, 分布定数回路に関する記述である。文中の(1) に当てはまる最も適切なものを解答群の中から選べ。
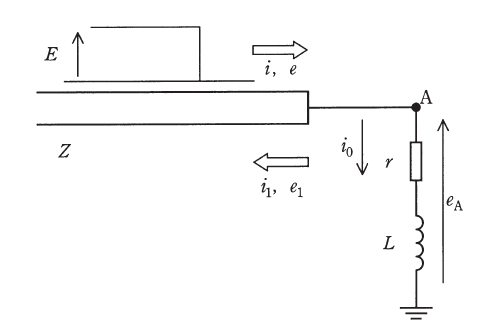
図のように特性インピーダンスが\(Z\)の半無限長無損失線路の終端\(A\)に, 負荷として抵抗\(r\)とインダクタンス\(L\)のコイルが接続されている。
波頭がステップ状で波高値\(E\)の電圧波\(e\)と, それに伴い波高値\(I\)の電流\(i\)が図の左側から終端\(A\)に向かって入射した。入射波は時刻\(t=0\)のとき終端\(A\)に達した。このときの終端\(A\)での電流\(i\)と反射による電流\(i_1\)及び負荷に流れる電流\(i_0\)との関係及び負荷の両端の電圧\(e_A\)を求めたい。電流\(i_1\), 電流\(i_0\)及び電圧\(e_A\), 終端\(A\)での反射により生じる電圧\(e_1\)を図のようににとる。電流は入射波が終端\(A\)に向かって進行する方向を正とする。
入射波到達後において, 終端\(A\)での電圧, 電流の関係は次式で表される。
\(e+e_1 = Zi+(-Zi_1) = e_A\)
\(i+i_1 = i_0\)
\(e_A\)と\(i_0\)の関係は次式で表される。
\(e_A = \) (1)
これらの式より, \(i_0\)の時間的変化を表す微少方程式が得られる。この式を初期値を考慮して解くと,
\(i_0 = \) (2)
となり, 時間的変化を表す図は (3) である。
また, \(e_A\)を\(E\)を用いて表すと次式となり,
\(e_A = \) (4)
その時間的変化を表す図は (5) である。
| (イ)(2) | \(\displaystyle \frac{2E}{r+Z}\left(1-e^{-\frac{r+Z}{L}t}\right)\) | (ロ) | \(\displaystyle \frac{2E}{r+Z}\left[r+Ze^{-(r+Z)Lt}\right]\) | (ハ)(1) | \(L\displaystyle \frac{di_0}{dt}+ri_0\) |
| (ニ) | \(2E\left(\displaystyle \frac{r}{Z}+e^{-\frac{r+Z}{L}t}\right)\) | (ホ)(4) | \(\displaystyle \frac{2E}{r+Z}\left(r+Ze^{-\frac{r+Z}{L}t}\right)\) | (ヘ) | \(L\displaystyle \frac{di_0}{dt}\) |
| (ト) | \(\displaystyle \frac{2E}{Z}\left(1-e^{-\frac{r+Z}{L}t}\right)\) | (チ) | \(\displaystyle \frac{2E}{r+Z}\left[1-e^{-(r+Z)Lt}\right]\) | (リ) | \(\displaystyle \frac{1}{L}\displaystyle \frac{di_0}{dt}+ri_0\) |
| (ヌ) | 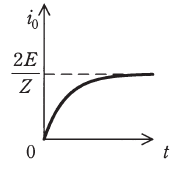 |
(ル)(3) | 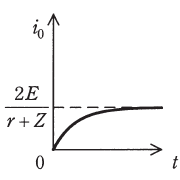 |
(ヲ) | 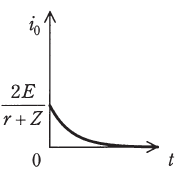 |
| (ワ)(5) | 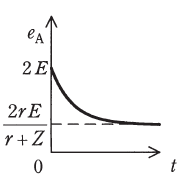 |
(カ) | 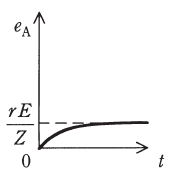 |
(ヨ) | 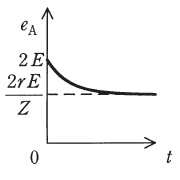 |
出典:平成28年度第一種電気主任技術者理論科目B問題問6
解説
分布定数回路は二次試験でも出るため考え方は難しいですがぜひ理解したい問題です。
\(e_A\)と\(i_0\)の関係
図より
\begin{aligned} e_A = L\frac{di_0}{dt} + ri_0 \\ \end{aligned}
よって答えは(ハ)の\(L\displaystyle \frac{di_0}{dt}+ri_0\)です。
\(i_0\)についての微分方程式を解いた結果
\(e_A = L\dfrac{di_0}{dt} + ri_0\)
この式より\(e_A\)を消去します。
問題にある通り、\(Zi + (-Zi_1) = e_A\)です。
また、\(i_1 = i_0 - i\)です。これらを代入すると
\begin{aligned} e_A &= L\dfrac{di_0}{dt} + ri_0\ \\ Zi -Zi_1 &= L\dfrac{di_0}{dt} + ri_0\ \\ Zi -Z(i_0 - i) &= L\dfrac{di_0}{dt} + ri_0\ \\ 2Zi &= L\dfrac{di_0}{dt} + (r+Z)i_0 \end{aligned}
となります。ここで、入射した電圧波は波高値\(E\)で電流は\(i\)とありますので、\(E= Zi\)を用いると
\begin{aligned} 2E &= L\dfrac{di_0}{dt} + (r+Z)i_0 \\ \end{aligned}
となります。後はこれを解きます。
ラプラス変換します。入射波は\(t=0\)の時に終端Aに達したとありますから、\(t=0\)の時、\(i_0 = 0\)です。
よって
\begin{aligned} \dfrac{2E}{s} &= sL I_0(s) + (r+Z)I_0(s) \\ I_0(s) &= \dfrac{2E}{s} \cdot \dfrac{1}{sL + r + Z } \\ \end{aligned}
部分分数分解します。
\begin{aligned} \dfrac{2E}{s} \cdot \dfrac{1}{sL + r + Z } &= \frac{A}{s} + \frac{B}{sL+r+Z} \\ 2E &= AsL + A(r+Z) + Bs \\ 2E &= (AL+B)s + A(r+Z) \\ \end{aligned}
係数を比較します。
\begin{aligned} A(r+Z) &= 2E \\ A &= \frac{2E}{r+Z} \\ \end{aligned}
\begin{aligned} AL + B &= 0 \\ B &= -AL \\ B &= -\frac{2EL}{r+Z} \\ \end{aligned}
よって、\(I_0(s)\)は
\begin{aligned} I_0(s) &= \frac{2E}{r+Z} \cdot \frac{1}{s} -\frac{2EL}{r+Z} \cdot \frac{1}{sL+r+Z} \\ &= \frac{2E}{r+Z} \left( \frac{1}{s} - \frac{1}{s+\dfrac{r+Z}{L}} \right) \end{aligned}
となります。これをラプラス逆変換すると
\begin{aligned} i_0 = \frac{2E}{r+Z}\left(1-e^{-\frac{r+Z}{L}t}\right) \\ \end{aligned}
となりますので、答えは(イ)の\(\displaystyle \frac{2E}{r+Z}\left(1-e^{-\frac{r+Z}{L}t}\right)\)です。
\(i_0\)の時間的変化の図
(2)の答えより、\(i_0\)は\(t=0\)の時\(0\)で時間の経過とともに\(\dfrac{2E}{r+Z}\)に近づいていきます。
これを表現している図は(ル)です。
\(e_A\)を\(E\)を用いて表す
(2)で\(i_0\)を求めているので、(1)の答えに代入し計算します。
\begin{aligned} e_A &= L\dfrac{di_0}{dt} + ri_0\ \\ &= L\dfrac{d}{dt}\left\{ \frac{2E}{r+Z}\left(1-e^{-\frac{r+Z}{L}t}\right) \right\} + r\left\{ \frac{2E}{r+Z}\left(1-e^{-\frac{r+Z}{L}t}\right)\ \right\} \\ &= \frac{2E\left(r+Z\right)}{r+Z} e^{-\frac{r+Z}{L}t} + \frac{2rE}{r+Z} - \frac{2rE}{r+Z} e^{-\frac{r+Z}{L}t} \\ &= \frac{2rE}{r+Z} + \frac{2ZE}{r+Z} e^{-\frac{r+Z}{L}t} \\ &= \frac{2E}{r+Z} \left( r + Ze^{-\frac{r+Z}{L}t} \right) \\ \end{aligned}
よって答えは(ホ)の\(\displaystyle \frac{2E}{r+Z}\left(r+Ze^{-\frac{r+Z}{L}t}\right)\)です。
\(e_A\)の時間的変化の図
(4)の答えより、\(t=0\)の時\(2E\)で時間の経過とともに\(\dfrac{2E}{r+Z}\)に近づくこと分かります。
これを表している図は(ワ)です。
- (1)ハ \(L\displaystyle \frac{di_0}{dt}+ri_0\)
- (2)イ \(\displaystyle \frac{2E}{r+Z}\left(1-e^{-\frac{r+Z}{L}t}\right)\)
- (3)ル

- (4)ホ \(\displaystyle \frac{2E}{r+Z}\left(r+Ze^{-\frac{r+Z}{L}t}\right)\)
- (5)ワ
